![]()
「ビッグバンを起こした陽子のラブの集団の引力と比重と、どのように原子はできたか。」
(この考えは、2015年6月12日に提出した、特願2015−119829.に記した)
1. ビッグバンをおこすための必要条件は何か。
・ビッグバンをおこした陽子のラブの自転軌道の比重はいくらか。
ビッグバンをおこした陽子のラブの自転軌道の比重は、1.3×1084です。
地表の陽子のラブの自転軌道の比重は、4.402×1022です。
ビッグバンをおこした陽子のラブの自転軌道の比重は、地表の陽子のラブの自転軌道の比重の、1.3×1084÷(4.402×1022)=2.953×1061倍、です。
この事については、2015年5月1日に提出した、特願2015−093867の「請求項3」に記した。
A=3.090×1020の場の陽子のラブと電子のラブの自転軌道の比重と地表の陽子のラブと電子のラブの自転軌道の比重
表1
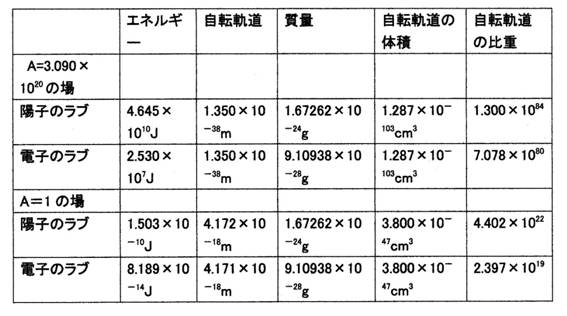
陽子のラブの自転軌道の比重の比
表2

参考
地表の陽子のラブの公転軌道の比重と電子のラブの公転軌道の比重はいくらか。
地表の陽子のラブの公転軌道は5.764×10−14mです。陽子のラブの質量は1.67265×10−27Kgです。
地表の陽子のラブの公転軌道の体積は、4/3×π(5.764×10−12cm÷2)3=4/3×π×(2.882×10−12cm)3=4/3×π×23.94×10−36cm3=1.002×10−34 cm3、です。
地表の陽子のラブの公転軌道の比重は、1.67265×10−24g÷(1.002×10−34 cm3)=1.669×1010、です。
地表の電子のラブの公転軌道は1.058×10−10mです。電子のラブの質量は9.1095×10−31Kgです。
地表の電子のラブの公転軌道の体積は、4/3×π(1.058×10−8cm÷2)3=4/3×π×(5.290×10−9cm)3=4/3×π×148.0×10−27 cm3=6.196×10−25 cm3
地表の電子のラブの公転軌道の比重は、質量÷体積=9.1095×10−28g÷(6.196×10−25 cm3)=1.470×10−3、です。
この事を表に示す。
地表の陽子のラブと地表の電子のラブの公転軌道の比重
表3

・ビッグバンをおこした場の引力はいくらか。
引力とは電子が1秒間に作り出す磁気の光子の軌道エネルギーです。この磁気の光子の軌道エネルギーは一定です。10−31Jmです。
A=3.090×1020の場合。
電子のラブの自転軌道=地表の電子のラブの自転軌道÷A=4.175×10−18m÷(3.090×1020)=1.351×10−38m
電子のラブのエネルギー=地表の電子のラブのエネルギー×A=8.187×10−14J×3.090×1020=2.530×107J
電子のラブが1秒間に作るエネルギー=3.083×10−33Jm÷自転軌道=3.083×10−33Jm÷(1.351×10−38m)=2.282×105J
電子が1秒間に作り出す磁気の光子の軌道エネルギー=電子のラブが1秒間に作るエネルギー×電子のラブの自転軌道=2.282×105J×1.351×10−38m=3.083×10−33Jm
ここで問題が発生しました。
A=3.090×1020の場合に於いて、電子が1秒間に作り出す磁気の光子の軌道エネルギーは3.083×10−33Jmです。これは地表の場合とほぼ同じです。
もしかしたら、引力は電子が1秒間に作り出す磁気の光子の軌道エネルギーではないのかもしれない。
○再度引力について考える。
2. 引力とは何か。
2005年5月10日に提出した、特願2005−166134の「請求項13」で、次のように記した。
万有引力定数は6.672×10−11Nmm/kg2ですから、1000gでできる万有引力は(6.672×10−11)1/2J=8.16×10−6Jです。1000gには、1000÷12×6.022×1023個=5×1025個の電子があります。1個の電子でできる万有引力は、8.16×10−6J÷(5×1025個)=1.63×10−31Jです。
2005年6月10日に提出した、特願2005−198056「中性子と素粒子2」では、ボーア磁子9.274×10−24J/T、核磁子5.0508×10−27J/Tから導き出された、電子のラブによってできた磁気の光子のエネルギーと運動量、陽子のラブによってできた磁気の光子のエネルギーと運動量の表では、軌道1mにおける、磁気の光子のエネルギー=万有引力=9.274×10−32Jm÷1m=9.274×10−32J。
それで、万有引力の式をもう1度考察する。
万有引力定数=6.672×10−11Nm2/Kg2
万有引力定数は6.672×10−11Nm2/Kg2ですから、1000gでできる万有引力は、(6.672×10−11 Nm2/Kg2)1/2=8.16×10−6 Nm/Kgです。1000gには、1000÷12×6.022×1023個=5×1025個の原子があります。アボガドロ数で算出しています。
1個の原子でできる万有引力は、8.16×10−6Nm÷(5×1025個)=1.63×10−31Nm=1.63×10−31Jです。
この式によって、1個の原子でできる万有引力は、1.63×10−31Jです。
私はいままで、引力は電子が1秒間に作り出す磁気の光子の軌道エネルギーであると考えてきたが、これは間違えです。
1個の原子でできる万有引力は、1公転で作る磁気の光子のエネルギーです。
この事を表に示す。
1個の原子でできる万有引力は、1公転で作る磁気の光子のエネルギー
表4

3. 1個の原子でできる万有引力は、1.63×10−31Jです。これはどのようなエネルギーであるか。
・ボーア磁子は9.274×10−24Jです。これは、7.96×107公転によりできた磁気の光子のエネルギーです。
1公転でできる磁気の光子のエネルギーは、9.274×10−24J÷(7.96×107公転)=1.165×10−31J、です。
即ち、1個の原子でできる万有引力は、1.63×10−31Jです。これは、電子のラブが1公転で作る磁気の光子のエネルギーです。
1公転には磁気の光子が7.96×107個存在します。
それで、磁気の光子1個のエネルギーは、1.165×10−31J÷(7.96×107個)=1.464×10−39J、です。
・核磁子は5.05×10−27Jです。これは、4.34×104公転によりできた磁気の光子のエネルギーです。
1公転でできる磁気の光子のエネルギーは、5.05×10−27J÷(4.34×104公転)=1.164×10−31J、です。
即ち、1個の原子でできる万有引力は、1.164×10−31Jです。これは、陽子のラブが1公転で作る磁気の光子のエネルギーです。
1公転には磁気の光子が4.34×104個存在します。
それで、磁気の光子1個のエネルギーは、1.164×10−31J÷(4.34×104個)=2.682×10−36J、です。
万有引力になる磁気の光子は、原子の外側の電子のラブが作る磁気の光子です。
この事をまとめて表に示す。
ボーア磁子から算出した電子のラブが1公転で作る引力に成る磁気の光子のエネルギーと核磁子から算出した陽子のラブが1公転で作る引力に成る磁気の光子のエネルギー
表5
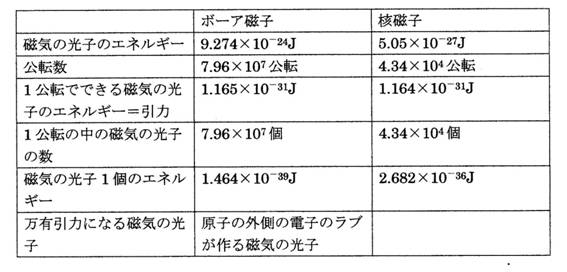
理解できた事。
1. 万有引力は、原子の外側の磁気の光子です。
2. 万有引力は、電子のラブが1公転で作る磁気の光子のエネルギーで、ボーア磁子÷公転数=9.274×10−24J÷(7.96×107公転)=1.165×10−31J、です。
3. 磁気の光子1個のエネルギーは、1.165×10−31J÷(7.96×107個)=1.464×10−39J、です。
4. 陽子のラブが作る引力は1公転で作る磁気の光子のエネルギーで、核磁子÷公転数=5.05×10−27J÷(4.34×104公転)=1.164×10−31J、です。
5. 原子では電子のラブが作る引力と陽子のラブが作る引力は、共に1.165×10−31Jであり、等しい。等しい引力で引き合っている。
4. ビッグバンをおこした陽子のラブの引力と陽子のラブの集団の引力はいくらか。
陽子のラブが1公転で作る磁気の光子のネルギー(引力)は、地表で、1.164×10−31Jです。
それで、ビッグバンをおこした陽子のラブの引力は、1.164×10−31J×ビッグバンの時のA=1.164×10−31J×3.090×1020=3.597×10−11J、です。
陽子のラブ集団の引力は、陽子のラブの引力×陽子のラブ集団の数=3.597×10−11J×2.674×1079個=9.618×1068J、です。
2011年6月23日に提出した、特願2011−139785に記したように、軌道エネルギーは素粒子の表面の数×素粒子が1秒間に作る光子のエネルギーであると考える場合。
・素粒子の表面の数はいくらか。
4π/3×r3=2.674×1079個。 r3=2.674×1079個÷4π/3=6.3871×1078。 r=6.3871/3×1026=1.855×1026(個)
素粒子の表面の数=4πr2=4π(1.855×1026個)2=4.322×1053個
素粒子の表面の数は4.322×1053個です。
陽子のラブ集団の表面の数は、4.322×1053個です。
それで、球体の表面の陽子のラブが作ったビッグバンをおこした陽子のラブの引力=陽子のラブ集団の表面の数×ビッグバンをおこした陽子のラブの引力=4.322×1053個×3.597×10−11J=1.555×1043J、です。
ビッグバンをおこした陽子のラブの引力と陽子のラブの集団の引力と陽子のラブの集団の表面の引力
表6

5. 放出した電磁気は1.657×10−18Jである場合、原子数はいくらか。
2010年12月2日に提出した、特願2010−269415に於いて、放出した電磁気は1.657×10−18Jであり、原子数は2.674×1079個であると次のように記した。
(電磁場の電磁気が集まった大きさは、電磁気の軌道×総合電磁気数1/3=5.5×107mで一定ですから、この式より原子数を求める。
電磁気の軌道×総合電磁気数1/3=5.5×107m
総合電磁気数1/3=5.5×107m÷電磁気の軌道=5.51×107m÷(4.648×10-62÷a2m)=5.51×107m÷{4.648×10-62÷(1.657×10-18J)2m}=5.51×107m÷(1.693×10-26m)=3.255×1033
総合電磁気数=(3.255×1033)3=3.449×10100(個)
総合電磁気数=1.290×1021×できる原子数=3.449×10100個
原子数=3.449×10100個÷(1.290×1021)=2.674×1079個
原子数は2.674×1079個であった)
今回は、できる宇宙の原子数=1.0765×1079×できる電子のラブのエネルギー6、の式により求める。(この式は2009年9月19日に提出した、特願2009−218192に記した)
放出した電磁気は1.657×10−18Jである場合、できる電子のラブのエネルギー=放出した電磁気×電子のラブの電磁気数=1.657×10−18J×7.0225×1017個=1.164J、です。
できる宇宙の原子数=1.0765×1079×できる電子のラブのエネルギー6=1.0765×1079×1.1646=1.0765×1079×2.487=2.678×1079
できる宇宙の原子数は、2.678×1079個です。
これは、特願2010−269415に於いて求めた原子数とほぼ同じであるので、原子数は2.674×1079個とする。
6. ビッグバンをおこしたときの陽子のラブの集団の体積と比重はいくらか。
・ビッグバンをおこしたときの陽子のラブの集団の総合質量はいくらか
ビッグバンをおこしたときの陽子のラブの集団の総合質量=陽子のラブの質量×陽子のラブの総数=1.67262×10−24g×2.674×1079個=4.473×1055g
・ビッグバンをおこしたときの陽子のラブの集団の体積と比重はいくらか。
半径にr個の陽子のラブが存在するとする。
4/3×πr3個=2.674×1079個
r3個=2.674×1079個÷(4/3×π)=6.387×1078
r=(6.387×1078)1/3=1.855×1026
半径に1.855×1026個の陽子のラブが存在する。
半径の長さ=陽子のラブの自転軌道×半径の陽子のラブの数=1.350×10−38m×1.855×1026個=2.504×10−12m=2.504×10−10cm
陽子のラブの集団の体積=4/3×π(2.504×10−10cm)3=4/3×π×1.570×10−29 cm3=6.573×10−29 cm3
陽子のラブの集団の比重=陽子のラブの集団の総合質量÷陽子のラブの集団の体積=4.473×1055g÷(6.573×10−29 cm3)=6.805×1083
ビッグバンをおこしたときの陽子のラブの集団の体積は6.573×10−29 cm3で、比重は6.805×1083、です。
これは陽子のラブの比重とほぼ等しい
まとめて表に示す。
ビッグバンの時の陽子のラブの集団の様子
表7

この事により理解できる事
1.陽子のラブの集団の引力は9.618×1068Jに成り、ビッグバンがおきた。
2.陽子のラブの集団の比重は6.805×1083に成り、ビッグバンがおきた。
7. 質量を作る場の必要条件は何か。
質量を作る場は最も自転軌道の比重が大きい場です。
質量を作る場の必要条件は陽子のラブの自転軌道の比重が1.300×1084であることです。
質量を作る場の必要条件は電子のラブの自転軌道の比重が7.078×1080であることです。
質量を作る場の必要条件はA=3.090×1020の場で、陽子のラブのエネルギーが4.645×1010Jであることです。
質量を作る場の必要条件はA=3.090×1020の場で、電子のラブのエネルギーが2.530×107Jであることです。
8. どうしてビッグバンは起きたか。
質量ができたからビッグバンは起きた。
比重が大きく成り、その比重を保ちきれなくなり爆発した。
陽子のラブの自転比重が1.3×1084となり、この比重を保ちきれなくなったので、爆発した。
陽子のラブの集団の比重が6.805×1083となり、この比重を保ちきれなくなったので、爆発した。
9. ビッグバンをおこした場の引力はいくらか。地表の引力の何倍か。
地表では、電子のラブが1公転で作る磁気の光子のエネルギーは、ボーア磁子÷公転数=9.274×10−24J÷(7.96×107公転)=1.165×10−31J、です。
このエネルギーが万有引力です。
ビッグバンをおこした場のAは、aJ=1.657×10−18Jの場合、A=3.090×1020ですから、電子のラブが7.96×107回の自転で作る磁気の光子のエネルギーは、
地表のエネルギー×3.090×1020=1.165×10−31J×3.090×1020=3.600×10ー11J、です。
ビッグバンをおこした場の電子のラブが作る磁気の光子のエネルギーは3.600×10ー11Jです。
中央の陽子のラブの集団の陽子のラブが1公転で作る磁気の光子のエネルギーは、核磁子÷公転数×A=5.05×10−27J÷(4.34×104公転)×3.090×1020=1.164×10−31J×3.090×1020=3.597×10−11J、です。
ビッグバンをおこした場の引力は、地表の引力の、3.597×10−11J÷(1.165×10−31J)=3.090×1020倍、です。
1原子と1原子の間の引力は、1原子でできる磁気の光子のエネルギー2÷1原子の直径2=1電子のラブが作る引力になる磁気の光子のエネルギー2÷1原子の直径2、です。
地表の原子と原子の間の引力=1原子でできる引力のエネルギー2÷電子のラブの公転軌道2=(1.165×10−31J)2÷(1.058×10−10m)2=1.212×10−42J/m 、です。
ビッグバンの以前、A=3.090×1020の場では、陽子のラブと陽子のラブの間の引力は、陽子のラブが作る引力のエネルギー2÷陽子のラブの自転軌道2=(1.165×10−31J×3.090×1020)2÷{地表の陽子のラブの自転軌道÷(3.090×1020)}2=(1.165×10−31J×3.090×1020)2÷{4.18×10−18m÷(3.090×1020)}2=(3.600×10−11)2÷(1.353×10−38m)2=1.296×10−21J÷(1.831×10−76m)=7.078×1054J/m、です。
A=3.090×1020の場の陽子のラブと陽子のラブの間の引力÷地表の原子と原子の間の引力=7.078×1054J/m÷(1.212×10−42J/m)=5.840×1096倍
A=3.090×1020の場の陽子のラブと陽子のラブの間の引力は地表の原子と原子の間の引力の5.840×1096倍です。
ビッグバンをおこした場の陽子のラブの引力は3.597×1011Jです。陽子のラブと陽子のラブの間の引力は7.067×1054J/mです。
地表の引力は1.165×10−31Jです。地表の1原子と1原子の間の引力は1.283×10−52J/m
ビッグバンをおこした場の引力は、地表の引力の、3.090×1020倍です。
地表の原子と原子の間の引力は、1.212×10−42J/mです。
ビッグバンをおこした場の陽子のラブと陽子のラブの間の引力は、7.078×1054J/mです。
ビッグバンをおこした場の陽子のラブと陽子のラブの間の引力は地表の原子と原子の間の引力の、5.840×1096倍です。
この事を表に示す。
地表の1原子と1原子の間の引力とビッグバンをおこした場の陽子のラブと陽子のラブの間の引力の比
表8
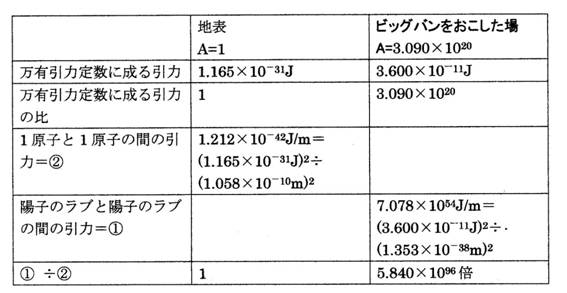
この事により理解できる事
1.Aの場の万有引力定数に成る引力は、1.165×10−31J×Aです。
2.ビッグバンをおこした場の陽子のラブと陽子のラブの間の引力は地表の1原子と1原子の間の引力の5.840×1096倍です。
3.ビッグバンをおこした場の陽子のラブと陽子のラブの間の引力が地表の1原子と1原子の間の引力の5.840×1096倍であることにより、爆発した。
4.陽子のラブと陽子のラブの間の引力が7.078×1054J/mであることにより、爆発した。
10. もし、宇宙の素粒子の中で原子に成ることができた物が4%であり、96%がダークマターであるとするなら、陽子のラブの集団の爆発により、どのように原子はできたか。
ビッグバンの以前、陽子のラブの集団ができた場の様子は、まるで太陽圏のようであった。中央に陽子のラブの集団があり、それを電子のラブの集団が地球のように回転していた。
この事により、陽子のラブの集団が爆発したとき、原子ができるのは、陽子のラブと電子のラブが衝突した数です。
・陽子のラブの集団の立方体の1辺の長さはいくらか。
陽子のラブの集団の立方体の1辺の長さ=陽子のラブの数1/3×陽子のラブの自転軌道=(2.674×1079個)1/3×1.350×10−38m=(26.74×1078個)1/3×1.350×10−38m=2.990×1026個×1.350×10−38m=4.037×10−12m
陽子のラブの集団の立方体の1辺の長さは、4.037×10−12mです。
・電子のラブの集団の立方体の1辺の長さはいくらか。
電子のラブの集団の立方体の1辺の長さ=電子のラブの数1/3×電子のラブの自転軌道=(2.674×1079個)1/3×1.350×10−38m=(26.74×1078個)1/3×1.350×10−38m=2.990×1026個×1.350×10−38m=4.037×10−12m
電子のラブの集団の立方体の1辺の長さは、4.037×10−12mです。
・陽子のラブの集団の球体の直径はいくらか。
半径rにr個の陽子のラブが存在するとする。
4/3×πr3=2.674×1079個
r3=2.674×1079個÷(4/3×π)=6.387×1078個
r=1.855×1026個
直径の陽子のラブの数=1.855×1026個×2=3.710×1026個
陽子のラブの集団の球体の直径=半径に存在する陽子のラブの数×2×陽子のラブの自転軌道=1.855×1026個×2×1.350×10−38m=5.009×10−12m
電子のラブの集団の球体の直径=半径に存在する電子のラブの数×2×電子のラブの自転軌道=1.855×1026個×2×1.350×10−38m=5.009×10−12m
陽子のラブの集団の立方体の1辺の長さと陽子のラブの集団の球体の直径
表9

・陽子のラブの集団と電子のラブの集団の間の距離はいくらか。
陽子のラブの集団の立方体の1辺の長さ=電子のラブの集団の立方体の1辺の長さ=4.037×10−12mとする場合。
陽子のラブの集団の立方体の1辺の長さ÷2=4.037×10−12m÷2=2.019×10−12m
陽子のラブの集団と電子のラブの集団の間の距離=陽子のラブの集団の1/2×1836=2.019×10−12m×1836=3.707×10−9m
陽子のラブの集団と電子のラブの集団の間の距離は、3.707×10−9mです。
・陽子のラブの集団と電子のラブの集団の間の距離は、3.707×10−9mで、電子のラブの集団の大きさは4.037×10−12mです。この場合全ての陽子のラブと電子のラブは質量をもっています。もし、宇宙の素粒子の中で原子に成ることができた物が4%であり、96%がダークマターであるとするなら、陽子のラブの内4%が電子のラブの集団に衝突し、原子に成った。
・半径3.707×10−9mの球体の表面積に陽子のラブは飛散した。そのうち4%の表面積に当たったものが原子に成った。4%の表面積はいくらか。
半径3.707×10−9mの球体の表面積=4π×(3.707×10−9m)2=1.726×10−16m2
半径3.707×10−9mの球体の表面積×0.04=4π×(3.707×10−9m)2×0.04=4π×13.74×10−18m2×0.04=6.903×10−18 m2
半径3.707×10−9mの球体の表面積の内6.903×10−18 m2に当たった陽子のラブが電子のラブと衝突し、原子に成った。
・6.903×10−18 m2の長さはいくらか。
6.903×10−18 m2の長さは、(6.903×10−18 m2)1/2=2.627×10-9m、です。
その場所は、電子のラブの集団が存在していた場所です。
電子のラブの集団の立方体の1辺の長さ=4.037×10−12mですから、その2.627×10-9m÷(4.037×10−12m)=6.508×102倍の長さです。
即ち、電子のラブの集団の大きさは、6.508×102倍に拡大し、それに、陽子のラブは衝突した。
・陽子のラブの集団と電子のラブの集団の間の距離はいくらか。
陽子のラブの集団の球体の直径=電子のラブの集団の球体の直径=5.009×10−12m。
陽子のラブの集団の球体の半径=陽子のラブの集団の球体の直径÷2=5.009×10−12m÷2=2.505×10−12m
陽子のラブの集団の球体と電子のラブの集団の球体の間の距離=陽子のラブの集団の球体の半径×1836=2.505×10−12m×1836=4.499×10−9m
陽子のラブの集団と電子のラブの集団の間の距離は、4.499×10−9mです。
・陽子のラブの集団と電子のラブの集団の間の距離は、4.499×10−9mで、電子のラブの集団の球体の直径は5.009×10−12mです。この場合全ての陽子のラブと電子のラブは質量をもっています。もし、宇宙の素粒子の中で原子に成ることができた物が4%であり、96%がダークマターであるとするなら、陽子のラブの内4%が電子のラブの集団に衝突し、原子に成った。
・半径4.499×10−9mの球体の表面積に陽子のラブは飛散した。そのうち4%の表面積に当たったものが原子に成った。4%の表面積はいくらか。
半径4.499×10−9mの球体の表面積=4π×(4.499×10−9m)2=2.542×10−16m2
半径4.499×10−9mの球体の表面積×0.04=2.542×10−16m2×0.04=1.017×10−17 m2
半径4.499×10−9mの球体の表面積の内1.017×10−17 m2に当たった陽子のラブが電子のラブと衝突し、原子に成った。
・1.017×10−17 m2の長さはいくらか。
1.017×10−17m2の長さは、(1.017×10−17 m2)1/2=3.189×10-9m、です。
その場所は、電子のラブの集団が存在していた場所です。
電子のラブの集団の球体の大きさ=5.009×10−12mですから、その3.189×10-9m÷(5.009×10−12m)=6.367×102倍の長さです。
即ち、電子のラブの集団の球体の大きさは、6.367×102倍に拡大し、それに、陽子のラブは衝突した。
陽子のラブの集団の立体の1辺の長さと、陽子のラブの集団の球体の直径の比較
表10
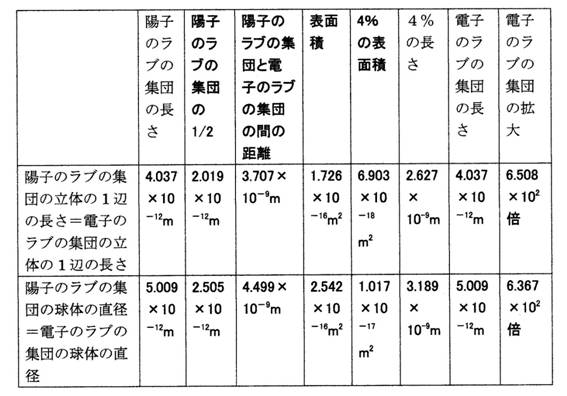
【図面の簡単な説明】
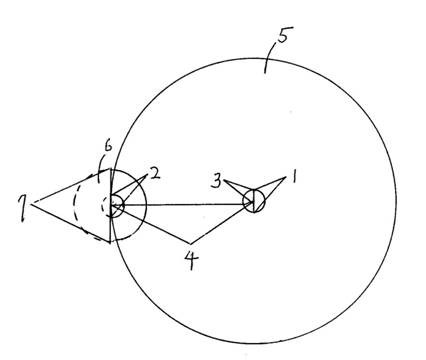
【図1】図1は、もし、宇宙の素粒子の中で原子に成ることができた物が4%であり、96%がダークマターであるとするなら、陽子のラブの集団の爆発により、どのように原子はできたかを図示する。
ビッグバンの以前、陽子のラブの集団ができた場の様子は、まるで太陽圏のようであった。中央に陽子のラブの集団があり、それを電子のラブの集団が地球のように回転していた。
この事により、陽子のラブの集団が爆発したとき、原子ができるのは、陽子のラブと電子のラブが衝突した数です。
・陽子のラブの集団の球体の直径はいくらか。
半径にr個の陽子のラブが存在するとする。
4/3×πr3=2.674×1079個。
r3=2.674×1079個÷(4/3×π)=6.387×1078個。
r=1.855×1026個。
半径の陽子のラブの数=1.855×1026個。
陽子のラブの集団の球体の直径1 =半径に存在する陽子のラブの数×2×陽子のラブの自転軌道=1.855×1026個×2×1.350×10−38m=5.009×10−12m。
電子のラブの集団の球体の直径2 =半径に存在する電子のラブの数×2×電子のラブの自転軌道=1.855×1026個×2×1.350×10−38m=5.009×10−12m。
陽子のラブの集団の球体の半径3 =陽子のラブの集団の球体の直径÷2=5.009×10−12m÷2=2.505×10−12m。
陽子のラブの集団の球体と電子のラブの集団の球体の間の距離4 =陽子のラブの集団の球体の半径×1836=2.505×10−12m×1836=4.499×10−9m。
陽子のラブの集団と電子のラブの集団の間の距離は、4.499×10−9mです。
・陽子のラブの集団と電子のラブの集団の間の距離は、4.499×10−9mで、電子のラブの集団の球体の直径は5.009×10−12mです。この場合全ての陽子のラブと電子のラブは質量をもっています。もし、宇宙の素粒子の中で原子に成ることができた物が4%であり、96%がダークマターであるとするなら、陽子のラブの内4%が電子のラブの集団に衝突し、原子に成った。
・半径4.499×10−9mの球体の表面積に陽子のラブは飛散した。そのうち4%の表面積に当たったものが原子に成った。4%の表面積はいくらか。
半径4.499×10−9mの球体の表面積5 =4π×(4.499×10−9m)2=2.542×10−16m2。
半径4.499×10−9mの球体の表面積×0.04 6 =2.542×10−16m2×0.04=1.017×10−17 m2。
半径4.499×10−9mの球体の表面積の内1.017×10−17 m2に当たった陽子のラブが電子のラブと衝突し、原子に成った。
・1.017×10−17 m2の長さはいくらか。
1.017×10−17m2の長さ7 は、(1.017×10−17 m2)1/2=3.189×10-9m、です。
その場所は、電子のラブの集団が存在していた場所です。
電子のラブの集団の球体の大きさ=5.009×10−12mですから、その3.189×10-9m÷(5.009×10−12m)=6.367×102倍の長さです。
即ち、電子のラブの集団の球体の大きさは、6.367×102倍に拡大し8、それに、陽子のラブは衝突した。
【符号の説明】
1 陽子のラブの集団の球体の直径=5.009×10−12m
2 電子のラブの集団の球体の直径=5.009×10−12m
3 陽子のラブの集団の球体の半径=陽子のラブの集団の球体の直径÷2=5.009×10−12m÷2=2.505×10−12m
4 陽子のラブの集団の球体と電子のラブの集団の球体の間の距離=陽子のラブの集団の球体の半径×1836=2.505×10−12m×1836=4.499×10−9m
5 半径4.499×10−9mの球体の表面積=4π×(4.499×10−9m)2=2.542×10−16m2
6 半径4.499×10−9mの球体の表面積×0.04=2.542×10−16m2×0.04=1.017×10−17 m2
7 1.017×10−17m2の長さ=3.189×10-9m
8 電子のラブの集団の球体の大きさの何倍の大きさか。3.189×10-9m÷(5.009×10−12m)=6.367×102倍の長さです。
図面
【図1】
【先行技術文献】
【特許文献1】特願2005−166134
【特許文献2】特願2005−198056
【特許文献3】特願2009−218192
【特許文献4】特願2010−269415
【特許文献5】特願2011−139785
【特許文献6】特願2015−093867