![]()
「高エネルギー加速器で観察されるもの 4」 (この考えは、2015年1月19日に出願した、特願2015−007894.に記入した)
1. 陽子の中に3つの輪がある場合。核磁子を基に陽子の中の1つの輪のエネルギーを求める。
陽子の中の1つの輪は、輪は(1.2×102)2束で、1束は核磁子で5.0508×10−27Jです。
それで、陽子の中の1つの輪のエネルギー=(1.2×102)2束×5.0508×10−27J=7.273×10−23J。
陽子の中の3つの輪のエネルギーは其々、7.273×10−23Jです。
この陽子は高エネルギー加速器の中で、光速で回転していますので、3×108倍のエネルギーに成っています。
7.273×10−23J×3×108=2.182×10−14J、です。
・これは何MeVか。
1J=6.2415×1018eVですから、
2.182×10−14J×6.2415×1018eV=1.362×105eV=0.1362MeV
これは、陽子の中の1つの輪の電磁気のエネルギーを核磁子から計算した値です。
uクオークのスピンは1/2で、1.7〜3.1MeVです。
私の計算では0.1362MeVです。
これは、陽子のラブの公転軌道を核磁子から計算したからです。
しかし、陽子のラブの公転軌道は、真実はもっと小さい軌道で、高エネルギーの軌道です。
それで、1つの輪は0.1362MeVではなく、1.7〜3.1MeVであると考える。
2. 陽子の中のuクオークと見做される電磁気の輪が其々
3.1MeVと1.7MeVの場合どのようであるか。
○クオークと見做されているもの=3.1MeVである場合。
・1つの輪は0.1362MeVではなく、3.1MeVであるとすると、何倍のエネルギーであるか。
3.1MeV÷0.1362MeV=22.76倍
1つの束は、核磁子の22.76倍のエネルギーです。
それで、1束のエネルギーを22.76倍のエネルギーとする。
1束のエネルギーは、5.0508×10−27J×22.76=1.150×10−25J、です。
1束のエネルギーは1.150×10−25Jです。
1輪のエネルギーは、1.150×10−25J×(1.2×102)2束=1.656×10−21J、です。
1輪の電磁気の個数=1束の電磁気の個数×1輪の束数=4.34×104個×(1.2×102)2=6.2496×108個
検算
1.656×10−21Jは何MeVか。
1.656×10−21J×6.2415×1018eV=1.034×10−2eV
1.034×10−2eV×3×108=3.102×106eV=3.102MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束のエネルギーは、5.0508×10−27J×22.76=1.150×10−25J、です。
これは、(4.34×104)2回の自転でできたエネルギーですから、(4.34×104)2個の磁気の光子です。
1個の磁気の光子のエネルギーは、1.150×10−25J÷(4.34×104)2個=6.105×10−35 J、です。
磁気の光子1個のエネルギーは、6.105×10−35Jですから、
陽子の中で、磁気の光子の自転軌道は、2006年11月5日に提出した特願2006−336352より、
陽子の中で、1自転で作る磁気の光子1個のエネルギーは、1.121×10−53Jm÷自転軌道、ですから、
軌道=1.121×10−53Jm÷磁気の光子1個のエネルギー=1.121×10−53Jm÷(6.105×10−35J)=1.836×10−19m、です。
磁気の光子1個のエネルギーは6.105×10−35Jで、軌道は1.836×10−19mです。
・電気の光子1個のエネルギーと軌道はいくらか。
電気の光子1個のエネルギーは、磁気の光子の4.34×104個分ですから、6.105×10−35J×4.34×104個=2.650×10−30J、です。
陽子の中で、電気の光子の軌道は、2006年11月5日に提出した特願2006−336352より、
陽子の中で、電気の光子の軌道=6.724×10−45Jm÷1個の電気の光子のエネルギー、ですから、
電気の光子の軌道=6.724×10−45Jm÷(2.650×10−30J)=2.537×10−15m、です。
電気の光子1個のエネルギーは、2.650×10−30Jで、軌道は2.531×10−15mです。
陽子のラブの公転により電気の光子ができるので、陽子のラブの公転軌道=電気の光子の軌道=2.531×10−15m
・陽子のラブの公転軌道エネルギーはいくらか。
陽子のラブの公転軌道エネルギー=陽子のラブのエネルギー×陽子のラブの公転軌道=1.5×10−10J×2.531×10−15m=3.797×10−25Jm。
陽子のラブの公転軌道エネルギーは3.797×10−25Jmです。
陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は0.1362MeVではなく、3.1MeVである場合
表1
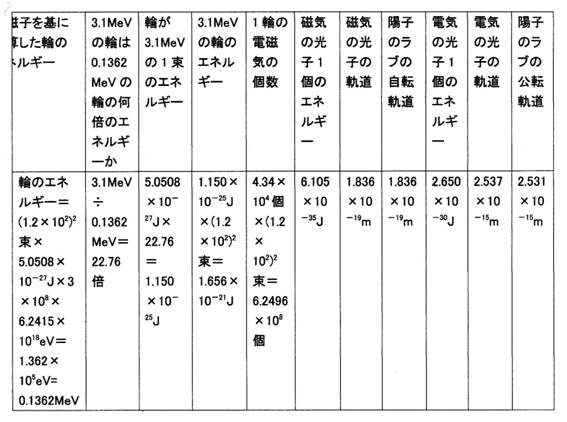
更に、この3.1MeVの電磁気の輪は軌道を大きくし、エネルギーを小さくしながら拡大し、1.7MeVの電磁気に成る。
○クオークと見做されているもの=1.7MeVである場合。
・1つの輪は0.1362MeVではなく、1.7MeVであるとすると、何倍のエネルギーであるか。
1.7MeV÷0.1362MeV=12.482倍
1つの束は、核磁子の12.482倍のエネルギーです。
それで、1束のエネルギーを12.482倍のエネルギーとする。
1束のエネルギーは、5.0508×10−27J×12.482=6.304×10−25J、です。
1束のエネルギーは6.304×10−25Jです。
1輪のエネルギーは、6.304×10−25J×(1.2×102)2束=9.078×10−22J、です。
1輪の電磁気の個数=1束の電磁気の個数×1輪の束数=4.34×104個×(1.2×102)2=6.2496×108個
検算
9.078×10−21Jは何MeVか。
9.078×10−21J×6.2415×1018eV=5.666×10−3eV
5.666×10−3eV×3×108=1.716×106eV=1.700MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束のエネルギーは、5.0508×10−27J×12.482=6.304×10−26J、です。
これは、(4.34×104)2回の自転でできたエネルギーですから、(4.34×104)2個の磁気の光子です。
1個の磁気の光子のエネルギーは、6.304×10−25J÷(4.34×104)2個=3.347×10−35J、です。
磁気の光子1個のエネルギーは、3.347×10−35Jですから、
陽子の中で、磁気の光子の自転軌道は、2006年11月5日に提出した特願2006−336352より、
陽子の中で、1自転で作る磁気の光子1個のエネルギーは、1.121×10−53Jm÷自転軌道、ですから、
軌道=1.121×10−53Jm÷磁気の光子1個のエネルギー=1.121×10−53Jm÷(3.347×10−35J)=3.349×10−19m、です。
磁気の光子1個のエネルギーは3.347×10−35Jで、軌道は3.349×10−19mです。
・電気の光子1個のエネルギーと軌道はいくらか。
電気の光子1個のエネルギーは、磁気の光子の4.34×104個分ですから、3.349×10−35J×4.34×104個=1.453×10−30J、です。
陽子の中で、電気の光子の軌道は、2006年11月5日に提出した特願2006−336352より、
陽子の中で、電気の光子の軌道=6.724×10−45Jm÷1個の電気の光子のエネルギー、ですから、
電気の光子の軌道=6.724×10−45Jm÷(1.453×10−30J)=4.628×10−15m、です。
電気の光子1個のエネルギーは1.453×10−30Jで、軌道は4.628×10−15mです。
陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は1.7MeVである場合
表2
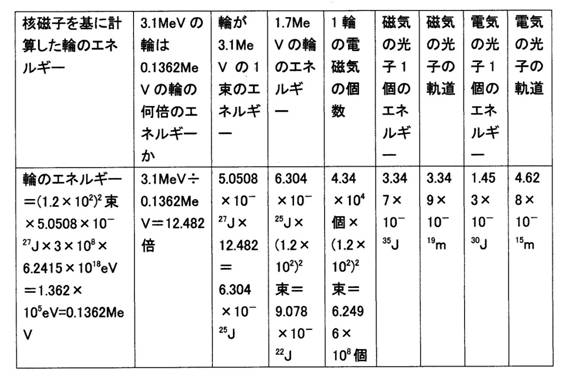
3.1MeVの電磁気の輪は軌道を大きくし、エネルギーを小さくしながら拡大し、1.7MeVの電磁気の輪に成る。
磁気の光子の軌道は3.349×10−19m となり、磁気の光子1個のエネルギーは3.347×10−35J になる。
電気の光子の軌道は4.628×10−15m となり、電気の光子1個のエネルギーは1.453×10−30J になる。
軌道は、4.628×10−15m÷(2.537×10−15m)=1.824倍になり、エネルギーは1.453×10−30J÷(2.650×10−30J)=5.483×10−1倍になった。1.824分の1になった。
輪のエネルギーは電磁気のエネルギーで1.7MeVです。
このように、陽子の中の電磁気はエネルギーを減少し、軌道を大きくする。
3. 陽子の中のクオークは、uクオークが2個、dクオークが1個であると考えられている。このクオークと見做されているものの回転方向はどのようになっているのか。
私は、陽子のラブの回転方向と電子のラブの回転方向は逆であると認識している。
それで、陽子のラブが作る電磁気の回転方向と、電子のラブが作る電磁気の回転方向は逆であり、陽子の中はuクオークだけであり、陽子の中にはdクオークは存在しないと考える。
4. 3つの輪(クオークと見做されているもの)が存在する軌道はそれぞれ異なるので、輪のエネルギーは其々異なる。3つの輪のエネルギーは同じではない。
それで、3つの輪(クオークと見做されているもの)のエネルギーは特定の値ではなく3つの軌道のエネルギーである。それはエネルギーの範囲で示される。
5. 陽子の中の1輪の電磁気がどのようであるか。
陽子の中の1個の電磁気はどのようになっているか。
それは陽子のラブが作ったものです。
陽子のラブは1公転で1本の電気の光子ができ、1公転する陽子のラブは、1公転する間に4.34×104回自転し、4.34×104個の磁気の光子を作ります。
それで、電気の光子1本の中には4.34×104個の磁気の光子が存在します。1本の電磁気は1本の電気の光子の中に4.34×104個の磁気の光子が存在する物です。
仮に、3.1MeVのように、陽子のラブの公転軌道が2.531×10−15mであるとすると、半径1.266×10−15mの球体を1公転する電気の光子1本には、直径2×π×1.266×10−15m÷(4.34×104個)=1.832×10−19mの磁気の光子が4.34×104個存在する。
それが、1本の電磁気です。1本の電磁気の半径は1.266×10−15mで、太さは1.832×10−19mです。
6. 陽子の中の1束の電磁気はどのようになっているか。
核磁子は1束のエネルギーです。この事は、陽子の中で、電磁気は束に成っている。4.34×104個の電磁気が束に成っている。
4.34×104個の電磁気は4.34×104本の線で、これが束に成っています。
束の直径には、(4.34×104個)1/2=2.083×102本の電磁気が並んでいる。
その直径=束の数×束の直径=2.083×102本×1.832×10−19m=3.816×10−17m、です。
これはドーナツ状になっている。
中空の半径は1.266×10-15mで、ドーナツの太さは3.816×10-17mです。
太さは重なり合うので、これより細い。
7. 陽子の中の輪の電磁気はどのようになっているか。
輪には、束の電磁気の本数×輪の束の数=4.34×104本×(1.2×102)2=6.250×108本の電磁気が存在する。
輪の直径には、(6.250×108本)1/2=2.5×104本の電磁気が存在する。
この太さは、電磁気1本の太さ×電磁気の数=1.832×10-19m×2.5×104本=4.58×10-15m、です。
この太さは重なり合うのでもっと細くなる。
即ち輪はドーナツ状になっている。中空の半径は1.266×10-15mで、太さは4.58×10-15m、です。
太さは磁気の光子が重なり合うのでもっと小さい。
太さは、高軌道エネルギー=高引力によって収縮されているので、中央の磁気の光子は押されて縮むのでもっと小さい。
まとめて表に示す。
陽子の中の1個の電磁気と1束の電磁気と1輪の電磁気
表3
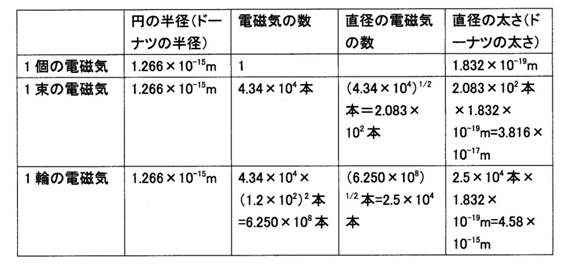
8. 陽子の中の輪は外から観察するとどのようであるか。
輪はドーナツ状になっている。中空の半径は1.266×10-15mで、太さは4.58×10-15m、です。それで、輪の半径が5.846×10-15mの球体として観察される。
この球体がクオークと見做されている。
9. 1輪の電磁気はどのように移動するか。
輪はエネルギーを減少させながら外側の軌道に移動します。
輪をクオークとした場合、陽子の中の軌道から3方向に飛ぶものである。出発点の軌道のエネルギーが輪のエネルギーと成る。
輪の束数は、3つのクオークとした場合、(1.2×102)2束です。
10. 核磁子は陽子から出る磁気の光子です。それは束に成っています。核磁子が観察されるのであるから、陽子の中は磁気の光子と電気の光子に分かれて存在しているのかもしれない。もし、陽子の中の光子は電磁気としてまとまって存在しているのではない場合、陽子の中の光子も電気の光子と磁気の光子に分かれて存在している。その場合はどのようであるか。
陽子の中の光子は電磁気ではなく、電気の光子と磁気の光子に分かれているので、輪の数は偶数です。
11. 核磁子は束に成っていているのですから、陽子の中も核磁子と同じ束になって回転しているとしたら、何個の束が存在するか。
束の数=陽子のエネルギー÷核磁子のエネルギー=1.5×10−10J÷(5.0508×10−27J)=2.970×1016(個)
磁気の光子のエネルギー=電気の光子のエネルギーですから、陽子の中の束の数は、2.970×1016個÷2=1.485×1016個です。
核磁子は束に成っていているのですから、陽子の中も核磁子と同じ束になって回転している場合、陽子の中の束の数は、1.485×1016個です。
12. 束と引力の関係はどのようになっているか。
陽子の中において、外側の軌道の核磁子の束は、4.34×104公転でできる磁気の光子が1束に成っていて、高エネルギー加速器で観察される束は3つの輪に成り、1つの輪は核磁子の束の(1.2×102)2倍に成っている。
地表の陽子の外側の軌道は、5.764×10−14mです。
・地表の陽子の外側の核磁子の軌道は加速器で観察される輪の軌道の何倍か。
1つの輪が3.1MeVの輪の軌道は、2.531×10−15mです。
地表の陽子の外側の核磁子の軌道÷3.1MeVの輪の軌道=5.764×10−14m ÷(2.531×10−15m)=2.277×10(倍)
地表の陽子の外側の核磁子の軌道は、3.1MeVの輪の軌道の2.277×10倍です。エネルギーは22.77分の1です。
・3.1MeVの輪の軌道の電気の光子1個のエネルギーは地表の陽子の外側の核磁子の軌道の電気の光子1個のエネルギーの何倍か。
2006年11月15日に提出した、特願2006−336352より、陽子のラブが1公転で作る電気の光子1個のエネルギーを求める式=6.724×10−45Jm÷軌道、の式を用いる。
地表の陽子の外側の核磁子の軌道の電気の光子1個のエネルギー=6.724×10−45Jm÷(5.764×10−14m)=1.167×10−31J
3.1MeVの輪の軌道の電気の光子1個のエネルギー=6.724×10−45Jm÷(2.531×10−15m)=2.657×10−30J
3.1MeVの輪の軌道の電気の光子1個のエネルギー÷地表の陽子の外側の核磁子の軌道の電気の光子1個のエネルギー=2.657×10−30J÷(1.167×10-31J )=2.277×10(倍)
3.1MeVの輪の軌道の電気の光子1個のエネルギーは地表の陽子の外側の核磁子の軌道の電気の光子1個のエネルギーの2.277×10倍です。
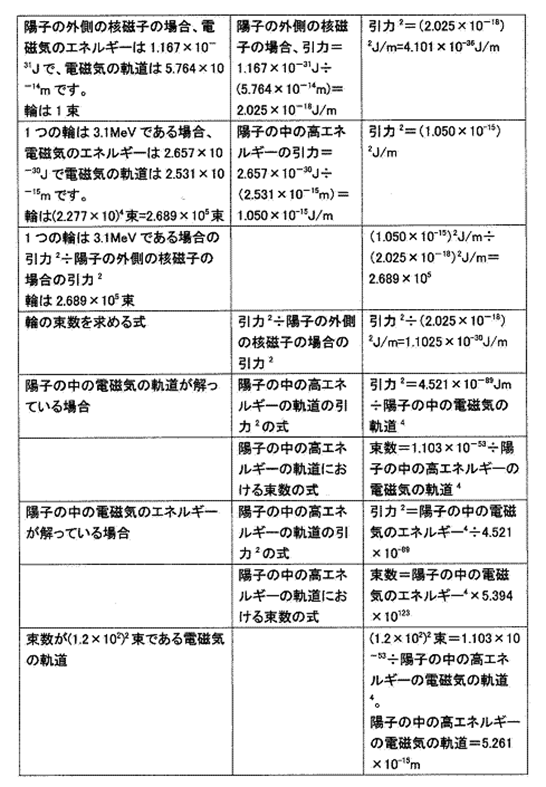
・引力2=エネルギー2÷距離2とする場合、3.1MeVの輪の軌道の引力2は地表の陽子の外側の核磁子の軌道の引力2の何倍か。
引力2=エネルギー2÷距離2とする場合、3.1MeVの輪の軌道の引力2÷地表の陽子の外側の核磁子の軌道の引力2={(2.657×10-30J)÷(2.531×10-15m)}2÷{(1.167×10-31J)÷(5.764×10-14m)}2=1.102×10-30J/m
÷(4.099×10-36J/m)=2.688×105
引力2=エネルギー2÷距離2とする場合、3.1MeVの輪の軌道の引力2は地表の陽子の外側の核磁子の軌道の引力2の2.688×105倍です。
・束の数は引力2に比例するなら、3.1MeVの輪の数は地表の陽子の外側の核磁子の束の数の何倍か。
3.1MeVの輪の軌道の引力2は地表の陽子の外側の核磁子の軌道の引力2の2.688×105倍ですから、3.1MeVの輪の束数は地表の陽子の外側の核磁子の束数の2.688×105倍です。
束の数は引力2に比例するなら、3.1MeVの輪の束の数は地表の陽子の外側の核磁子の束数の(2.277×10)4=2.688×105倍です。
・陽子の中において、外側の核磁子の軌道の束は1束に成っていて、3.1MeVの輪は3つの輪に成り、1つの輪は地表の陽子の外側の核磁子の束の(1.2×102)2倍に成っている。この事は何を物語るか。
1.この事は、輪の数は3つであることを物語る。
2.電磁気はその軌道の引力2により1つの輪になる。
3.陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は3.1MeVである場合、電磁気の軌道は2.531×10−15mであり、電磁気のエネルギーは2.657×10−30Jであり、輪は(2.277×10)4束です。
4.陽子の外側の電磁気の軌道は5.764×10−14mであり、電磁気のエネルギーは1.167×10−31Jであり、1束です。
5.陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は3.1MeVである場合、引力=電磁気のエネルギー÷電磁気の軌道=2.657×10−30J÷(2.531×10−15m)=1.050×10−15J/m
陽子の外側の核磁子の場合、引力=電磁気のエネルギー÷電磁気の軌道=1.167×10−31J÷(5.764×10−14m)=2.025×10−18J/m
6.陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は3.1MeVである場合の引力2÷陽子の外側の核磁子の場合の引力2はいくらか。
(1.050×10−15)2J/m÷(2.025×10−18)2J/m=2.689×105
陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は3.1MeVである場合の引力2÷陽子の外側の核磁子の場合の引力2=2.689×105(束)です。
よって、軌道の束数はその軌道の引力2に比例する。
この事をまとめて表に示す。
陽子の中の束と引力2の関係。地表の陽子の外側を1とする。
表4
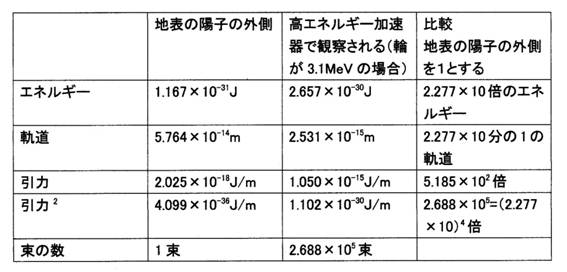
13. 束の数と軌道の引力2の関係はどのようであるか。陽子の中の電磁気の軌道が解っている場合、引力2と束の数を求める式はどのようであるか。
地表の陽子の外側の核磁子の場合、軌道の引力2は(2.025×10−18)2J/mで1束です。
陽子の中の電気の光子1個のエネルギーを求める式=6.724×10−45Jm÷陽子の中の電気の光子の軌道、の式を用いる。
・引力2=陽子の中の電磁気のエネルギー2÷陽子の中の電磁気の軌道2=(6.724×10−45Jm÷陽子の中の電磁気の軌道)2÷陽子の中の電磁気の軌道2=4.521×10−89Jm÷陽子の中の電磁気の軌道4
例えば、陽子の中の高エネルギーの電磁気の軌道=2.531×10−15mの場合。
陽子の中の高エネルギーの場合、引力2=4.521×10−89Jm÷陽子の中の電磁気の軌道4=4.521×10−89Jm÷(2.531×10−15m)4=1.102×10-30
陽子の中の電磁気の軌道が解っている場合、陽子の中の高エネルギーの引力2は、引力2=4.521×10−89Jm÷陽子の中の電磁気の軌道4、です。
・陽子の中の高エネルギーの軌道における束数=陽子の中の高エネルギーの引力2÷陽子の外側の核磁子の電磁気の光子の引力2 =4.521×10−89Jm÷陽子の中の電磁気の軌道4÷(2.025×10−18J/m )2=1.103×10−53÷陽子の中の高エネルギーの電磁気の軌道4
例えば、陽子の中の高エネルギーの電磁気の軌道=2.531×10−15mの場合。
陽子の中の高エネルギーの軌道における束数=1.103×10−53÷陽子の中の高エネルギーの電磁気の軌道4=1.103×10−53÷(2.531×10−15m)4=2.689×105(束)
陽子の中の電磁気の軌道が解っている場合、束の数を求める式は、陽子の中の高エネルギーの軌道における束数=1.103×10−53÷陽子の中の高エネルギーの電磁気の軌道4、です。
14. 束の数と軌道の引力2の関係はどのようであるか。陽子の中の電磁気のエネルギーが解っている場合、引力2と束の数を求める式はどのようであるか。
地表の陽子の外側の核磁子の場合、軌道の引力2は(2.025×10−18)2J/mで1束です。
陽子の中の電気の光子の軌道を求める式=6.724×10−45Jm÷陽子の中の電気の光子1個のエネルギー、の式を用いる。
・陽子の中の高エネルギーの場合、引力2=陽子の中の電磁気のエネルギー2÷陽子の中の電磁気の軌道2=陽子の中の電磁気のエネルギー2÷(6.724×10−45Jm÷陽子の中の電磁気のエネルギー)2=陽子の中の電磁気のエネルギー4÷(6.724×10−45Jm)2
・陽子の中の高エネルギーの軌道における束数=陽子の中の高エネルギーの電磁気の引力2÷陽子の外側の核磁子の電磁気の光子の引力2 =陽子の中の電磁気のエネルギー4÷(6.724×10−45Jm)2÷(2.025×10−18)2J/m=陽子の中の電磁気のエネルギー4×5.394×10123
電磁気のエネルギーが解っている場合、束の数を求める式は、陽子の中の高エネルギーの軌道における束数=陽子の中の電磁気のエネルギー4×5.394×10123、です。
例えば、陽子の中の高エネルギーの電磁気のエネルギーが2.657×10−30Jの場合。
・陽子の中の高エネルギーの場合、引力2=陽子の中の電磁気のエネルギー4÷(6.724×10−45Jm)2=(2.657×10−30J)4÷(6.724×10−45Jm)2=1.102×10−30J/m
・陽子の中の高エネルギーの軌道における束数=陽子の中の高エネルギーの電磁気の引力2÷陽子の外側の核磁子の電磁気の光子の引力2 =陽子の中の電磁気のエネルギー4÷(6.724×10−45Jm)2÷(2.025×10−18)2J/m=陽子の中の電磁気のエネルギー4×5.394×10123=(2.657×10−30J)4×5.394×10123=2.688×105(束)
または、陽子の中の高エネルギーの軌道における束数=陽子の中の高エネルギーの電磁気の引力2÷陽子の外側の核磁子の電磁気の光子の引力2 =1.102×10−30J/m÷(2.025×10−18)2J/m=2.687×105(束)
陽子の中の電磁気のエネルギーが解っている場合、陽子の中の高エネルギーの引力2=陽子の中の電磁気のエネルギー4÷(6.724×10−45Jm)2、です。
陽子の中の電磁気のエネルギーが解っている場合、束の数を求める式は、陽子の中の高エネルギーの軌道における束数=陽子の中の電磁気のエネルギー4×5.394×10123、です。
15. 陽子の中の高エネルギーの軌道における束数が(1.2×102)2束である電磁気の軌道はいくらか。
陽子の中の高エネルギーの軌道における束数=1.103×10−53÷高エネルギーの電磁気の軌道4=(1.2×102)2(束)
高エネルギーの電磁気の軌道4=1.103×10−53÷(1.2×102)2=7.660×10-58
電磁気の軌道=(7.660×10-58)1/4=(766×10-60)1/4=5.261×10-15(m)
陽子の中の高エネルギーの軌道における束数が(1.2×102)2束である電磁気の軌道は5.261×10-15mです。
この事を表に示す。
陽子の中の軌道の引力2と束の数の関係の式
表5
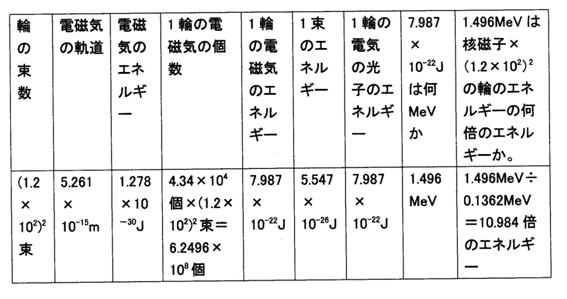
16. 陽子の中の高エネルギーの軌道における束数が(1.2×102)2束である電磁気の軌道は5.261×10-15mです。この軌道の電磁気のエネルギーはいくらか。
陽子のラブが1公転で作る電気の光子1個のエネルギーを求める式=6.724×10−45Jm÷軌道、の式を用いる。
地表の陽子の外側の軌道の電気の光子1個のエネルギー=6.724×10−45Jm÷(5.261×10−15m)=1.278×10−30J
陽子の中の高エネルギーの軌道における束数が(1.2×102)2束である軌道は5.261×10-15mで1.278×10−30Jです。
17. 輪の束数が(1.2×102)2束であり、電気の光子1個のエネルギーが1.278×10−30Jである輪の電気の光子のエネルギーはいくらか。
1輪の電磁気の個数=4.34×104個×(1.2×102)2束=6.2496×108個
1輪の電磁気のエネルギー=電気の光子1個のエネルギー×1輪の電磁気の個数=1.278×10−30J×6.2496×108個=7.987×10-22J
束数が(1.2×102)2束であり、電気の光子1個のエネルギーが1.278×10−30Jである輪の電気の光子のエネルギーは7.987×10-22Jです。
18. 1束のエネルギーはいくらか。
1輪のエネルギーは7.987×10-22Jで、これは(1.2×102)2束のエネルギーですから、1束のエネルギー=1輪のエネルギー÷束の数=7.987×10-22J÷(1.2×102)2=5.547×10-26J
1束のエネルギーは5.547×10-26Jです。
19. 1輪の電気の光子のエネルギーは7.987×10-22Jです。これは何MeVか。
7.987×10-22J×6.2415×1018eV=4.985×10-3 eV
4.985×10-3 eV×3×108=1.496×106 eV=1.496MeV
輪の電気の光子のエネルギーは7.987×10-22Jです。これは1.496MeVです。
20. 1輪の電気の光子のエネルギーは7.987×10-22Jです。これは1.496MeVです。核磁子×(1.2×102)2の輪のエネルギーの何倍のエネルギーか。
核磁子×(1.2×102)2の輪のエネルギー=5.0508×10-27J×(1.2×102)2×3×108×6.2415×1018eV=1.362×105eV=1.362×10-1MeV
1.496MeV÷0.1362MeV=10.984倍のエネルギーです。
輪の電気の光子のエネルギーは7.987×10-22Jです。これは1.496MeVです。核磁子×(1.2×102)2の輪のエネルギーの10.984倍のエネルギーです。
・1束のエネルギーはいくらか。
1束のエネルギー=5.0508×10−27J×10.984=5.548×10-26J
1束のエネルギーは5.548×10-26Jです。
この事を表に示す。
陽子の中の1輪の束数が(1.2×102)2束である場合の様子
表6
21. 軌道の引力2によりその軌道の輪の束の数は異なる。3つの輪が出発した軌道はそれぞれ異なる。この事から理解できる事は何か。
uクオークと見做されている3つの輪が出発した軌道はそれぞれ異なる。
この事によって、クオークと見做されている3つの輪のエネルギーは異なる。
それで、陽子の中のuクオークと見做される電磁気の輪のエネルギーには幅があり、1.7MeV〜 3.1MeVです。
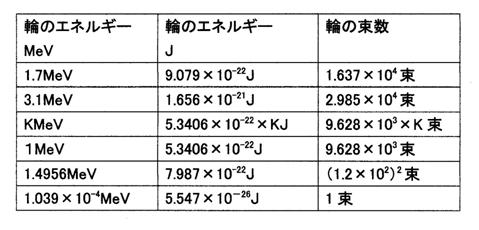
22. 輪のエネルギーが1.7MeVの場合、輪の束の数はいくらか。
・1.7MeVは何Jか。xJとする。
xJ×6.2415×1018eV×3×108=1.7×106 eV=1.7MeV
xJ=1.7×106 eV÷(6.2415×1018eV×3×108)=9.079×10-22J
輪のエネルギーは9.079×10-22Jです。
1束のエネルギーは5.547×10-26Jですから、
9.079×10-22J÷(5.547×10-26J)=1.637×104(束)です。
輪のエネルギーが1.7MeVの場合、輪の束の数は1.637×104束です。
23. 輪のエネルギーが3.1MeVの場合、輪の束の数はいくらか。
・3.1MeVは何Jか。xJとする。
xJ×6.2415×1018eV×3×108=3.1MeV=3.1×106
eV
xJ=3.1×106 eV÷(6.2415×1018eV×3×108)=1.656×10-21J
輪のエネルギーは1.656×10-21Jです。
1束のエネルギーは5.547×10-26Jですから、
1.656×10-21J÷(5.547×10-26J)=2.985×104(束)です。
輪のエネルギーが3.1MeVの場合、輪の束の数は2.985×104束です。
24. 陽子の輪のエネルギーから輪の束の数を算出する式はいくらか。陽子の輪のエネルギーはKMeVであるとする。
陽子の輪のエネルギーはKMeVであるとする。
K×106eV÷(6.2415×1018eV×3×108)=5.3406×10-22×KJ
輪の束の数=5.3406×10-22×KJ÷(5.547×10-26J)=9.628×103×K(束)
陽子の輪のエネルギーから輪の束の数を算出する式は、輪のエネルギーをKMeVとすると、輪の束の数=9.628×103×K束です。
25. 輪のエネルギーが1MeVで、輪の束の数はいくらか。
輪のエネルギーが1MeVで、輪の束の数は9.628×103束です。
26. 上記の事から、輪の束数が(1.2×102)2束である輪のエネルギーはいくらか。
9.628×103×K束=(1.2×102)2束
K=(1.2×102)2÷(9.628×103)=1.4956
輪のエネルギーが1.4956MeVである場合、輪の束数は(1.2×102)2束です。この値は19番と同じです。
27. 核磁子は1束です。この場合の束のエネルギーは5.547×10−26Jです。これは何MeVか。
5.547×10−26J×6.2415×1018eV×3×108=1.039×102eV=1.039×10-4MeV
核磁子は1束です。この場合の束のエネルギーは5.547×10−26Jで1.039×10-4MeVです。
まとめて表に示す。
陽子の輪のエネルギーから輪の束の数を算出する式。但しこのデータ-は輪の中の1束のエネルギーを5.547×10-26Jとした場合です。
表7
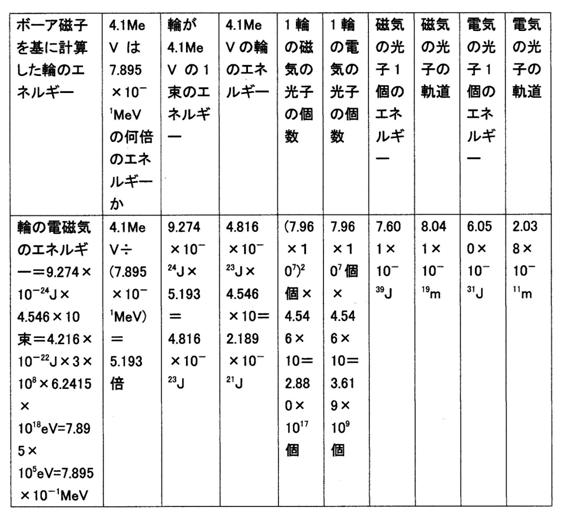
28. 電子の中のdクオークと見做される電磁気の輪が其々 4.1MeVと5.7MeVである場合どのようであるか。
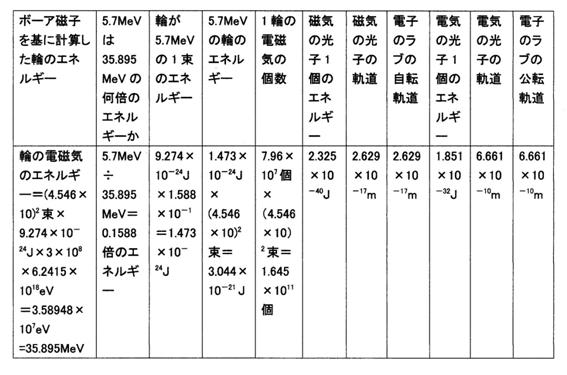
○電子の中に3つの輪がある場合。ボーア磁子を基に電子の中の1つの輪のエネルギーを求める。
電子の中の1輪の電磁気は(4.546×10)2束で、1束を9.274×10−24J(ボーア磁子)とする。
1輪の電磁気のエネルギー=(4.546×10)2束×9.274×10−24J=1.917×10−20J。1束を9.274×10−24J(ボーア磁子)としています。
電子の中の3つの輪のエネルギーは其々、1.917×10−20Jです。
このエネルギーは光速倍に成っていますので、3×108倍のエネルギーに成っています。
1.917×10−20J×3×108=5.751×10−12J、です。
・これは何MeVか。
1J=6.2415×1018eVですから、
5.751×10−12J×6.2415×1018eV=3.58948×107eV=35.895MeV
これは35.895MeVです。
1つの輪のエネルギーは35.895MeVです。
これは、1束のエネルギーを9.274×10−24J(ボーア磁子)としているからです。
真実の束のエネルギーはこれより大きく、軌道はもっと小さい。
dクオークのスピンは1/2で、4.1〜5.7MeVです。
私の計算では35.895MeVです。
これは、電子のラブの公転軌道をボーア磁子から計算したからです。
電子のラブの公転軌道は、真実はもっと小さい軌道で、高エネルギーの軌道です。
それで、1つの輪は35.895MeVではなく、4.1〜5.7MeVであると考える。
○それで、1つの輪は35.895MeVではなく、5.7MeVであるとする場合。
・1つの輪は35.895MeVではなく、5.7MeVであるとすると、何倍のエネルギーであるか。
5.7MeV÷35.895MeV=0.1588倍
1つの束は、ボーア磁子の0.1588倍のエネルギーです。
それで、1束のエネルギーを1.588×10−1倍のエネルギーとする。
1束は、ボーア磁子×1.588×10−1=9.274×10−24J×1.588×10−1=1.473×10−24J
・1輪のエネルギーは、1束のエネルギー×束数=1.473×10−24J×(4.546×10)2束=3.044×10−21 J、です。
検算
3.044×10−21J×6.2415×1018eV=1.900×10−2eV
1.900×10−2eV×3×108=5.700×106eV=5.7MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束には(7.96×107)2個の磁気の光子がありますから、
磁気の光子1個のエネルギー=1束のエネルギー÷(7.96×107)2=1.473×10−24J÷(7.96×107)2=2.325×10−40J
磁気の光子の軌道=6.112×10−57Jm÷磁気の光子1個のエネルギー=6.112×10−57Jm÷(2.325×10−40J)=2.629×10−17m
磁気の光子1個のエネルギーは2.325×10−40Jで、軌道は2.629×10−17mです。
電子のラブの自転により磁気の光子1個ができるから、電子のラブの自転軌道=磁気の光子の軌道=2.629×10−17m
電子のラブの自転軌道は2.629×10−17mです。
・電気の光子1個のエネルギーと軌道はいくらか。
1束には7.96×107公転でできた、7.96×107個の電気の光子が存在しますから、
電気の光子1個のエネルギー=1束のエネルギー÷(7.96×107個)=1.473×10−24J÷(7.96×107個)=1.851×10−32J
電気の光子の公転軌道=1.233×10−41Jm÷(1.851×10−32J)=6.661×10−10m
電気の光子1個のエネルギーは1.851×10−32Jで、軌道は6.661×10−10mです。
電子のラブの公転により電気の光子1個ができるから、電子のラブの公転軌道=電気の光子の軌道=6.661×10−10m
電子のラブの公転軌道は6.661×10−10mです。
・電子のラブの公転軌道エネルギーはいくらか。
電子のラブの公転軌道エネルギー=電子のラブの公転軌道×電子のラブのエネルギー=6.661×10−10m×8.187×10−14J=5.453×10−23Jm。
電子のラブの公転軌道エネルギーは4.186×10−23Jmです。
まとめて表に示す
電子の中に3つの輪があり、1つの輪は5.7MeVである場合。
表8
○dクオークと見做されているもの=4.1MeVである場合。
・1つの輪は35.895MeVではなく、4.1MeVであるとすると、何倍のエネルギーであるか。
4.1MeV÷35.895MeV=0.1142
1つの束は、ボーア磁子の0.1142倍のエネルギーです。
それで、1束のエネルギーを0.1142倍のエネルギーとする。
1束のエネルギーは、9.274×10−24J×0.1142=1.059×10−24J、です。
1輪のエネルギーは、1束のエネルギー×束数=1.059×10−24J×(4.546×10)2束=2.189×10−21J、です。
検算
2.189×10−21J×6.2415×1018eV=1.366×10−2eV
1.366×10−2eV×3×108=4.098×106eV=4.098MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束のエネルギーは、9.274×10−24J×0.1142=1.059×10−24J、です。
これは、(7.96×107)2回の自転でできたエネルギーですから、(7.96×107)2個の磁気の光子です。
1束には(7.96×107)2個の磁気の光子が存在しますから、
磁気の光子1個のエネルギー=1束のエネルギー÷(7.96×107)2=1.059×10−24J÷(7.96×107)2=1.671×10−40J
磁気の光子の軌道エネルギーは、6.112×10−57Jmですから、(特願2006−336352に記す) 6.112×10−57Jm÷(1.671×10−40J)=3.658×10−17m。
磁気の光子1個のエネルギーは1.671×10−40Jで、軌道は3.658×10−17mです。
・電気の光子1個のエネルギーと軌道はいくらか。
1束には7.96×107公転でできた、7.96×107個の電気の光子が存在しますから、
電気の光子1個のエネルギー=1束のエネルギー÷(7.96×107個)=1.059×10−24J÷(7.96×107個)=1.330×10−32J
この公転軌道は、1.233×10−41Jm÷(1.330×10−32J)=9.271×10−10m、です。
電気の光子1個のエネルギーは1.330×10−32Jで、軌道は9.271×10−10mです。
まとめて表に示す。
電子の中に3つの輪があり、1つの輪は4.1MeVである場合
表9
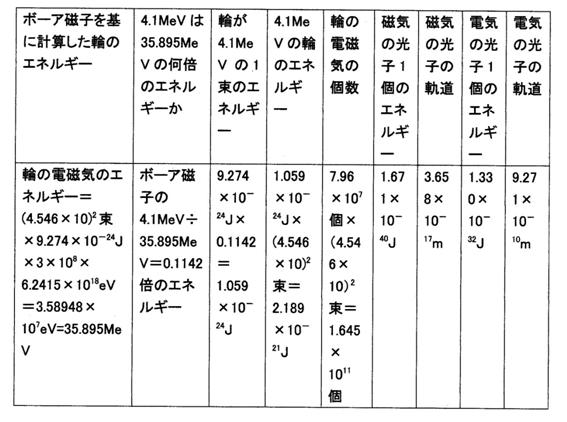
29. 電子の中で、磁気の光子と電気の光子が離れていて、輪が6つの場合はどのようであるか。輪の光子のエネルギーが5.7MeVと4.1MeVである場合。
○電子の中で輪が6つの場合。(磁気の光子と電気の光子が離れている場合) ボーア磁子を基に電子の中の1つの輪のエネルギーを求める。
電子の中はエネルギーが小さいので、磁気の光子と電気の光子が離れていると考えられる。
電子の中の電気の光子の1輪は4.546×10束で、1束を9.274×10−24J(ボーア磁子)とする。
1輪の光子のエネルギー=9.274×10−24J×4.546×10束=4.216×10−22J
電子の中の6つの輪のエネルギーは其々、4.216×10−22Jです。
このエネルギーは光速倍になっていますので、3×108倍のエネルギーに成っています。
4.216×10−22J×3×108=1.265×10−13J
1.265×10−13J×6.2415×1018eV=7.895×105eV=7.895×10−1MeV
1つの輪のエネルギーは7.895×10−1MeVです。
これは、1束のエネルギーを9.274×10−24J(ボーア磁子)としているからです。
真実の束のエネルギーはこれより大きく、軌道はもっと小さい。
dクオークのスピンは1/2で、4.1〜5.7MeVです。
私の計算では7.895×10−1MeVです。
これは、電子のラブの公転軌道をボーア磁子から計算したからです。
電子のラブの公転軌道は、真実はもっと小さい軌道で、高エネルギーの軌道です。
それで、1つの輪は7.895×10−1MeVではなく、4.1〜5.7MeVであると考える。
○輪は5.7MeVである場合。
・1つの輪は7.895×10−1MeVではなく、5.7MeVであるとすると、何倍のエネルギーであるか。
5.7MeV÷(7.895×10−1MeV)=7.220倍
1つの束は、ボーア磁子の7.220倍のエネルギーです。
それで、1束のエネルギーを7.220倍のエネルギーとする。
1束のエネルギー=9.274×10−24J×7.220=6.696×10−23J
1束のエネルギーは、6.696×10−23Jです。
1輪のエネルギーは、6.696×10−23J×4.546×10=3.044×10−21J、です。この輪が6つあります。
検算
3.044×10−21J×6.2415×1018eV=1.900×10−2eV
1.900×10−2eV×3×108=5.700×106eV=5.700MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束には(7.96×107)2個の磁気の光子がありますから、
磁気の光子1個のエネルギー=1束のエネルギー÷(7.96×107)2=6.696×10−23J÷(7.96×107)2=1.057×10−38J
磁気の光子の軌道=6.112×10−57Jm÷磁気の光子1個のエネルギー=6.112×10−57Jm÷(1.057×10−38J)=5.782×10−19m
磁気の光子1個のエネルギーは1.057×10−38Jで、軌道は5.782×10−19mです。
電子のラブの自転軌道は5.782×10−19mです。
・電気の光子1個のエネルギーと軌道はいくらか。
1束には7.96×107公転でできた7.96×107個の電気の光子が存在しますから、
電気の光子1個のエネルギー=1束のエネルギー÷(7.96×107個)=6.696×10−23J÷(7.96×107個)=8.412×10−31J
電気の光子の軌道=1.233×10−41Jm÷(8.412×10−31J)=1.466×10−11m
電気の光子1個のエネルギーは8.412×10−31Jで、軌道は1.466×10−11mです。
電気の光子は電子のラブの公転によりできた物であるから、電気の光子の軌道=電子のラブの公転軌道=1.466×10−11mです。
・電子のラブの公転軌道エネルギーはいくらか。
電子のラブの公転軌道エネルギー=電子のラブの公転軌道×電子のラブのエネルギー=1.466×10−11m×8.187×10−14J=1.200×10−24Jm
電子のラブの公転軌道エネルギーは1.200×10−24Jmです。
まとめて表に示す。
電子の中に6つの輪があり、1つの輪は5.7MeVであるとする場合。
表10
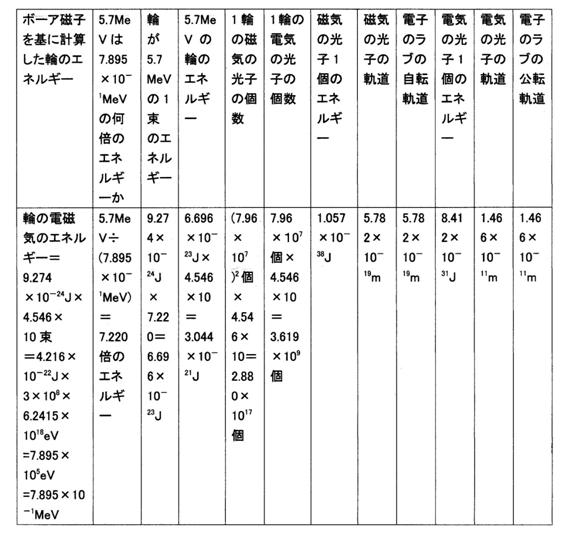
○輪は4.1MeVである場合。
・1つの輪は7.895×10−1MeVではなく、4.1MeVであるとすると、何倍のエネルギーであるか。
4.1MeV÷(7.895×10−1MeV)=5.193倍
1つの束は、ボーア磁子の5.193倍のエネルギーです。
それで、1束のエネルギーを5.193倍のエネルギーとする。
1束のエネルギー=9.274×10−24J×5.193=4.816×10−23J
1束のエネルギーは、4.816×10−23Jです。
1輪のエネルギーは、4.816×10−23J×4.546×10=2.189×10−21J、です。この輪が6つあります。
検算
2.189×10−21J×6.2415×1018eV=1.366×10−2eV
1.366×10−2eV×3×108=4.098×106eV=4.098MeV
・磁気の光子1個のエネルギーと軌道はいくらか。
1束には(7.96×107)2個の磁気の光子がありますから、
磁気の光子1個のエネルギー=1束のエネルギー÷(7.96×107)2=4.816×10−23J÷(7.96×107)2=7.601×10−39J
磁気の光子の軌道=6.112×10−57Jm÷磁気の光子1個のエネルギー=6.112×10−57Jm÷(7.601×10−39J)=8.041×10−19m
磁気の光子1個のエネルギーは7.601×10−39Jで、軌道は8.041×10−19mです。
・電気の光子1個のエネルギーと軌道はいくらか。
1束には7.96×107公転でできた7.96×107個の電気の光子が存在しますから、
電気の光子1個のエネルギー=1束のエネルギー÷(7.96×107個)=4.816×10−23J÷(7.96×107個)=6.050×10−31J
電気の光子の軌道=1.233×10−41Jm÷(6.050×10−31J)=2.038×10−11m
電気の光子1個のエネルギーは6.050×10−31Jで、軌道は2.038×10−11mです。
まとめて表に示す。
電子の中に6つの輪があり、1つの輪は4.1MeVであるとする場合。
表11
30. 電子の中は光子が3つの輪になっているか、6つの輪になっているか。
電子の中に3つの輪があり、1つの輪は5.7MeVである場合。
電子のラブの公転により電気の光子1個ができるから、電子のラブの公転軌道=電気の光子の軌道=6.661×10−10mです。
これは、電子のラブの公転軌道=ボーア半径×2=5.2918×10-11m×2=1.05836×1010m、より大きい。
dクオークは電子の中に存在するものであるから、地表の電子のラブの公転軌道より小さいはずである。
この事によって、電子の中は光子が3つの輪になっていない。
電子の中に6つの輪があり、1つの輪は5.7MeVである場合。
電気の光子は電子のラブの公転によりできた物であるから、電気の光子の軌道=電子のラブの公転軌道=1.466×10−11mです。
この軌道は、地表のボーア半径×2の値より小さいので、電子の中に存在する電子のラブの公転軌道であると理解できる。
この事から、電子の中に存在する光子は電磁気としてまとまっておらず、電気の光子と磁気の光子は離れて存在する事が理解できる。
電子の中の光子は6つの輪になっている。
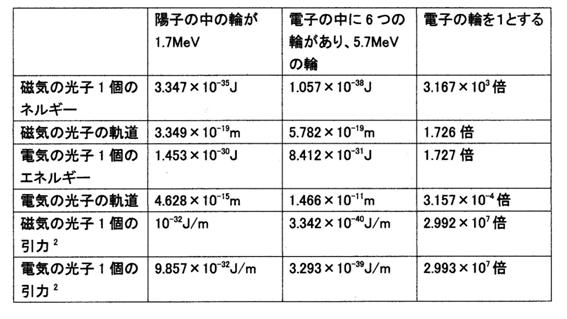
31. 電子の中で、磁気の光子と電気の光子はどのようになっているか。陽子と比較する。
・電気の光子と磁気の光子はエネルギーが弱くなると離れます。エネルギーの比較。
陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は1.7MeVである場合。
磁気の光子1個のエネルギーは3.347×10−35Jで軌道は3.349×10−19mです。
電気の光子1個のエネルギーは1.453×10−30Jで、軌道は4.628×10−15mです。
電子の中に6つの輪があり、1つの輪は5.7MeVであるとする場合。
磁気の光子の1個のエネルギーは1.057×10−38Jで、軌道は5.782×10−19mです。
電気の光子1個のエネルギーは8.412×10−31Jで、軌道は1.466×10−11mです。
陽子の中に3つの輪の磁気の光子1個のエネルギー÷電子の中に6つの輪があり、1つの輪は5.7MeVの磁気の光子1個のエネルギー=3.347×10−35J÷(1.057×10−38J)=3.167×103(倍)
陽子の中のエネルギーは電子の中のエネルギーの3.167×103倍です。
・電気の光子と磁気の光子は引力2が弱くなると離れます。引力2の比較
陽子の中に3つの輪(クオークと見做されているもの)があり、1つの輪は1.7MeVである場合。
磁気の光子1個の引力2は、(3.347×10−35J)2÷(3.349×10−19m)2=10-32J/m
電気の光子1個の引力2は、(1.453×10−30J)2÷(4.628×10−15m)2=9.857×10-32J/m
電子の中に6つの輪があり、1つの輪は5.7MeVである場合。
磁気の光子1個の引力2は、(1.057×10−38J)2÷(5.782×10−19m)2=3.342×10-40J/m
電気の光子1個の引力2は、(8.412×10−31J)2÷(1.466×10−11m)2=3.293×10-39J/m
陽子の中に3つの輪の磁気の光子1個の引力2÷電子の中に6つの輪があり、1つの輪は5.7MeVである磁気の光子1個の引力2=10-32J/m÷(3.342×10-40J/m)=2.992×107(倍)
陽子の中に3つの輪の電気の光子1個の引力2÷電子の中に6つの輪があり、1つの輪は5.7MeVである電気の光子1個の引力2=9.857×10-32J/m÷(3.293×10-39J/m)=2.993×107(倍)
よって、電子の中に6つの輪があり、1つの輪は5.7MeVである場合は引力2が弱いので電気の光子と磁気の光子は分離している。
尚、電子の中に3つの輪があり、1つの輪は5.7MeVである場合は、電子の中に6つの輪があり、1つの輪は4.1MeVである場合よりエネルギーが小さいので比較する必要はない。
まとめて表に示す。
電子の中で、磁気の光子と電気の光子はどのようになっているか。陽子の中と電子の中のエネルギーと引力2の比較
表12
32. 電子の中で、磁気の光子は束に成り存在する。どのような束になっているか。
電子の中に6つの輪があり、1つの輪は5.7MeVである場合。
磁気の光子は7.96×107個が1本の線で円になっています。その円の半径は1.466×10−11m÷2=7.33×10-12m、です。線の太さは5.782×10−19mです。
その線が束に成っています。束の線は7.96×107本ですから直径には(7.96×107本)1/2=8.922×103本存在します。
この太さは、1本の線の太さ×線の数=5.782×10−19m×8.922×103本=5.159×10-15m、です。
束の円の半径は7.33×10-12mで、円の太さは5.159×10-17mです。これはドーナツ状に成っている。
33. 1つの輪の磁気の光子はどのようであるか。
電子の中に6つの輪があり、1つの輪は5.7MeVである場合。
1つの輪には4.546×10束存在します。
輪には、7.96×107本×4.546×10束=3.619×109本
輪の直径に、(7.96×107本×4.546×10束)1/2=(3.619×109本)1/2=6.016×104本、存在します。
この太さは、1本の線の太さ×線の数=5.782×10−19m×6.016×104本=3.478×10-14m、です。
1つの輪の中空の半径は7.33×10-12mで、輪の太さは3.478×10-14mです。
ドーナツ型に成って回転しているドーナツの中空の半径は7.33×10-12mで、ドーナツの太さは3478×10-14mです。太さは重なり合うのでもっと小さくなっている。
まとめて表に示す。
電子の中の、1本の磁気の光子と1束の磁気の光子と1輪の磁気の光子
表13
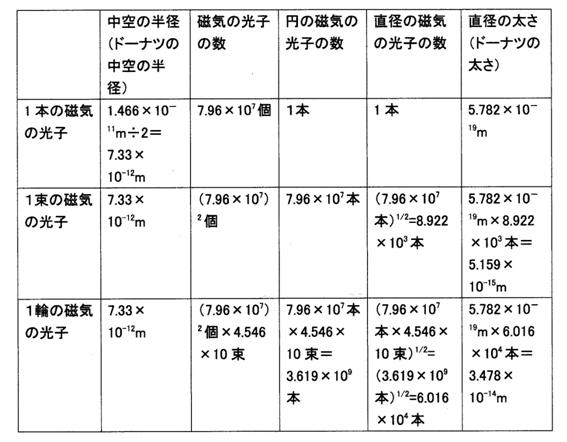
34. ボーア磁子の1本の磁気の光子の線と1束の磁気の光子はどのようであるか。
ボーア磁子は電子の外側の軌道に存在する磁気の光子の束のエネルギーです。
電子のラブが公転する直径は1.058×10-10mですから、半径は1.058×10-10m÷2=5.291×10-11m、です。
電子のラブは1公転するとき、7.96×107回自転し、7.96×107個の磁気の光子を作ります。
磁気の光子の軌道は、公転軌道×3.14÷(中空の半径は7.33×10-12mで、)=3.14×1.058×10-10m÷(7.96×107個)=4.174×10-18m、です。
電子のラブが1公転で作った磁気の光子の線を1本の磁気の光子の線とします。
1束には7.96×107公転でできる磁気の光子の線7.96×107線存在します、この磁気の光子の個数は(7.96×107)2個です。
それで、磁気の光子1個のエネルギーは、ボーア磁子÷(7.96×107)2個=9.274×10-24J÷(7.96×107)2個=1.464×10-39J、です。
束には7.96×107本の磁気の光子の線が存在します。
束の直径には、(7.96×107本)1/2=8.922×103本の磁気の光子の線が存在します。
束の直径は、磁気の光子の直径×直径の磁気の光子の線の本数=4.174×10-18m×8.922×103本=3.724×10-14m、です。
ボーア磁子の磁気の光子1個のエネルギーは1.464×10-39Jで、1本の磁気の光子の線には7.96×107個の磁気の光子が存在し、束の直径には8.922×103本の磁気の光子の線が存在します。束の直径は3.724×10-14m、です。
まとめて表に示す。
ボーア磁子の1本の磁気の光子の線と1束の磁気の光子
表14
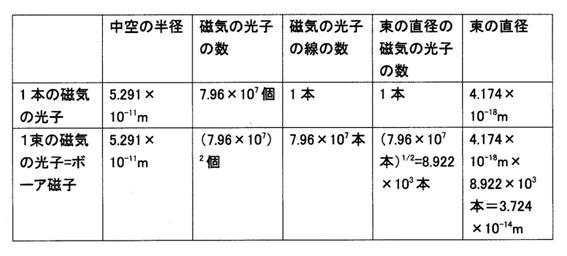
35. 電子の中の束数と引力2の関係はどのようになっているか。
1.ボーア磁子の場合。
電子の中に於いて、外側の1.058×10-10mの軌道の磁気の光子は束に成っていて1束の磁気の光子が存在する。
磁気の光子1個のエネルギーは、1.464×10-39Jで、磁気の光子の軌道は4.174×10-18mです。
2.電子の中に6つの輪があり、1つの輪は5.7MeVである場合。
磁気の光子1個のエネルギーは、1.057×10−38Jで、磁気の光子の軌道は5.782×10−19mです。
ボーア磁子の磁気の光子1個のエネルギーは1.464×10-39Jで、軌道は4.174×10-18mです。
ボーア磁子との比較
電子の外側のボーア磁子の磁気の光子1個のエネルギーは1.464×10-39Jです。
電子の中の1つの輪は5.7MeVである場合、磁気の光子1個のエネルギーは1.057×10−38Jです。
1.057×10−38J÷(1.464×10-39J)=7.220(倍)
電子の外側のボーア磁子の磁気の光子の軌道は4.174×10-18mです。
電子の中の1つの輪は5.7MeVである場合、磁気の光子の軌道は5.782×10−19mです。
4.174×10-18m÷(5.782×10−19m)=7.219(倍)
・引力2=エネルギー2÷軌道2とする場合、1つの輪は5.7MeVの軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の何倍か。
1つの輪は5.7MeVである場合の軌道の引力2=(1.057×10−38J)2÷(5.782×10−19m)2=3.342×10-40J/m
電子の外側のボーア磁子の軌道の引力2=(1.464×10-39J)2÷(4.174×10-18m)2=1.230×10-43J/m
3.342×10-40 J/m÷(1.230×10-43 J/m)=2.717×103(倍)
1つの輪は5.7MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の2.717×103倍です。これは7.224=2.710×103倍です。
3.電子の中に6つの輪があり、1つの輪は4.1MeVである場合。
磁気の光子1個のエネルギーは、7.601×10−39J で、磁気の光子の軌道は8.041×10−19mです。
ボーア磁子との比較
電子の外側のボーア磁子の磁気の光子1個のエネルギーは1.464×10-39Jです。
電子の中の1つの輪は4.1MeVである場合、磁気の光子1個のエネルギーは、7.601×10−39J です。
7.601×10−39J÷(1.464×10-39J)=5.192(倍)
電子の外側のボーア磁子の磁気の光子の軌道は4.174×10-18mです。
電子の中の1つの輪は4.1MeVである場合、磁気の光子の軌道は、8.041×10−19mです。
4.174×10-18m÷(8.041×10−19m)=5.191(倍)
・引力2=エネルギー2÷軌道2とする場合、1つの輪は4.1MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の何倍か。
1つの輪は4.1MeVである場合の軌道の引力2=(7.601×10−39J)2÷(8.041×10−19m)2=8.936×10-41J/m
電子の外側のボーア磁子の軌道の引力2=(1.464×10-39J)2÷(4.174×10-18m)2=1.230×10-43J/m
8.936×10-41J/m÷(1.230×10-43J/m)=7.265×102
1つの輪が4.1MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の7.265×102倍です。これは5.19154=7.265×102倍です。
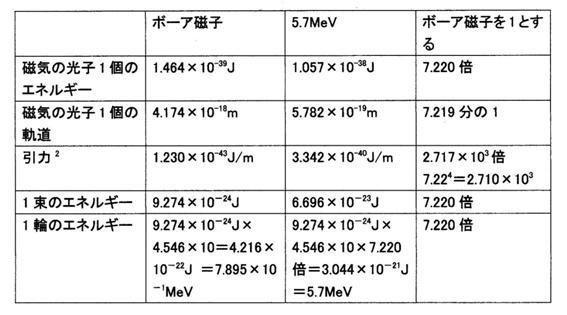
まとめて表に示す。
電子の外側のボーア磁子の軌道と、電子の中の1つの輪は5.7MeVである場合の軌道の比較
表15
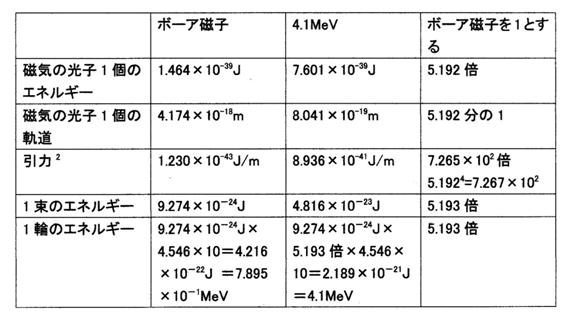
電子の外側のボーア磁子の軌道と、電子の中の1つの輪は4.1MeVである場合の軌道の比較
表16
36. 1つの輪が5.7MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の2.717×103倍です。
1つの輪が4.1MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の7.265×102倍です。これは何を示すか。
1つの輪が5.7MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の2.717×103倍です。
これは、1つの輪の束数は4.546×10ではなく(4.546×10)2=2.067×103ではないでしょうか。
その場合、電子の中に3つの輪があることになります。
1つの輪は5.7MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の2.717×103倍です。
これは、5.7MeVの輪=ボーア磁子の束の2.717×103倍の引力2です。
これは、5.7MeVの輪=ボーア磁子の束の(4.546×10)2×1.315倍の引力2です。
1つの輪は4.1MeVである場合の軌道の引力2は、電子の外側のボーア磁子の軌道の引力2の7.265×102倍です。
これは、1つの輪の束数は4.546×10ではなく(4.546×10)×1.598×10ではないでしょうか。
これは、4.1MeVの輪=ボーア磁子の束の7.265×102倍の引力2です。
これは、4.1MeVの輪=ボーア磁子の束の(4.546×10)×1.598×10倍の引力2です。
37. 陽子の中の場合、輪の束数を求める式は、輪の束数=引力2÷陽子の外側の核磁子の引力2=引力2÷(2.025×10−18)2J/m、です。電子の場合、輪の束数を求める式はどのようであるか。
・電子の外側のボーア磁子の引力2はいくらか。
電子の外側のボーア磁子の軌道は1.058×10-10mです。
この軌道の電気の光子の軌道は、1.233×10-41Jm÷(1.058×10-10m)=1.165×10-31J、です。
それで、電子の外側のボーア磁子の軌道の引力2=(1.165×10-31J)2÷(1.058×10-10m)2=1.212×10-42J/m。
電子の場合、輪の束数を求める式は、輪の束数=引力2÷電子の外側のボーア磁子の軌道の引力2=引力2÷(1.212×10-42)J/m、です。
・5.7MeVの場合の輪の束数はいくらか。
5.7MeVの場合の引力2=電気の光子のエネルギー2÷電気の光子の軌道2=(8.412×10−31J)2÷(1.466×10−11m)2=3.293×10-39J/m
輪の束数=引力2÷電子の外側のボーア磁子の軌道の引力2=3.293×10-39J/m÷(1.212×10-42J/m)=2.717×103(束)
5.7MeVの場合の輪の束数は2.717×103束です。
・4.1MeVの場合の輪の束数はいくらか。
4.1MeVの場合の引力2=電気の光子のエネルギー2÷電気の光子の軌道2=(6.050×10−31J)2÷(2.038×10−11m)2=8.813×10-40J/m
輪の束数=引力2÷電子の外側のボーア磁子の軌道の引力2=8.813×10-40J/m÷(1.212×10-42J/m)=7.271×102(束)
4.1MeVの場合の輪の束数は7.271×102束です。
38. 輪の束数がボーア磁子の束数の(4.546×10)2=2.067×103倍である場合、この軌道の引力と電気の光子のエネルギーと軌道はいくらか。
・輪の束数がボーア磁子の束数の(4.546×10)2=2.067×103倍である場合の引力はいくらか。
束数=引力2÷(1.212×10-42)J/m=2.067×103
引力2=2.067×103×(1.212×10-42)/m=2.505×10-39J/m=25.05×10-40J/m
引力=(25.05×10-40J/m)1/2=5.005×10-20J/m
輪の束数がボーア磁子の束数の(4.546×10)2=2.067×103倍である場合の引力は5.005×10-20J/mです。
・この軌道の電気の光子のエネルギーと軌道はいくらか。
この軌道の電気の光子のエネルギーをAJとする。
軌道は、1.233×10-41Jm÷AJ、です。
引力=AJ÷(1.233×10-41Jm÷AJ)=5.005×10-20J/m
A2=1.233×10-41Jm×5.005×10-20J/m=6.171×10-61J
A=(6.171×10-61J)1/2=7.856×10-31J
軌道=1.233×10-41Jm÷(7.856×10-31J)=1.570×10-11m
この軌道の電気の光子のエネルギーは7.856×10-31Jで、軌道は1.570×10-11mです。
検算
電子の場合、輪の束数を求める式は、輪の束数=引力2÷電子の外側のボーア磁子の引力2=引力2÷(1.212×10-42J/m)
軌道の電気の光子のエネルギーは7.856×10-31Jで、軌道は1.570×10-11mです。
輪の束数=引力2÷電子の外側のボーア磁子の引力2=引力2÷(1.212×10-42)J/m=(7.856×10-31J)2÷(1.570×10-11m)2÷(1.212×10-42J/m)=2.066×103(束)
・電気の光子のエネルギーはボーア磁子の電気の光子のエネルギーの何倍か。
7.856×10-31J÷(1.165×10-31J)=6.743(倍)
・輪のエネルギーはいくらか。
ボーア磁子×6.743×4.546×10束=9.274×10−24J×6.743×4.546×10束=2.843×10-21J
2.843×10-21J÷(5.3406×10-22J)=5.323MeV
まとめて表に示す。
輪の束数が(4.546×10)2=2.067×103束である場合
表17
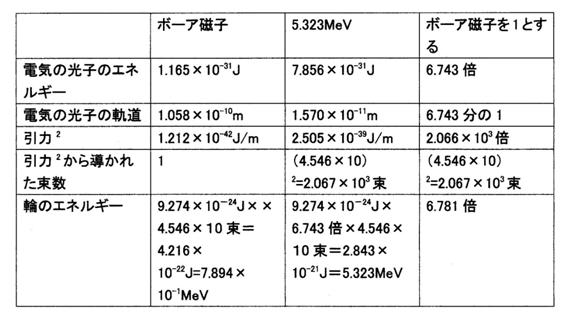
まとめて表に示す。
輪の束数=引力2÷電子の外側のボーア磁子の引力2=引力2÷(1.212×10-42)J/mの式で計算した束数と輪のエネルギー
表18
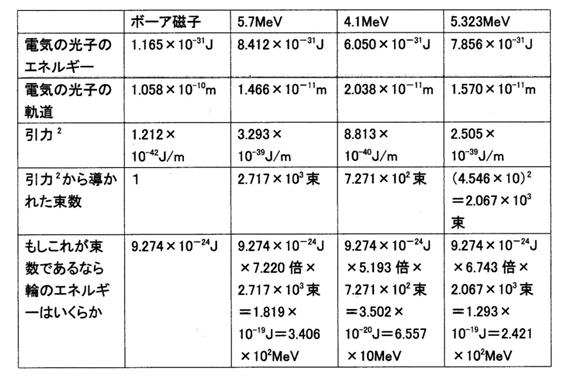
39. 引力2から導かれた数は何か。
引力2から導かれた数は1輪の束数です。
この場合、束のエネルギーを一定にしています。
・束のエネルギーはいくらか。
輪のエネルギーが5.7MeVの場合。
1MeV=5.3406×10-22J
束のエネルギー×束の数=5.7MeV=5.7×5.3406×10-22J=3.044×10-21J
束のエネルギー×2.717×103=3.044×10-21J
束のエネルギー=3.044×10-21J÷(2.717×103)=1.120×10-24J
よって、輪の1束のエネルギーが1.120×10-24Jであるとき、引力2から導かれた束数になる。
検算
輪のエネルギーが4.1MeVの場合。
束のエネルギー×束の数=1.120×10-24J×7.271×102=8.144×10-22J
8.144×10-22J÷(5.3406×10-22J)=1.525MeV
この値は4.1MeVではないので間違いです。
40. 束数と輪のエネルギーの関係はいくらか。
輪のエネルギーが5.7MeVのエネルギーは3.044×10−21 Jで、束数は2.717×103束です。
輪のエネルギーが4.1MeVのエネルギーは2.189×10−21Jで、束数は7.271×102束です。
輪のエネルギーが5.323MeV のエネルギーは2.843×10-21J で、束数は2.067×103束です。
1束のエネルギーをxJとする。
・xJ×2.717×103束=5.7×5.3406×10-22J
xJ=5.7×5.3406×10-22J÷(2.717×103束)=1.120×10-24J
・xJ×7.271×102束=4.1×5.3406×10-22J
xJ=4.1×5.3406×10-22J÷(7.271×102束)=3.011×10-24J
・xJ×2.067×103束=5.323×5.3406×10-22J
xJ=5.323×5.3406×10-22J÷(2.067×103束)=1.375×10-24J
これによって、1束のエネルギーは一定ではない。
よって、束数と輪のエネルギーの関係も一定ではない。
陽子の場合とは異なる。
陽子の場合は、1輪の束数が(1.2×102)2束の1束のエネルギーを定数としている。それは5.547×10-26Jです。
【図面の簡単な説明】
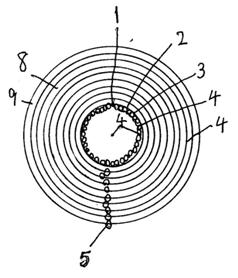
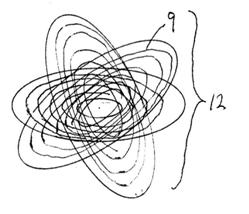
【図1】図1は陽子の中の1輪の電磁気がどのようであるかを図示する。
陽子の中の1個の電磁気はどのようになっているか。
それは陽子のラブ1が作ったものです。
陽子のラブは1公転で1本の電気の光子2ができ、1公転する陽子のラブは、1公転する間に4.34×104回自転し、4.34×104個の磁気の光子3を作ります。
それで、電気の光子1本の中には4.34×104個の磁気の光子が存在します。1本の電磁気4は1本の電気の光子の中に4.34×104個の磁気の光子が存在する物です。
仮に、3.1MeVのように、陽子のラブの公転軌道が2.531×10−15mであるとすると、半径1.266×10−15mの球体を1公転する電気の光子1本には、太さ=直径=2×π×1.266×10−15m÷(4.34×104個)=1.832×10−19mの磁気の光子が4.34×104個存在する。
それが、1本の電磁気です。1本の電磁気4の半径は1.266×10−15mで、太さは1.832×10−19mです。
陽子の中の1束の電磁気5はどのようになっているか。
核磁子は1束のエネルギーです。この事は、陽子の中で、電磁気は束に成っている。4.34×104本の電磁気が束に成っている。
4.34×104本の電磁気は4.34×104本の線で、これが束に成っています。
束の直径6には、(4.34×104個)1/2=2.083×102本の電磁気が並んでいる。
束の直径7=直径の電磁気の数×電磁気の太さ=2.083×102本×1.832×10−19m=3.816×10−17m、です。
これはドーナツ状8になっている。
半径1.266×10-15mのドーナツの太さは3.816×10-17mです。
太さは重なり合うので、これより細い。
陽子の中の輪9の電磁気はどのようになっているか。
輪には、束の電磁気の数×輪の束の数=4.34×104本×(1.2×102)2=6.250×108本の電磁気が存在する。
輪の直径10には、(6.250×108本)1/2=2.5×104本の電気の光子が存在する。
この太さは、輪の直径11=直径の電磁気の数×電磁気の太さ=2.5×104本×1.832×10-19m=4.58×10-15m、です。
この太さは重なり合うのでもっと細くなる。
即ち輪はドーナツ状になっている。半径1.266×10-15mで、太さは4.58×10-15m、です。
太さは磁気の光子が重なり合うのでもっと小さい。
太さは、高軌道エネルギー=高引力によって収縮されているので、中央の磁気の光子は押されて縮むのでもっと小さい。
陽子の中では、輪が3個回転している。
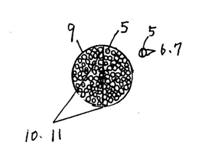
【図2】図2は輪の断面図
束の直径6には、(4.34×104個)1/2=2.083×102本の電磁気が並んでいる。
束の直径7=束の直径の電磁気の数×電磁気の直径=2.083×102本×1.832×10−19m=3.816×10−17m、です。
輪の直径10には、(6.250×108本)1/2=2.5×104本の電磁気が存在する。
輪の直径11=電磁気1本の太さ×電磁気の数=1.832×10-19m×2.5×104本=4.58×10-15m、です。
【図3】陽子の中では、輪が3個回転している。
【符号の説明】
1 陽子のラブ
2 電気の光子
3 磁気の光子。磁気の光子1個の太さ=磁気の光子1個の直径=2×π×1.266×10−15m÷(4.34×104個)=1.832×10−19m
4 1本の電磁気は1本の電気の光子の中に4.34×104個の磁気の光子が存在し、半径は1.266×10−15mで、太さは1.832×10−19m
5 束。4.34×104本の電磁気が1束に成っている。
6 束の直径には、(4.34×104個)1/2=2.083×102本の電磁気が並んでいる。
7 束の直径=直径の電磁気の数×電磁気の太さ=2.083×102本×1.832×10−19m=3.816×10−17m、です。
8 ドーナツ状
9 輪。輪には、束の電磁気の数×輪の束の数=4.34×104本×(1.2×102)2=6.250×108本の電磁気が存在する。
10 輪の直径には、(6.250×108本)1/2=2.5×104本の電磁気が存在する。
11 輪の直径=直径の電磁気の数×電磁気の太さ=2.5×104本×1.832×10-19m=4.58×10-15m、です。
12 陽子の中で、輪は3個回転している。
図面
【図1】
【図2】
【図3】
【先行技術文献】
【特許文献】
【特許文献1】特願2014−247501
【特許文献2】特願2006−336352
【特許文献3】特願2014−252526
【特許文献4】特願2014−259608