| ��N�G�[�T�[� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
10�|16���@106�N�@�����̃u���b�N�z�[���͑��z�̎��ʂ�109�{�B�N�G�[�T�[�̒������̃u���b�N�z�[�����ł����B 10�|15���@108�N�@�����̃u���b�N�z�[���͑��z�̎��ʂ�108�{�B���z�̎��ʂ�27.32�{�̐����ł����B 10�|14���@1010�N�@�����̃u���b�N�z�[���͑��z�̎��ʂ�10�V�{�B��2����̐����ł����B 10�|13���@1012�N�@�����̃u���b�N�z�[���͑��z�̎��ʂ�10�U�{�B 10�|12���@1014�N�@�����̃u���b�N�z�[���͑��z�̎��ʂ�105�{�B �Q�D�@�N�G�[�T�[�����ǂ���j�ɂ��āB(2007�N4��18���ɒ�o�����A����2007�|133476�D) 10�|16���@�@ 106�N�@�u���b�N�z�[���̏�ŃN�G�[�T�[�̒����̃u���b�N�z�[�����ł����B���z�̎��ʂ�109�{�̃u���b�N�z�[�����ł����B 5�~10�|16���@ 107�N�@�����ȉ~����̃N�G�[�T�[�ɂȂ����B 2.732�~10�|16���@ ���z�̎��ʂ�100�{�̐����ł����B 10�|15���@ 108�N�@���z�̎��ʂ�27.32�{�̐����ł����B 5�~10�|15���@ 109�N�@���z�̎��ʂ�5.464�{�̐����ł����B 3.312�~10�|15���@ ���z�̐e�ł����1����̐����ł����B 10�|14���@ 1010�N�@��2����̐����ł����B 2.732�~10�|14���@ ���z���ł����B 10�|13�� 1012�N ��͌n�̊O�����琯�����ł���B�����̐��͂܂��c���Ă���B 10�|12���@�@�@ 1014�N �@��͌n�ɑ��݂���̂̓u���b�N�z�[�������B 1.748�~10�|9���@��1020�N �|273���̏�őS�Ă��_�[�N�}�^�[�ɂȂ�B �R�D�@�N�G�[�T�[�����ǂ���j��}�ɂ���Ƃǂ̂悤�ɂȂ邩�B(2007�N4��18���ɒ�o�����A����2007�|133476�D) �N�G�[�T�[�̂��ǂ���j���A�������F���̔N��Ƃ��A�c�������]�O���Ƃ���B 10�|16���B106�N�B10�|16���̃u���b�N�z�[���̋O���̏�ŁA�N�G�[�T�[�̒������̃u���b�N�z�[�����ł���B���z�̎��ʂ�109�{�̃u���b�N�z�[�����ł���B 5�~10�|16���B107�N�B�u���b�N�z�[������W�F�b�g���˂����o���A���̓d�C�̌��q�Ǝ��C�̌��q�����͂̉��x���������A�_�[�N�}�^�[�𐅑f�ɂ���B���f���W�܂��āA�N�G�[�T�[�͍��F�̑ȉ~���ɂȂ�B �����ȉ~���̂̒����ɂ͑��z�̎��ʂ�109�{�̃u���b�N�z�[��������B 2.732�~10�|16���B���z�̎��ʂ�100�{�̐����ł����B 10�|15���B108�N�B���z�̎��ʂ�27.32�{�̐����ł����B��1����̐����ł���B 5�~10�|15���B109�N�B���z�̎��ʂ�5.464�{�̐����ł����B 10�|14���B1010�N�B��2����̐����ł���B 10�|13���B1012�N�B1010�N���10�|15����������́A10�|14���̏�ɂȂ�A�������݂���B 10�|12���B1014�N�B��͂ɑ��݂���̂̓u���b�N�z�[�������B�N�G�[�T�[�̒������ɂ��������z�̎��ʂ�109�{�̎��ʂ̃u���b�N�z�[���́A���z�̎��ʂ�105�{�̎��ʂɐ���A��͂̒������ɑ��݂���B �y�}�ʂ̊ȒP�Ȑ����z �y�}�S�z�N�G�[�T�[�����ǂ���j��}�ɂ���Ƃǂ̂悤�ɂȂ邩�B �N�G�[�T�[�̂��ǂ���j���A�������F���̔N��Ƃ��A�c�������]�O���Ƃ���B 10�|16���B106�N�B10�|16���̃u���b�N�z�[���̋O���̏�ŁA�N�G�[�T�[�̒����̃u���b�N�z�[�����ł���B 5�~10�|16���B107�N�B�u���b�N�z�[������W�F�b�g���˂����o���A���̓d�C�̌��q�Ǝ��C�̌��q�����͂̉��x���������A�_�[�N�}�^�[�𐅑f�ɂ���B���f���W�܂��āA�N�G�[�T�[�͍��F�̑ȉ~���ɂȂ�B �����ȉ~���̂̒����ɂ͑��z�̎��ʂ�109�{�̃u���b�N�z�[��������B 2.732�~10�|16���B���z�̎��ʂ�100�{�̐����ł����B 10�|15���B108�N�B���z�̎��ʂ�27.32�{�̐����ł����B��1����̐����ł���B 5�~10�|15���B109�N�B���z�̎��ʂ�5.464�{�̐����ł����B 10�|14���B1010�N�B��2����̐����ł���B 10�|13���B1012�N�B1010�N���10�|15����������́A10�|14���̏�ɂȂ�A�������݂���B 10�|12���B1014�N�B��͂ɑ��݂���̂̓u���b�N�z�[�������B��͂̒������ɂ͑��z�̎��ʂ�105�{�̃u���b�N�z�[�������݂���B �y�����̐����z �P�Q�@10�|16���B106�N�B�N�G�[�T�[�̒������̃u���b�N�z�[�����ł���B �P�R�@5�~10�|16���B107�N�B�N�G�[�T�[�͍��F�̑ȉ~���ɂȂ�B �P�S�@2.732�~10�|16���B���z�̎��ʂ�100�{�̐����ł����B �P�T�@10�|15���B108�N�B���z�̎��ʂ�27.32�{�̐����ł����B��1����̐����ł���B �P�U�@5�~10�|15���B109�N�B���z�̎��ʂ�5.464�{�̐����ł����B �P�V�@10�|14���B1010�N�B��2����̐����ł���B �P�W�@10�|13���B1012�N�B1010�N���10�|15����������́A10�|14���̏�ɂȂ�A�������݂���B �P�X�@10�|12���B1014�N�B��͂ɑ��݂���̂̓u���b�N�z�[�������B��͂̒������ɂ͑��z�̎��ʂ�105�{�̃u���b�N�z�[�������݂���B �y�}4�z 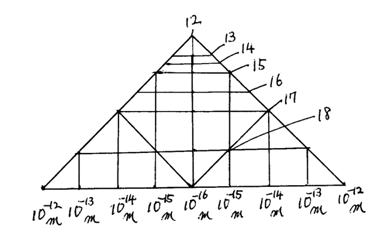 �S�D�@�N�G�[�T�[�Ƃ͉����B(2007�N8��25���ɒ�o�����A����2007�|246139�D) �F���̏����ɑ��݂������ŁA�����̃u���b�N�z�[�����W�F�b�g�o���A�_�[�N�}�^�[�i���]���Ă���d�q�̃��u�Ǝ��]���Ă���z�q�̃��u�j�␅�f���W�߁A�����̎��ʂ�傫�����Ă�����̂ł��B �T�D�@�u���b�N�z�[���̏�ŃN�G�[�T�[���ł����ꍇ�A1��3�ɂǂꂾ���̌��q�������������B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j �E���z�̎��ʂ�109�{�̃N�G�[�T�[���ł����ꍇ�A1��3�ɂǂꂾ���̌��q�������������B �u���b�N�z�[���̃W�F�b�g�łł��鋅�̂̑̐ρ�5.977�~1042��3�ł��B �W�܂������q����1.2�~1057�~109��1.2�~1066�ł��B 1��3�̌��q����1.2�~1066���i5.977�~1042��3�j��2.008�~1023�ł��B �E���z�̎��ʂ�108�{�̃N�G�[�T�[���ł����ꍇ�A1��3�ɂǂꂾ���̌��q�������������B �u���b�N�z�[���̃W�F�b�g�łł��鋅�̂̑̐ρ�5.977�~1042��3�ł��B �W�܂������q����1.2�~1057�~108��1.2�~1065�ł��B 1��3�̌��q����1.2�~1065���i5.977�~1042��3�j��2.008�~1022�ł��B �E���z�̎��ʂ�107�{�̃N�G�[�T�[���ł����ꍇ�A1��3�ɂǂꂾ���̌��q�������������B �u���b�N�z�[���̃W�F�b�g�łł��鋅�̂̑̐ρ�5.977�~1042��3�ł��B �W�܂������q����1.2�~1057�~107��1.2�~1064�ł��B 1��3�̌��q����1.2�~1064���i5.977�~1042��3�j��2.008�~1021�ł��B �E���z�̎��ʂ�106�{�̃N�G�[�T�[���ł����ꍇ�A1��3�ɂǂꂾ���̌��q�������������B �u���b�N�z�[���̃W�F�b�g�łł��鋅�̂̑̐ρ�5.977�~1042��3�ł��B �W�܂������q����1.2�~1057�~106��1.2�~1063�ł��B 1��3�̌��q����1.2�~1063���i5.977�~1042��3�j��2.008�~1020�ł��B �u���b�N�z�[���̏�łł����N�G�[�T�[�̎��ʂ�1��3�̌��q��
�u���b�N�z�[���̏�ɂ����āA 1��3�̌��q����2�~1023�̋O���ł́A���z�̎��ʂ�109�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1022�̋O���ł́A���z�̎��ʂ�108�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1021�̋O���ł́A���z�̎��ʂ�10�V�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1020�̋O���ł́A���z�̎��ʂ�106�{�̃N�G�[�T�[���ł����B �U�D�@�u���b�N�z�[���̑f�q�̎��ぁ�d�q�̃��u�̌��]�O����10�|16���̎���̉F���B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j �d�q�̃��u�̌��]�O����10�|16���̎���̉F���ɂ����āA 1��3�̌��q����2�~1023�̋O���ɂ����āA���z�̎��ʂ�109�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1022�̋O���ɂ����āA���z�̎��ʂ�108�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1021�̋O���ɂ����āA���z�̎��ʂ�10�V�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1020�̋O���ɂ����āA���z�̎��ʂ�106�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1016�̋O���ɂ����āA���z�̎��ʂ�100�{�̐����ł����B 1��3�̌��q����2�~1015�̋O���ɂ����āA���z�̎��ʂ�10�{�̐����ł����B 1��3�̌��q����2�~1014�̋O���ɂ����āA���z�̎��ʂ̐����ł����B �u���b�N�z�[���̏�ɂ����Ăł������́A�W�܂�A�ȉ~��͂�������B 10�|16���̎���A�F���́A�O��������Ă����B���̋O���́A���q���̖��x�ŕ\���ł���B �F���̒����قnj��q�̖��x�͑傫���Ȃ�B�������痣���قnj��q�̖��x�͏������Ȃ�B ���q�̖��x��1��3�̌��q���ŕ\������B 10�|16���̎���A�F���̒����́A1��3�̌��q����2�~1023�̋O���ł������B���̋O���ŁA���z�̎��ʂ�109�{�̃N�G�[�T�[���ł����B �������痣���ɏ]���āA���q�̖��x�͏������Ȃ�A2�~1022�̋O����2�~1021�̋O����2�~1020�̋O����2�~1019�̋O����2�~1018�̋O����2�~1017�̋O����2�~1016�̋O����2�~1015�̋O����2�~1014�̋O����2�~1013�̋O����2�~1012�̋O���ƂȂ��Ă���B �y�}�ʂ̊ȒP�Ȑ����z �y�}1�z�u���b�N�z�[���̑f�q�̎��ぁ�d�q�̃��u�̌��]�O����10�|16���̎���̉F���B �d�q�̃��u�̌��]�O����10�|16���̎���̉F���ɂ����āA 1��3�̌��q����2�~1023�̋O���ɂ����āA���z�̎��ʂ�109�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1022�̋O���ɂ����āA���z�̎��ʂ�108�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1021�̋O���ɂ����āA���z�̎��ʂ�10�V�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1020�̋O���ɂ����āA���z�̎��ʂ�106�{�̃N�G�[�T�[���ł����B 1��3�̌��q����2�~1016�̋O���ɂ����āA���z�̎��ʂ�100�{�̐����ł����B 1��3�̌��q����2�~1015�̋O���ɂ����āA���z�̎��ʂ�10�{�̐����ł����B 1��3�̌��q����2�~1014�̋O���ɂ����āA���z�̎��ʂ̐����ł����B �u���b�N�z�[���̏�ɂ����Ăł������́A�W�܂�A�ȉ~��͂�������B 10�|16���̎���A�F���́A�O��������Ă����B���̋O���́A���q���̖��x�ŕ\���ł���B �F���̒����قnj��q�̖��x�͑傫���Ȃ�B�������痣���قnj��q�̖��x�͏������Ȃ�B ���q�̖��x��1��3�̌��q���ŕ\������B �y�}2�z���オ�ς��ƃG�l���M�[�͕ς��B10�|16���̎��ォ��10�|15���̎���ɂȂ�ƁA�G�l���M�[��1/10�ɂȂ�B 10�|16���̎���A���S�������z�̎��ʂ�109�{�̃N�G�[�T�[�́A10�|15���̎���ɂȂ�ƁA���S�������z�̎��ʂ�108�{�̃N�G�[�T�[�ɂȂ�B 10�|16������̌��q���x��1023��/m3�̋O���́A10�|15������̌��q���x��1022��/m3�̋O���ɂȂ�B 10�|16���̎���A���S�������z�̎��ʂ�108�{�̃N�G�[�T�[�́A10�|15���̎���ɂȂ�ƁA���S�������z�̎��ʂ�10�V�{�̃N�G�[�T�[�ɂȂ�B 10�|16������̌��q���x��1022��/m3�̋O���́A10�|15������̌��q���x��1021��/m3�̋O���ɂȂ�B �y�����̐����z �P�@�g���u���b�N�z�[���́h �Q�@4�~10�|17���̎��� �R�@10�|16���̎��� �S�@1��3�̌��q����2�~1023�̋O�� �T�@1��3�̌��q����2�~1022�̋O�� �U�@1��3�̌��q����2�~1021�̋O�� �V�@1��3�̌��q����2�~1016�̋O�� �W�@1��3�̌��q����2�~1015�̋O�� �X�@1��3�̌��q����2�~1014�̋O�� �P�O�@���z�̎��ʂ�109�{�̃N�G�[�T�[ �P�P�@���z�̎��ʂ�108�{�̃N�G�[�T�[ �P�Q�@���z�̎��ʂ�10�V�{�̃N�G�[�T�[ �P�R�@���z�̎��ʂ�100�{�̐� �P�S�@���z�̎��ʂ�10�{�̐� �P�T�@���z�̎��ʂ̐� �P�U�@10�|16������ɂł��������W�܂�A�ȉ~��͂ɂȂ�B �P�V�@10�|16������ �P�W�@10�|15������ �P�X�@10�|14������ �Q�O�@���S�������z�̎��ʂ�109�{�̃N�G�[�T�[ �Q�P�@���S�������z�̎��ʂ�108�{�̃N�G�[�T�[�E��� �Q�Q�@���S�������z�̎��ʂ�107�{�̃N�G�[�T�[�E��� �Q�R�@���S�������z�̎��ʂ�106�{�̃N�G�[�T�[�E��� �Q�S�@���S�������z�̎��ʂ�105�{�̃N�G�[�T�[�E��� �Q�T�@10�|16������̌��q���x��1023��/m3�̋O�� �Q�U�@10�|16������̌��q���x��1022��/m3�̋O�� �Q�V�@10�|16������̌��q���x��1021��/m3�̋O�� �Q�W�@10�|15������̌��q���x��1022��/m3�̋O�� �Q�X�@10�|15������̌��q���x��1021��/m3�̋O�� �R�O�@10�|15������̌��q���x��1020��/m3�̋O�� �R�P�@10�|14������̌��q���x��1021��/m3�̋O�� �R�Q�@10�|14������̌��q���x��1020��/m3�̋O�� �R�R�@10�|14������̌��q���x��1019��/m3�̋O�� �y�}1�z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�y�}2�z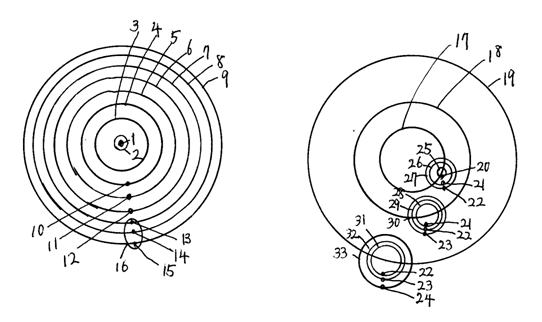 �V�D�@�F���̔N��ɂ�����A�d�q�̌��]�O���A�������������A1��3�̍ō����q���A�N�G�[�T�[���͂̒��S���̍ō����ʁB�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j 10�|16���̎����108�A10�|15���̎����109�A10�|14���̎����1010�A�ƍl����B
�W�D�@�F���̎���ɂ����āA�ǂ̋�Ԃł�1��3�̌��q���͈��ł���B�F���̎���ɂ�����1��3�̌��q���͂����炩�B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j 10�|16���̎���̉F���́A�ǂ̋�Ԃł�1��3�Ɍ��q��1018���݂����B1��3�̌��q����1018�������B 10�|15���̎���̉F���́A�ǂ̋�Ԃł�1��3�Ɍ��q��1015���݂����B1��3�̌��q����1015�������B 10�|14���̎���̉F���́A�ǂ̋�Ԃł�1��3�Ɍ��q��1012���݂����B1��3�̌��q����1012�������B 1��3�̌��q���ɂ��āB ���������������A�u���b�N�z�[���̏�łł����Ƃ���ƁA���z�̎��ʂ�100�{�̐��́A1��3�Ɍ��q����2�~1016���݂����łł��A���z�̎��ʂ�10�{�̐��́A1��3�Ɍ��q����2�~1015���݂����łł��A���z�Ɠ������́A1��3�Ɍ��q����2�~1014���݂����łł���A�Ɨ��������B ����ŁA����10�|15���̎���ɂł��܂�����A10�|15���̎���ɂ����āA1��3�̌��q����1015�ł���Ƃ��܂��B ��������ƁA10�|16���̎���́A1��3�̌��q����1018�ł��B 10�|14���̎���́A1��3�̌��q����1012�ł��B ���̎�����ɁA�N�G�[�T�[��́A�ǂꂾ���̑̐ς̌��q���W�߂Ăł������v�Z���܂��B �X�D�@���z�̎��ʂ̃��{�̃N�G�[�T�[���ł��邽�߂ɂ́A�ǂ�ʂ̑̐ς̌��q���W�߂���悢���B����͔��a���j�����B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j �N�G�[�T�[��10�|16���̎���ɂł����B 10�|16���̎���A�F���͂ǂ̏�ł��A1��3��1018�̌��q�����݂��Ă����Ƃ��܂��B ���̌��q�������z�̌��q���~����1.2�~1057�~�� �̐ς�����3�Ƃ��܂��B 1018�~����3��1.2�~1057�~�� ����3��1.2�~1057�~����1018��1.2�~1039�~�� �̐ς́A1.2�~1039�~����3�ł��B 4��3�~��3��1.2�~1039�~����3 ��3��1.2�~1039�~����3��4�~3��2.866�~1038�~����3 �����i2.866�~1038�~����3�j1/3 ����6.6�~1012�~��1/3����6.6�~109�~��1/3�j�� ���a�́A6.6�~109�~��1/3�j���ł��B �E���z�̎��ʂ�109�{�̃N�G�[�T�[���ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~109��3��1.2�~1048��3�ł��B ���a�́A6.6�~109�~109��3�j����6.6�~1012�j���ł��B �E���S�������z�̎��ʂ�108�{�̃N�G�[�T�[���ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~108��3��1.2�~1047��3�ł��B ���a�́A6.6�~109�~108��3�j����6.6�~109�~102�~1001/3=6.6�~1011�~4.643=3.064�~1012�j���ł��B �E���S�������z�̎��ʂ�107�{�̃N�G�[�T�[���ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~107��3��1.2�~1046��3�ł��B ���a�́A6.6�~109�~107��3�j����6.6�~109�~102�~101/3�j����6.6�~1011�~2.155K��=1.422�~1012Km�ł��B �E���z�̎��ʂ�100�{�̐����ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~102��3��1.2�~1041��3�ł��B ���a�́A6.6�~109�~1001/3�j����6.6�~109�~4.643�j����3.064�~1010K���ł��B �E���z�̎��ʂ�10�{�̐����ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~10��3��1.2�~1040��3�ł��B ���a�́A6.6�~109�~101/3�j����6.6�~109�~2.155�j����1.422�~1010K���ł��B �E���z�Ɠ��������ł��鎞�A���q�͂ǂ�ʂ̑̐ς���W�߂��邩�B���̔��a�͉��j�����B �̐ς́A1.2�~1039�~1��3��1.2�~1039��3�ł��B ���a�́A6.6�~109�~11/3�j����6.6�~109�j���ł��B 10�|16���̎���A�ǂ��ł�1��3��1018�̌��q�����݂��Ă���ꍇ�A���q���W�߂�ꂽ�̐ςƔ��a�B
�P�O�D�@�N�G�[�T�[�̂`�͂ǂ̂悤�ɋ��߂���̂��B 10�|16���̎���A�F���͂ǂ̏�ł��A1��3��1018�̌��q�����݂��Ă����Ƃ��܂��B ���S�������z�̎��ʂ�109�{�̃N�G�[�T�[�́A���a6.6�~1012�j���̌��q���W�߂Ăł����B �����A���ꂪ�W�F�b�g�ŏW�߂�ꂽ�Ƃ����Ȃ�A�W�F�b�g�͔��a6.6�~1012�j���܂œ͂������ɐ���܂��B �N�G�[�T�[�̂`�͂ǂ�ʂ��B �W�F�b�g�̓͂�������6.96�~105�j���~849�~�N�G�[�T�[�̂`���i3.872�~103�j��6.6�~1012�j�� �N�G�[�T�[�̂`��6.6�~1012�j�����i6.96�~105�j���~849�j�~3.872�~103��4.325�~107 ���z�̎��ʂ�109�{�̃N�G�[�T�[�̂`�́A4.325�~107�ł��B ���̒l�́A�`�����z�̒��S�̂`�~�N�G�[�T�[�̑��z�̎��ʂ̔{����3.872�~103�~109��3.872�~1012�ł͂���܂���B ����ł́A�N�G�[�T�[�̏ꍇ�́A�ǂ̂悤�Ȏ��ł`�����߂���̂ł��傤���B �N�G�[�T�[�̃W�F�b�g���͂��͈͂̌��q���W�߂�ꂽ�B �N�G�[�T�[�̃W�F�b�g���͂�����������6.6�~109�~��1/3�j���ł�����A 6.96�~105�j���~849�~�N�G�[�T�[�̂`���i3.872�~103�j��6.6�~109�~��1/3�j�� �N�G�[�T�[�̂`��6.6�~109�~��1/3�j�����i6.96�~105�j���~849�j�~3.872�~103��4.325�~104�~��1/3 ���S�������z�̎��ʂ̃��{�̃N�G�[�T�[���͂̂`�̒l�́A �`��4.325�~104�~��1/3�ł��B ����́A���z�̒��S�̉��{���B 4.325�~104�~��1/3���i3.872�~103�j��11.17�~��1/3 11.17�~��1/3�{�ł��B ����ŁA���z�̒��S�̂`��p���āA���S�������z�̎��ʂ̃��{�̃N�G�[�T�[���͂̒��S�̂`�����߂鎮�́A �N�G�[�T�[�̂`�����z�̒��S�̂`�~11.17�~��1/3�@�ł��B ����ŁA���S�������z�̎��ʂ̃��{�̃N�G�[�T�[���͂̒��S�̂`�́A���z�̎��ʂ�11.17�~��1/3�{�̐��̂`�Ɠ����l�ɐ���܂��B ���S�������z�̎��ʂ�109�{�̃N�G�[�T�[�̂`�́A���z�̎��ʂ́A109��3�~11.17��1.117�~104�{�̐��̂`�Ɠ����l�ɐ���܂��B ���S���͑��z�̎��ʂ�108�{�̃N�G�[�T�[�̂`�́A���z�̎��ʂ́A108��3�~11.17��1001/3�~102�~11.17��4.643�~102�~11.17��5.186�~103�{�̐��̂`�Ɠ����l�ɐ���܂��B �P�P�D�@�N�G�[�T�[���͂̒��S�̂`����1/3�~11.17�~���z�̒��S�̂`�@�̎��͉����Ӗ�����̂��B �N�G�[�T�[���͂̒��S�̓d�q�̃��u�̌��]�O����1.058�~10�|10�����`��1.058�~10�|10�������z�̒��S�̂`��11.17����1/3��1.058�~10�|10�����i���z�̒��S�̂`�~11.17�j����1/3 ���̎��́A�N�G�[�T�[���͂̒��S�̓d�q�̃��u�̌��]�O���́A���z�̎��ʂ�11.17�{�̐��̒��S�̓d�q�̃��u�̌��]�O���̃�1/3����1�ł��B �N�G�[�T�[���͂̒��S�̂`����1/3�~11.17�~���z�̒��S�̂`����1/3�~�i���z�̒��S�̂`�~11.17�j ���̎��́A�N�G�[�T�[���͂̒��S�̂`�́A���z�̎��ʂ�11.17�{�̐��̒��S�̂`�̃�1/3�{�ł��B �P�Q�D�@�d�q�̃��u�̃G�l���M�[�ƃW�F�b�g�̓͂������̊W�͂ǂ̂悤�ɂȂ��Ă��邩�B �W�F�b�g�̓͂�������6.96�~105�j���~849�~�`���i3.872�~103�j��1.526�~105�j���~�` �d�q�̃��u�̌��]�O����1.058�~10�|10�����` �d�q�̃��u�̃G�l���M�[��8.665�~10�|24�i�����i1.058�~10�|10�����`�j��8.190�~10�|14�i�~�` �d�q�̃��u�̃G�l���M�[��8.190�~10�|14�i�~�`�̎��B�W�F�b�g���͂�������1.526�~105�j���~�`�ł��B �d�q�̃��u�̃G�l���M�[���A�P�i�̂Ƃ��A8.190�~10�|14�i�~�`���P�i �`���P�i���i8.190�~10�|14�i�j��1.221�~1013 �W�F�b�g���͂������́A1.526�~105�j���~�`��1.526�~105�j���~1.221�~1013��1.863�~1018�j���ł��B �N�G�[�T�[�̒��������n���̎��ʂ�107�{�̎��A�d�q�̃��u�̃G�l���M�[�́A7.634�~10�|7�i�ł�����A�i���̎��͌�q����j�W�F�b�g���͂������́A1.863�~1018�j���~7.634�~10�|7�i��1.422�~1012�j���ł��B ����āA�d�q�̃��u�̃G�l���M�[�ƃW�F�b�g�̓͂������̊W�́A �W�F�b�g���͂��������d�q�̃��u�̃G�l���M�[�~1.863�~1018�j���ł��B �P�R�D�@�N�G�[�T�[�̐����B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j �N�G�[�T�[�́A���߁A�u���b�N�z�[���̑f�q���W�܂��āA�W�F�b�g���˂����B���̃W�F�b�g���˂ɂ��A���a1.126�~1011�j���܂ł̋��̂̌��q���W�܂��Ă����B �W�F�b�g���͂������́A1.526�~105�j���~�u���b�N�z�[���̂`��1.526�~105�j���~7.378�~105��1.126�~1011�j���ł��B ���̏��10�|16���̎���ŁA1��3�̌��q���͂ǂ��ł��A1018�ł���Ƃ���B���a1.126�~1011�j���܂ł̋��̂̌��q���W�܂�ƁA���z�̉��{�̎��ʂ̃N�G�[�T�[���ł��邩�B ���a1.126�~1011�j���܂ł̋��̂̌��q�������z�̌��q����4�~��3�~�i1.126�~1011�{3���j3�~1018���i1.2�~1057�j��5.977�~103 ���z�̎��ʂ�5.977�~103�{�̃N�G�[�T�[���ł���B ���z�̎��ʂ�5.977�~103�{�̃N�G�[�T�[���ł���ƁA���S���̓d�q�͌��]�O�����������Ȃ�A�G�l���M�[�͑傫���Ȃ�B����ŁA�W�F�b�g���͂��������傫���Ȃ�B�W�F�b�g���͂��������傫���Ȃ�ƁA���̋��̂���X�Ɍ��q���W�߂��A�N�G�[�T�[�̌��q���͑�������B���S���̌��q������������B ���̂悤�ɂ��āA�N�G�[�T�[�̒��S���̌��q���́A���z�̎��ʂ�104�{�����z�̎��ʂ�105�{�����z�̎��ʂ�106�{�����z�̎��ʂ�107�{�����z�̎��ʂ�108�{�����z�̎��ʂ�109�{�Ƒ�������B �P�S�D�@�N�G�[�T�[�̎��ʂƁA�`�ƁA�d�q�̃��u�̌��]�O���ƁA�d�q�̃��u�̃G�l���M�[�ƁA�W�F�b�g���͂������ƁA1��3�̌��q���ƁA���x�͂ǂ̂悤�ł��邩�B�i2007�N8��25���ɒ�o�����A����2007�|246139�D�j ���̎��ɂ���āA���߂�B���ʂ����z�̃��{�̎��B �`��4.325�~104�~��1/3 ���S���̓d�q�̃��u�̌��]�O����1.058�~10�|10�������S���̂` ���S���̓d�q�̃��u�̃G�l���M�[��8.665�~10�|24�i�������S���̓d�q�̃��u�̌��]�O�� �W�F�b�g���͂��������d�q�̃��u�̃G�l���M�[�~1.863�~1018�j��=6.6�~109Km�~��1/3 ���S����1��3�̌��q�����i10�|16�����d�q�̃��u�̌��]�O���j3�~1018�� ���x���`2�� �\�Ɏ����B
�N�G�[�T�[�̒��S���̌��q���́A���z�̎��ʂ�104�{�����z�̎��ʂ�105�{�����z�̎��ʂ�106�{�����z�̎��ʂ�107�{�����z�̎��ʂ�108�{�����z�̎��ʂ�109�{�Ƒ�������B ���̎��̃N�G�[�T�[�̒��S���̏�Ԃ͕\�̂悤�ɂȂ��Ă���B �����A�N�G�[�T�[�̒��S���̎��ʂ����z��104�{�ɐ��������A�d�q�̃��u�̌��]�O����1.135�~10�|16���ɂȂ�A�d�q�̃��u�̃G�l���M�[��7.634�~10�|8�i�ɂȂ�A�W�F�b�g�̓͂�������1.310�~1011�j���ɂȂ�A������1��3�̌��q����6.838�~1017�ɂȂ�A���x��8.686�~1011���ɂȂ�B �X�ɁA�N�G�[�T�[�̒��S���̓d�q�̃��u�̃G�l���M�[�͑傫���Ȃ�A�W�F�b�g�̓͂������������Ȃ�A��������̌��f���W�߂�B �N�G�[�T�[�̒��S���̎��ʂ����z��105�{�ɐ��������A�d�q�̃��u�̌��]�O����5.269�~10�|17���ɂȂ�A�d�q�̃��u�̃G�l���M�[��1.645�~10�|7�i�ɂȂ�A�W�F�b�g�̓͂�������3.065�~1011�j���ɂȂ�A���S����1��3�̌��q����6.837�~1017�ɂȂ�A���x��4.032�~1012���ɂȂ�B �P�T�D�@�F���̎����d�q�̃��u�̌��]�O���ŕ\�����ꍇ�A����̌��q���W�܂��Ăł�����͉̂����B �E10�|17���̎���A���q�̂`�́A�`��1.058�~10�|10����10�|17����1.058�~107�ł��B ����́A���S�����z�̎��ʂ̉��{�̃N�G�[�T�[�̂`���B���{�̎��ʂ��Ƃ��܂��ƁA �N�G�[�T�[�̂`��4.325�~104�~��1/3�ł�����A 1.058�~107��4.325�~104�~��1/3 ��1/3��1.058�~107���i4.325�~104�j��2.446�~102 �����i2.446�~102�j3��1.463�~107 10�|17���̎���A���q���W�܂��āA���S�����z�̎��ʂ�1.463�~107�{�̃N�G�[�T�[���ł���B �E10�|16���̎���A���q�̂`�́A�`��1.058�~10�|10����10�|16����1.058�~106�ł��B ����́A���S�����z�̎��ʂ̉��{�̃N�G�[�T�[�̂`���B���{�̎��ʂ��Ƃ��܂��ƁA �N�G�[�T�[�̂`��4.325�~104�~��1/3�ł�����A 1.058�~106��4.325�~104�~��1/3 ��1/3��1.058�~106���i4.325�~104�j��2.446�~10 �����i2.446�~10�j3��1.463�~104 10�|16���̎���A���q���W�܂��āA���S�����z�̎��ʂ�1.463�~104�{�̃N�G�[�T�[���ł���B �E10�|15���̎���A���q�̂`�́A�`��1.058�~10�|10����10�|15����1.058�~105�ł��B ����́A���S�����z�̎��ʂ̉��{�̐��̂`���B���{�̎��ʂ��Ƃ��܂��ƁA ����1.058�~105�����z�̒��S�̂`��1.058�~105���i3.872�~103�j��2.732�~10 10�|15���̎���A���q���W�܂��āA���S�����z�̎��ʂ�2.732�~10�{�̐����ł���B �E10�|14���̎���A���q�̂`�́A�`��1.058�~10�|10����10�|14����1.058�~104�ł��B ����́A���S�����z�̎��ʂ̉��{�̐��̂`���B���{�̎��ʂ��Ƃ��܂��ƁA ����1.058�~105�����z�̒��S�̂`��1.058�~105���i3.872�~104�j��2.732 10�|14���̎���A���q���W�܂��āA���S�����z�̎��ʂ�2.732�{�̐����ł���B �P�U�D�@�W�F�b�g�������������A���̏�ɂł�����͉̂����B 10�|17���̎���A�W�F�b�g������������ɂł�����̂̓N�G�[�T�[�̒��S�ł��B 10�|16���̎���A�W�F�b�g������������ɂł�����̂͐��ł��B 10�|15���̎���A�W�F�b�g������������ɂł�����̂͏��f���ł��B �W�F�b�g������������ɗL�������q�̂`���ǂꂮ�炢�ł��邩�ɂ���āA�ł�����̂��قȂ�B �E10�|17���̎���A�W�F�b�g������������ɗL�������q�́A10�|16���̌��q���Ƃ���B 10�|16���̌��q���W�܂��āA���S�����z�̎��ʂ�1.463�~104�{�̃N�G�[�T�[���ł��邱�ƂɂȂ�܂��B �������A���̏��1��3�̌��q����1018�Ȃ̂ŁA10�|15���̏�̌��q�Z�x��103�{�Ȃ̂ŁA�N�G�[�T�[�̎��ʂ�103�{�ɂȂ�A���S�����z�̎��ʂ�1.463�~105�{�̃N�G�[�T�[���ł��邱�ƂɂȂ�܂��B �E10�|16���̎���A�W�F�b�g������������ɗL�������q�́A10�|15���̌��q���Ƃ���B 10�|15���̌��q���W�܂��āA���S�����z�̎��ʂ�2.732�~10�{�̐����ł��邱�ƂɂȂ�܂��B �E10�|15���̎���A�W�F�b�g������������ɗL�������q�́A10�|14���̌��q���Ƃ���B 10�|14���̌��q���W�܂��āA���S�����z�̎��ʂ�2.732�{�̐����ł��邱�ƂɂȂ�܂��B �������A���̏��1��3�̌��q����1012�Ȃ̂ŁA���ʂ�1000����1�ɂȂ�A���͂ł������f�����ł���B �E10�|14���̎���A�W�F�b�g������������ɗL�������q�́A10�|13���̌��q���Ƃ���B 10�|13���̌��q���W�܂��āA���S�����z�̎��ʂ�0.2732�{�̘f�����ł��邱�ƂɂȂ�܂��B �������A���̏��1��3�̌��q����109�Ȃ̂ŁA���ʂ�106����1�ŁA�f���͂ł������f�����ł���B �P�V�D�@�N�G�[�T�[�̑傫���͂�����ł��������B�N�G�[�T�[��1��]���鎞�A���������邩�B�i2007�N9��28���ɒ�o�����A����2007�|279617�D�j �Q����̘͂r�́A�N�G�[�T�[����͂ɐ��������A�W�F�b�g�̓͂����ɂł������̏W�c�ł��B �Q����̘͂r�̑傫���́A��͂̒��a�ł��B �����A��͂̒��a�́A�N�G�[�T�[���ł������A�W�F�b�g���͂������ł��B ��͂̒������̌����Ȃ��Ă��镔���́A�N�G�[�T�[�ł����������ł��B ��͂̒��a��10�����N�Ƃ��܂��B ��͂̌����Ȃ��������̒�����3000���N�Ƃ��܂��B 2007�N8��25���ɒ�o���������肢�́u������26�v����A�N�G�[�T�[�̎��ʂƃW�F�b�g���͂�����������܂��B
�N�G�[�T�[�̑傫���F2�~�W�F�b�g���͂������͂����炩�B �N�G�[�T�[�̑傫���F2�~�W�F�b�g���͂������́A��͂̌����Ȃ��������̒����F��͂̒��a�ł��B ��͂̌����Ȃ��������̒����F��͂̒��a��3000���N�F105���N��1�F33.33 ����ŁA�N�G�[�T�[�̑傫���F2�~�W�F�b�g���͂�������1�F33.33�ł��B �N�G�[�T�[�̑傫���F2�~�W�F�b�g���͂�������1�F33.33 �N�G�[�T�[�̑傫����2�~�W�F�b�g���͂�������33.33���W�F�b�g���͂������~0.06 �N�G�[�T�[�̑傫�����W�F�b�g���͂������~0.06 �@ �N�G�[�T�[�̎��ʂ����z��104�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������1.310�~1014���ł�����A �N�G�[�T�[�̑傫����1.310�~1014���~0.06��7.86�~1012�� �N�G�[�T�[�̑傫����7.86�~1012���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 7.86�~1012���~3.14���i3�~108���~24�~60�~60�j��9.522�~10�|1 �N�G�[�T�[��1��]����ƁA0.95��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i7.86�~1012���j��3000�~9.46�~1015�����i7.86�~1012���j��3.611�~106�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~1.310�~1014���j��105�~9.46�~1015�����i2�~1.310�~1014���j��3.611�~106�{�Ɋg�債���B �A �N�G�[�T�[�̎��ʂ����z��105�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������3.065�~1014���ł�����A �N�G�[�T�[�̑傫����3.065�~1014���~0.06��1.839�~1013�� �N�G�[�T�[�̑傫����1.839�~1013���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 1.839�~1013���~3.14���i3�~108���~24�~60�~60�j��2.228 �N�G�[�T�[��1��]����ƁA2.2��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i1.839�~1013���j��3000�~9.46�~1015�����i1.839�~1013���j��1.543�~106�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~3.065�~1014���j��105�~9.46�~1015�����i2�~3.065�~1014���j��1.543�~106�{�Ɋg�債���B �B �N�G�[�T�[�̎��ʂ����z��106�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������6.6�~1014���ł�����A �N�G�[�T�[�̑傫����6.6�~1014���~0.06��3.96�~1013�� �N�G�[�T�[�̑傫����3.96�~1013���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 3.96�~1013���~3.14���i3�~108���~24�~60�~60�j��4.797 �N�G�[�T�[��1��]����ƁA4.8��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i3.96�~1013���j��3000�~9.46�~1015�����i3.96�~1013���j��7.167�~105�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~6.6�~1014���j��105�~9.46�~1015�����i2�~6.6�~1014���j��7.167�~105�{�Ɋg�債���B �C �N�G�[�T�[�̎��ʂ����z��107�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������1.422�~1015���ł�����A �N�G�[�T�[�̑傫����1.422�~1015���~0.06��8.532�~1013�� �N�G�[�T�[�̑傫����8.532�~1013���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 8.532�~1013���~3.14���i3�~108���~24�~60�~60�j��1.034�~10 �N�G�[�T�[��1��]����ƁA10��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i8.532�~1013���j��3000�~9.46�~1015�����i8.532�~1013���j��3.326�~105�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~1.422�~1015���j��105�~9.46�~1015�����i2�~1.422�~1015���j��3.326�~105�{�Ɋg�債���B �D �N�G�[�T�[�̎��ʂ����z��108�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������3.065�~1015���ł�����A �N�G�[�T�[�̑傫����3.065�~1015���~0.06��1.839�~1014�� �N�G�[�T�[�̑傫����1.839�~1014���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 1.839�~1014���~3.14���i3�~108���~24�~60�~60�j��2.228�~10 �N�G�[�T�[��1��]����ƁA22��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i1.839�~1014���j��3000�~9.46�~1015�����i1.839�~1014���j��1.543�~105�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~3.065�~1015���j��105�~9.46�~1015�����i2�~3.065�~1015���j��1.543�~105�{�Ɋg�債���B �E �N�G�[�T�[�̎��ʂ����z��109�{�̏ꍇ�B �E�N�G�[�T�[�̑傫���͂����炩�B �W�F�b�g���͂�������6.6�~1015���ł�����A �N�G�[�T�[�̑傫����6.6�~1015���~0.06��3.96�~1014�� �N�G�[�T�[�̑傫����3.96�~1014���ł��B �E�N�G�[�T�[��1��]���鎞�A���������邩�B �N�G�[�T�[�̎��]����b����3�~108���Ƃ���B 3.96�~1014���~3.14���i3�~108���~24�~60�~60�j��4.797�~10 �N�G�[�T�[��1��]����ƁA48��������B �E�N�G�[�T�[�͉��{�Ɋg�債�����B2�~�W�F�b�g���͂��������͉��{�Ɋg�債�����B �N�G�[�T�[�́A3000���N�ɂȂ����̂ŁA 3000���N���i3.96�~1014���j��3000�~9.46�~1015�����i3.96�~1014���j��7.167�~104�{�Ɋg�債���B 2�~�W�F�b�g���͂��������́A��͂̒��a�ɂȂ����̂ŁA 105���N���i2�~6.6�~1015���j��105�~9.46�~1015�����i2�~6.6�~1015���j��7.167�~104�{�Ɋg�債���B �܂Ƃ߂ĕ\�ɂ���B
���̎��ɂ���āA���������ł��邩�B 1. �N�G�[�T�[��1���]�͐����ł���Ƃ����܂��B���̏ꍇ�A���S�̎��ʂ����z��106�{�̃N�G�[�T�[�ł��B 2. ��͌n�̒��S�̃u���b�N�z�[���͑��z�̎��ʂ�106�{�ł��邩��A�N�G�[�T�[�̒��S���̎��ʃG�l���M�[�͑��z���ʃG�l���M�[��106�{2��108�{�ł���A�N�G�[�T�[�́A1.543�~105�{�Ɋg�債��͌n�ɂȂ����B 3. �N�G�[�T�[��1���]�������ł��鎖�ɂ���āA�W�F�b�g�̓͂������͐������B 4. �W�F�b�g�̓͂����������z�̐ԓ����a�~849�~�N�G�[�T�[���͂̒��S�̂`�����z�̒��S�̂`��6.96�~105�j���~849�~�N�G�[�T�[���͂̒��S�̂`���i3.872�~103�j��1.526�~105�j���~�N�G�[�T�[���͂̒��S�̂` ���̎��͐������B����́A2007�N8��25���ɒ�o����������́u������24�v�ɋL�����B 5. ���S�������z�̎��ʂ̃��{�̃N�G�[�T�[�̏ꍇ�A �N�G�[�T�[�̒��S�̂`��4.325�~104�~��1/3 ���̎��͐������B����́A2007�N8��25���ɒ�o����������́u������22�v�ɋL�����B �P�W�D�@�u���b�N�z�[���̂`��7.378�~105�ŁA�W�F�b�g�͔��a1.126�~1011�j���܂œ͂��܂��B���̃W�F�b�g�ɂ���Ăł���N�G�[�T�[�̑傫���͂����炩�B���̃N�G�[�T�[��1���]����Ƃ��̓����͂����炩�B�i2007�N9��28���ɒ�o�����A����2007�|279617�D�j �N�G�[�T�[�̑傫����2�~�W�F�b�g���͂�������33.3���W�F�b�g���͂������~0.06��1.126�~1011�j���~0.06��6.756�~109�j����6.756�~1012�� �N�G�[�T�[�̑傫���́A���a6.756�~1012���ł��B ���̃N�G�[�T�[��1�]����Ƃ��̓����͂����炩�B���]����b����3�~108���Ƃ���B 3.14�~6.756�~1012�����i3�~108���~24�~60�~60�j��8.184�~10�|1�i���j �N�G�[�T�[��1�]����Ƃ��̓����́A0.818���ł��B ���̎��ɂ���ĉ��������ł��邩�B 1. �N�G�[�T�[�̑傫���͐�����1���]����B�������A�u���b�N�z�[���̃W�F�b�g�łł���N�G�[�T�[��0.818����1���]����傫���ł��B 2. ���̎��́A�N�G�[�T�[�̓u���b�N�z�[���̃W�F�b�g���͂����a1.126�~1011�j���܂ł͈̔͂��N�G�[�T�[�ɐ������̂ł͂Ȃ��B�����Ƒ傫���͈͂��N�G�[�T�[�ɐ������B 3. �N�G�[�T�[���ł������A�F���̌��q���x�i���̎��͌��q�Ƃ��đ��݂����A�d�q�̃��u�Ɨz�q�̃��u�͒P�Ƃő��݂����B�j�͋ψ�ł������B 4. �������A�N�G�[�T�[�̑傫�����قȂ�̂́A�N�G�[�T�[���ł�����̃G�l���M�[���قȂ邽�߂ł���B �P�X�D�@�N�G�[�T�[����o���������q�̃G�l���M�[�́A�ǂ̂悤�ł��邩�B�i2007�N9��28���ɒ�o�����A����2007�|279617�D�j �N�G�[�T�[�̌��q��1010���N�̏ꂩ��o�����܂��B���̌��q�������Ƃ��ē������邽�߂ɂ́A���q�̃G�l���M�[��6.31�~10�|17�i�łȂ�������܂���B �������A���̏�́A�d�q�̃��u�̌��]�O����10�|16���ł�����A1���]�łł���d�C�̌��q�̋O����10�|16���ł��B 10�|16���̏�̓d�C�̌��q1�̃G�l���M�[�́A 10�|41�i����10�|16����10�|25�i 6.31�~10�|17�i�ɐ��邽�߂ɂ͉��̓d�C�̌��q���W�܂�Ȃ���ΐ���Ȃ����B 6.31�~10�|17�i��10�|25�i��6.31�~108�W�܂�Ȃ���ΐ���Ȃ��B ����ŁA�N�G�[�T�[����o������d�C�̌��q�́A6.31�~108�W�܂��Ēn�\�ɂ��ǂ蒅�������Ɛ����Ă���B �����A108�W�܂��đ����Ă���̂ł���A���̃G�l���M�[�́A 10�|25�i�~108��10�|17�i�ł��B 6.31�~10�|17�i�ŏo������ƁA6.67�~10�|35�i�ɐ��肽�ǂ蒅���̂ł�����A10�|17�i�ŏo������ƁA 6.67�~10�|35�i��6.31��1.057�~10�|35�i�ł��ǂ蒅���܂��B ���̋O���́A10�|41�i�����i1.057�~10�|35�i�j��9.461�~10�|7���ŁA ���̔g���́A9.461�~10�|7���~2��1.892�~10�|6���ł��B 1.892�~10�|6���̔g���́A�ߐԊO���ł��B ������A�]�����Ŋώ@�ł��܂��B ���̎��ɂ���ĉ��������ł��邩�B �N�G�[�T�[����o������d�C�̌��q��108���ɂȂ��đ����Ă���B �Q�O�D�@�N�G�[�T�[�͂ǂ̂悤�ɋ�͂ɕω��������B�i2007�N9��28���ɒ�o�����A����2007�|279617�D�j ����́A�u�X�v�Ɏ������l���ł��B ��͌n�𒆐S�ɍl����B �N�G�[�T�[�ɂ͐����ł���͌n�̒������ɐ������B �W�F�b�g���͂������ɂ������ł��A��͌n�̘r�ɐ������B ��͌n�̒��S�̃u���b�N�z�[���́A���z�̎��ʂ�106�{�ł��B ����ŁA�N�G�[�T�[���������̃N�G�[�T�[�̒��S�̎��ʃG�l���M�[�́A���z�̎��ʃG�l���M�[��106�{2��10�W�{�ł��B �N�G�[�T�[�̑傫���́A1.839�~1014������A�o�W���̑傫��3000���N�i2.838�~1019���j�ɂȂ����B 2�~�W�F�b�g���͂������́A2�~3.065�~1015������A��͌n�̒��a10�����N�i9.46�~1020���j�ɂȂ����B 1.543�~105�{�ɂȂ����B �N�G�[�T�[��1.543�~105�{�Ɋg�債�A��͌n�ɂȂ����B �y�}�ʂ̊ȒP�Ȑ����z �y�}1�z�N�G�[�T�[�ƃW�F�b�g�̓͂��������̕��ʐ}�Ƌ�͌n�̕��ʐ}�B �N�G�[�T�[�ƃW�F�b�g�̓͂��������̗��ʐ}�Ƌ�͌n�̗��ʐ}�B ��͌n�̒�����3000���N�B�r�̑傫����10�����N�ł��B �y�����̐����z �P�@�N�G�[�T�[ �Q�@�W�F�b�g���͂������� �R�@��͌n�̒��S�� �S�@��͌n�̘r �y�}1�z 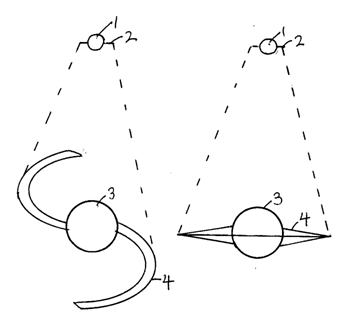 �Q�P�D�@�N�G�[�T�[��105�N�Ԃɉ��{�Ɋg�債�����B�i2007�N9��28���ɒ�o�����A����2007�|279617�D�u������14�v�j �N�G�[�T�[�́A136���N�ԂŁA1.839�~1014������A2.838�~1019���Ɋg�債���B 105�N�Ԃɂ��{�g�債���Ƃ���B 1.839�~1014���~���~136�~108�|5�N��2.838�~1019�� ����2.838�~1019�����i1.839�~1014���~136�~103�N�j��1.135 �N�G�[�T�[�́A105�N�Ԃ�1.135�{�Ɋg�債���B 2�~�W�F�b�g���͂������́A105�N�Ԃ�1.135�{�Ɋg�債���B 136���N�ʼn����ɂȂ邩�B2�~�W�F�b�g���͂������́A2�~3.065�~1015���ł��B 2�~3.065�~1015���~1.135�~136�~108�|5�N��9.46�~1020�� ����āA�N�G�[�T�[��W�F�b�g���͂��������́A105�N�Ԃ�1.135�{�Ɋg�債���B �Q�Q�D�@��͂̒��S�̃u���b�N�z�[���̎��ʂ����z���ʂ�10���{�̏ꍇ�A�F���̋O���G�l���M�[�̎��́A5.438�~1018�{2n/3J�E�j���ł��B�O���̃G�l���M�[��5.438�~1018�{2n/3J�E�j�����������O���̑��x2�A���̎�����A�N�G�[�T�[����̃N�G�[�T�[��W�F�b�g���͂��O���̃G�l���M�[�Ƒ��x�����߂�B�i2008�N3��27���ɒ�o�����A����2008�|113159�D�j �N�G�[�T�[����A�N�G�[�T�[�̒��S�̃u���b�N�z�[���̎��ʃG�l���M�[�́A���z���ʃG�l���M�[��108�{�ł��B �N�G�[�T�[�̑傫���́A1.839�~1014���ł��B1.839�~1011�j���ł��B �W�F�b�g���͂�������3.065�~1015���ł��B �@�N�G�[�T�[�̒��S����1.839�~1011�j���̋O���̃G�l���M�[�Ƒ��x�͂����炩�B �N�G�[�T�[�̒��S�̃u���b�N�z�[���̎��ʃG�l���M�[�́A���z���ʃG�l���M�[��108�{�ł��B �O���̃G�l���M�[��5.438�~1018�{2n/3J�E�j�����������O���̑��x2 �O���̃G�l���M�[��5.438�~1018�{2�~8/3J�E�j����(1.839�~1011�j��)��2.957�~107�~105.33�i��2.957�~107�~105�~100.33�i��2.957�~1012�~2.15�i��6.358�~1012�i �O���̑��x2��6.358�~1012 �O���̑��x��(6.358�~1012)1/2=2.521�~106(Km/s) �N�G�[�T�[�̒��S����1.839�~1011�j���̋O���̃G�l���M�[��6.358�~1012�i�ŁA���x��2.521�~106Km/s�ł��B ����͌����ȏ�ł��B �A�N�G�[�T�[�̎���A�W�F�b�g���͂�����3.065�~1012�j���̋O���̃G�l���M�[�Ƒ��x�͂����炩�B �O���̃G�l���M�[��5.438�~1018�{2n/3J�E�j�����������O���̑��x2 �O���̃G�l���M�[��5.438�~1018�{2�~8/3J�E�j����(3.065�~1012�j��)��1.774�~106�~105.33�i��1.774�~106�~105�~100.33�i��1.774�~1011�~2.15�i��3.814�~1011�i �O���̑��x2��3.814�~1011 �O���̑��x��(3.814�~1011)1/2=(38.14�~1010)1/2=6.176�~105(Km/s) �N�G�[�T�[�̎���A�W�F�b�g���͂�����3.065�~1012�j���̋O���̃G�l���M�[��3.814�~1011�i�ŁA���x��6.176�~105Km/s�ł��B ����͌����ȏ�ł��B
�Q�R�D�@�N�G�[�T�[�̂ǂ̕�������͂̂ǂ̕����ɂȂ������B�i2008�N9��1���ɒ�o�����A����2008�|223099.�j �N�G�[�T�[�́A�N�G�[�T�[�̋��́{�r�̋O���A�łł��Ă���B ��͂́A���S�j�o���W�{3�L���p�[�Z�N�̘r�{�r�A�łł��Ă���B �E�N�G�[�T�[�̂ǂ̕�������͂̂ǂ̕����ɂȂ������B �P�[�T�[�̋��̂́A��͂̒��S�j�o���W�ɐ������B���S�j�o���W�͒��S����6000���N�ł��B �N�G�[�T�[�̘r�̋O���́A�r�ɐ������B �����\�Ɏ����B
�Q�S�D�@�N�G�[�T�[����͌n�ɂȂ�A���̂���~�Տ�ɂȂ����̂͂ǂ����Ă��B���z�̐e�ł����1����̐��̎��͂͐��f�̋��̂ł������B���ꂪ���R�[�h��ɂȂ����̂͂ǂ����Ă��B���z�n�̘f���́A�e�ł����1����̐��̒��V�������ɂ���ċ���ɔ�U�������f�łł����̂ɁA���R�[�h��ɕ���ł���̂͂ǂ����Ă��B(2008�N10��17���ɒ�o�����A����2008�|268538�D) ���̂��~�Տ�ɂȂ������R�́A���S�̃u���b�N�z�[�������O�����x�������Ō��]�ł���������ł��B�O���͌��]�^�������܂��B����ŁA�O���ɋ���ɔ�U�������f�͌��]�O��������]����B ���̎��ɂ���āA���͉̂~�Տ�ɂȂ�B ���N�G�[�T�[����͌n�ɂȂ��ċ��̂���~�Տ�ɂȂ����̂͂ǂ����Ă��B �N�G�[�T�[�̒��S�̓u���b�N�z�[���ł��B���̃u���b�N�z�[�����N�G�[�T�[�̋O���G�l���M�[�����B�O���G�l���M�[�͑��x�����B ���̎��́A�O���G�l���M�[�����]���x2��5.4�~1018�~102n/3J�EKm�����a�A�ł��B 10n��10n���z���ʂł��B �E�N�G�[�T�[�����O���̃G�l���M�[�����]���x2�͂����炩�B �N�G�[�T�[�̎��ʂ�6�~1011���z���ʂƂ���B6�~1011��100.7782�{11��1011.7782 �N�G�[�T�[�����O���G�l���M�[�����]���x2��5.4�~1018�~102n/3J�EKm�����a��5.4�~1018�~102�~11.7782/3J�EKm�����a��5.4�~1018�~107.852J�EKm�����a��5.4�~1018�{7�~100.852J�EKm�����a��5.4�~1025�~7.083J�EKm�����a��3.825�~1026J�EKm�����a �N�G�[�T�[�����O���̃G�l���M�[�����]���x2��3.825�~1026J�EKm�����a �E�N�G�[�T�[�����O���̃G�l���M�[�����]���x2��3.825�~1026J�EKm�����a�A�̎��ɂ��A�N�G�[�T�[�̔��a�̌��]���x�����߂�B ���]���x��(3.825�~1026J�EKm�����a)1/2 �E���]���x�������ł��锼�a�͂����炩�B ���]���x��(3.825�~1026J�EKm�����a)1/2��3�~105Km 3.825�~1026J�EKm�����a��9�~1010Km ���a��3.825�~1026J�EKm��(9�~1010Km)��4.25�~1015Km �N�G�[�T�[�̒��S����A���a4.25�~1015Km�̋O���͌����ł��B �E���݁A��͌n�̔��a��5�~104���N�ł��B 10�|16������̑傫���́A���݂̑傫����7.851�~10�|5�{�ł��B���̎��ɂ��āA���́A����2008�|223099�̢������15��ɋL�����B ����āA10�|16������A��͌n�̑傫���́A5�~104�~9.46�~1012Km�~7.851�~10�|5��3.714�~1013Km�ł����B ����ŁA���̋O���͌����ł��B 10�|16������A�N�G�[�T�[�͌����ł��B ���̂悤�ɁA�N�G�[�T�[�̋��̂���͌n�̉~�Տ�ɂȂ����̂́A�O���̌��]���x�������ł���������ł��B �����z�̐e�ł����1����̐��̋O�������烌�R�[�h��ɂȂ����̂͂ǂ����Ă��B ���z�̐e�ł����1����̐��̒��S�ɑ��݂����u���b�N�z�[�����畬�o�����W�F�b�g�́A���̂̋�Ԃ���_�[�N�}�^�[���W�ߐ��f�Ƃ����B����ŁA���z�̐e�ł����1����̐��̎��͂͐��f�̋��̂ł������B���ꂪ���z�n�Ɠ����悤�Ƀ��R�[�h��ɂȂ����B ����́A���z�̐e�ł����1����̐��̒����ɑ��݂���u���b�N�z�[�������O���̌��]���x�������ł���������ł��B ���z�̐e�ł����1����̐��̎��ʂ́A���z���ʂ�8.246�{�ł��B���̎��ɂāA���́A����2007�|150959�̢�������V��ɋL�����B ���z���ʂ�8.246�{�́A100.9162�ł��B ���z�̐e�ł����1����̐��̒��S�ɑ��݂����u���b�N�z�[�������O���G�l���M�[�����]���x2��5.4�~1018�~102�~0.9162/3J�EKm�����a��5.4�~1018�~100.6108J�EKm�����a��5.4�~1018�~4.081J�EKm�����a��2.204�~1019J�EKm�����a ���z�̐e�ł����1����̐��̒��S�ɑ��݂����u���b�N�z�[�������O���G�l���M�[�����]���x2��2.204�~1019J�EKm�����a ���]���x��(2.204�~1019J�EKm�����a)1/2 �E�����ɂȂ锼�a�͂����炩�B ���]���x��(2.204�~1019J�EKm�����a)1/2��3�~105Km 2.204�~1019J�EKm�����a��(3�~105Km)2 ���a��2.204�~1019J�EKm��(9�~1010Km)��2.449�~108Km ��1����̐��̒��S����A2.449�~108Km�͌����ł��B ���̋����͉ΐ��̋����ɋ߂��B �E�j�Z���������N�����W�F�b�g���͂��O���ɂł����g���f�̏��f���h�B�̌��]���x�͂����炾�������B �j�Z���������N�����W�F�b�g���͂����a�����z�̔��a�~849�~�j�Z���̏�̂`���j�Z���̏�̂`��6.96�~105�j���~849�~1��5.9�~108�j�� ���̋O���̌��]���x�́A ���]���x���o2.204�~1019J�EKm��(5.9�~108Km)�p1/2��(3.736�~1010J)1/2��1.933�~105Km�ł����B �j�Z���������N�����W�F�b�g���͂��O���ɂł����g���f�̏��f���h�B�̌��]���x�́A1.933�~105Km�ł����B �E�I���g�[�̉_�ɂȂ������f�_�����݂���O���̌��]���x�͂����炾�������B �I���g�[�̉_���ł��������́A �W�F�b�g���͂�������(���a)�����z�̔��a�~849�~�u���b�N�z�[���̂`���j�Z���̏�̂`��6.96�~105�j���~849�~7.375�~105��(3.873�~103)��1.125�~1011�j���ł��B ���̋O���̌��]���x�́A ���]���x���o2.204�~1019J�EKm��(1.125�~1011�j��)�p1/2��(1.959�~108J)1/2��1.399�~104Km �I���g�[�̉_�ɂȂ������f�_�����݂���O���̌��]���x�́A1.4�~104Km�ł��B ���̍l���ł��ƁA�I���g�[�̉_�́A�~�Տ�ɑ��݂��邱�ƂɂȂ�B ���̂悤�ɁA���z�̐e�ł����1����̐��̒��S�ɑ��݂����u���b�N�z�[�������A�O���̌��]���x�͍����ł������̂ŁA���̂��烌�R�[�h�ɂȂ����B �����z�n�̘f���́A�e�ł����1����̐��̒��V�������ɂ���ċ���ɔ�U�������f�łł����̂ɁA���R�[�h��ɕ���ł���̂͂ǂ����Ă��B(����͢������1��Əd�����܂��B) ���z�̒��S�͒����q���ł����B���̒����q�������z�n�̋O���G�l���M�[��������B�O���G�l���M�[�͌��]���x��������B ���z�̎��ʂ�1���z���ʂł�����A�P��100�ł��B ���z�̒��S�ɑ��݂��������q����������O���G�l���M�[�����]���x2��5.4�~1018�~102�~0/3J�EKm�����a��5.4�~1018J�EKm�����a ���z�̒��S�ɑ��݂��������q����������O���G�l���M�[�����]���x2��5.4�~1018J�EKm�����a ���]���x��(5.4�~1018J�EKm�����a)1/2 �E�����ɂȂ锼�a�͂����炩�B ���]���x��(5.4�~1018J�EKm�����a)1/2��3�~105Km 5.4�~1018J�EKm�����a��(3�~105Km)2 ���a��5.4�~1018J�EKm��(9�~1010Km)��6�~107Km �����ɂȂ锼�a�́A6�~107Km�ł��B ���̋����͐����̋����ɋ߂��B ����ł́A�f�����ł����O���̌��]���x�͂����炾�������B �������ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(0.579�~108Km)�p1/2��(9.326�~1010J)1/2��3.054�~105Km �����̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(1.082�~108Km)�p1/2��(4.991�~1010J)1/2��2.234�~105Km �n���̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(1.496�~108Km)�p1/2��(3.610�~1010J)1/2��1.900�~105Km �ΐ��̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(2.279�~108Km)�p1/2��(2.369�~1010J)1/2��1.539�~105Km �ؐ��̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(7.783�~108Km)�p1/2��(6.938�~109J)1/2��8.329�~104Km �y���̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(14.294�~108Km)�p1/2��(3.778�~109J)1/2��6.147�~104Km �V�����̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(28.750�~108Km)�p1/2��(1.879�~109J)1/2��4.335�~104Km �C�����̂ł����O���̌��]���x�͂����炾�������B ���]���x���o5.4�~1018J�EKm��(45.044�~108Km)�p1/2��(1.199�~109J)1/2��3.463�~104Km �f�������݂���悤�ɂȂ�O���̌��]���x�́A������̏ꍇ�ɂ��A�����ł����B �E�j�Z���������N�����W�F�b�g���͂��O���ɂł������f���B�̌��]���x�͂����炾�������B �j�Z���������N�����W�F�b�g���͂����a�����z�̔��a�~849�~�j�Z���̏�̂`���j�Z���̏�̂`��6.96�~105�j���~849�~1��5.9�~108�j�� ���̋O���̌��]���x�́A ���]���x���o5.4�~1018J�EKm��(5.9�~108Km)�p1/2��(0.9153�~1010J)1/2��0.957�~105Km��9.57�~104Km�ł����B �j�Z���������N�����W�F�b�g���͂��O���ɂł������f���B�̌��]���x�́A9.57�~104Km�ł����B �E�G�b�W���[�X�E�J�C�p�[�x���g���ł����O���̌��]���x�͂����炾�������B �W�F�b�g���͂�������(���a)�����z�̔��a�~849�~�����q���̂`���j�Z���̏�̂`��6.96�~105�j���~849�~1.968�~105��(3.873�~103)��3�~1010�j�� ���̋O���̑��x�́A ���x���o5.4�~1018J�EKm��(3�~1010Km)�p1/2��(1.8�~108J)1/2��1.342�~104Km �G�b�W���[�X�E�J�C�p�[�x���g���ł����O���̌��]���x�́A1.342�~104Km�ł����B ���̂悤�ɁA���z�̒��S�̒����q�������A���z���̌��]���x�͍����ł������̂ŁA���̂ɔ�U�������f�̓��R�[�h��ɂȂ����B �܂Ƃ߂ĕ\�Ɏ����B
���z�̒��S�̒����q�������A�f���̋O���̌��]���x�B����͢������1��ɋL�����B
|