１．　ブラックホールについて。（2007年4月18日に提出した、特願2007−133476．の「請求項６」）

ブラックホールを次の2点から考える。

�@    ブラックホールは、太陽の質量の30倍の星が爆発した後に残る、高エネルギーの中央部が収縮したものです。

この星の中央部の温度は、

太陽の中央部の温度×30²＝15×10⁶℃×900＝1.35×10¹⁰℃です。

この星の中央の万有引力係数は、

6.672×10⁻¹¹Jm/Kg²×1.35×10¹⁰＝9×10⁻¹Jmです。

しかし、ブラックホールになると、更に収縮するので、その収縮を10^1/2としますと、ブラックホールの場の万有引力係数は、9×10⁻¹Jm×10＝9Jm/Kg²です。

このブラックホールの性質。

温度は、1.35×10¹⁰℃×10＝1.35×10¹¹℃です。

Aは、（1.35×10¹¹℃）^1/2=13.5^1/2×10⁵＝3.674×10⁵です。

万有引力定数は、9Jm/Kg²です。

電子のラブの公転軌道は、1.058×10⁻¹⁰m÷（3.674×10⁵）＝2.88×10⁻¹⁶ｍです。

電子のラブのエネルギーは、8.187×10⁻¹⁴J×3.674×10⁵=3.008×10⁻⁸Jです。

陽子のラブの公転軌道は、5.764×10⁻¹⁴ｍ÷（3.674×10⁵）＝1.569×10⁻¹⁹ｍです。

陽子のラブのエネルギーは、1.5×10⁻¹⁰J×3.674×10⁵=5.511×10⁻⁵Jです。

ラブの軌道エネルギーは、8.665×10⁻²⁴Jmです。

光子の公転軌道エネルギーは、1.233×10⁻⁴¹Jmです。

光子の自転軌道エネルギーは、6.112×10⁻⁵⁷Jmです。

1電子のラブが1秒間に作る、熱と成る電気の光子のエネルギーは、

1.233×10⁻⁴¹Jm÷（2.066×10⁻⁵ｍ）×6.336×10¹⁵公転×3.674×10⁵＝3.781×10⁻²¹J×3.674×10⁵＝3.674×10⁵℃です。

1電子のラブが1秒間に作る、引力と成る磁気の光子のエネルギーは、

1.233×10⁻⁴¹Jm÷｛2.066×10⁻⁵ｍ÷(3.674×10⁵)｝×6.336×10¹⁵公転＝1.389×10⁻¹⁵J、です。

�A    太陽の質量をブラックホールにすると、半径３Kmになります。

太陽の半径は約70万Kmです。

重力（万有引力）＝GｍM÷ｒ²但し、G=重力定数、ｍとM＝夫々の質量、ｒ＝物体間の距離。

質量は同じですから、重力の比は、

太陽：ブラックホール＝3²：（7×10⁵）²＝9：49×10¹⁰＝１：5.444×10¹⁰

太陽の重力は、地表の重力の10倍ですから、

地表の重力：ブラックホールの重力＝１：10×5.444×10¹⁰＝１：5.444×10¹¹です。

それで、

ブラックホールのA=（引力）^1/2=（5.444×10¹¹）^1/2=54.44^1/2×10⁵＝7.378×10⁵です。

このブラックホールの性質。

Aは、7.378×10⁵です。

温度は、（7.378×10⁵）²℃＝5.444×10¹¹℃です。

万有引力定数は、6.672×10⁻¹¹Jm/Kg²×5.444×10¹¹＝36.322Jm/Kg²です。

電子のラブの公転軌道は、1.058×10⁻¹⁰m÷（7.378×10⁵）＝1.434×10⁻¹⁶ｍです。

電子のラブのエネルギーは、8.187×10⁻¹⁴J×7.378×10⁵=6.040×10⁻⁸Jです。

陽子のラブの公転軌道は、5.764×10⁻¹⁴ｍ÷（7.378×10⁵）＝4.253×10⁻²⁰ｍです。

陽子のラブのエネルギーは、1.5×10⁻¹⁰J×7.378×10⁵=1.107×10⁻⁴Jです。

ラブの軌道エネルギーは、8.665×10⁻²⁴Jmです。

光子の公転軌道エネルギーは、1.233×10⁻⁴¹Jmです。

光子の自転軌道エネルギーは、6.112×10⁻⁵⁷Jmです。

1電子のラブが1秒間に作る、熱と成る電気の光子のエネルギーは、

1.233×10⁻⁴¹Jm÷（2.066×10⁻⁵ｍ）×6.336×10¹⁵公転×7.378×10⁵＝3.781×10⁻²¹J×7.378×10⁵＝7.378×10⁵℃です。

1電子のラブが1秒間に作る、引力と成る磁気の光子のエネルギーは、

1.233×10⁻⁴¹Jm÷｛2.066×10⁻⁵ｍ÷(7.378×10⁵)｝×6.336×10¹⁵公転＝2.790×10⁻¹⁵J、です。

これを表にします。

２．　ブラックホールの温度は10⁻⁷℃であると考えられている理由について。（2007年4月18日に提出した、特願2007−133476．の「請求項7」）

私は、ブラックホールの温度は、�B太陽の質量をブラックホールにすると、半径３Kmになる。場合、温度は5.444×10¹¹℃であると考えます。

しかし、ブラックホールの温度は10⁻⁷℃であると考えられている。

この理由について。

ブラックホールの電子のラブの公転軌道は、1.434×10⁻¹⁶ｍです。

温度になるためには光子の軌道は遠赤外線である10⁻⁵ｍでなければいけません。

太陽の外側は、6×10³℃ですから、電子のラブの公転軌道は、

1.058×10⁻¹⁰ｍ÷（6×10³）^1/2=1.058×10⁻¹⁰ｍ÷77.46=1.366×10⁻¹²ｍです。

これが、可視光として届きますから、約7×10⁻⁷ｍから3×10⁻⁷ｍとして届きます。

太陽を10⁻⁸ｍで出発するとしますと、出発するまでに、光子は、1.366×10⁻¹²ｍから10⁻⁸ｍまで伸びています。約10⁴倍に伸びました。

ブラックホールでは、10^−16＋4＝10⁻¹²ｍで出発するとしますと、これは可視光にも温度にもなりません。温度に成る遠赤外線までなるには、光子の軌道は10⁻⁵÷10⁻¹²＝10⁷倍に伸びなければいけません。それで、ブラックホールの温度は10⁻⁷℃であると考えられている。

３．　星の質量が太陽の質量のK倍である場合、星の中央部の電子のラブの公転軌道はいくらか。（2007年4月18日に提出した、特願2007−133476．の「請求項20」）

太陽の質量のK倍である星の中央部の温度は、

太陽の中央部の温度×K²＝15×10⁶×K²　です。

それで、A=（15×10⁶×K²）^1/2=3.873×10³×K

公転軌道＝1.058×10⁻¹⁰ｍ÷（3.873×10³×K）＝2.732×10⁻¹⁴ｍ÷K

2.732×10⁻¹⁴ｍは、太陽の中央部の電子のラブの公転軌道です。

星の質量が太陽の質量のK倍である場合、星の中央部の電子のラブの公転軌道は、2.732×10⁻¹⁴ｍ÷K　です。

・例えば、星の中央部の電子のラブの公転軌道が10⁻¹⁵ｍである場合、この星の質量は太陽の何倍か。

K倍とする。

公転軌道＝2.732×10⁻¹⁴ｍ÷K

10⁻¹⁵ｍ＝2.732×10⁻¹⁴ｍ÷K

K=2.732×10⁻¹⁴ｍ÷10⁻¹⁵ｍ＝27.32

星の中央部の電子のラブの公転軌道が10⁻¹⁵ｍである場合、この星の質量は太陽の27.32倍です。

公転軌道が10⁻¹⁵ｍである場は、太陽の質量の27.32倍の星が存在する場です。

・例えば、公転軌道が、5×10⁻¹⁵ｍである場は、太陽の何倍の質量の星が存在するか。

5×10⁻¹⁵ｍ＝2.732×10⁻¹⁴ｍ÷K

K=2.732×10⁻¹⁴ｍ÷（5×10⁻¹⁵ｍ）＝5.464

公転軌道が5×10⁻¹⁵ｍである場は、太陽の質量の5.464倍の星が存在する場です。

・例えば、公転軌道が、10⁻¹⁶ｍである場は、太陽の何倍の質量の星が存在するか。

10⁻¹⁶ｍ＝2.732×10⁻¹⁴ｍ÷K

K=2.732×10⁻¹⁴ｍ÷10⁻¹⁶ｍ＝273.2

公転軌道が10⁻¹⁶ｍである場は、太陽の質量の273.2倍の星が存在する場です。

しかし、ここはブラックホールの場なので、太陽の質量の273.2倍の星は存在しない。

４．　ブラックホールは、太陽の質量の30倍の星が爆発した後に残る、高エネルギーの中央部が収縮したものです。どれ位収縮するのか。（2007年4月18日に提出した、特願2007−133476．の「請求項21」）

太陽の質量の30倍の星の中央部の公転軌道は、

2.732×10⁻¹⁴ｍ÷30＝9.11×10⁻¹⁶ｍです。

これが収縮して、ブラックホールの電子のラブの公転軌道は、1.434×10⁻¹⁶ｍになる。これは太陽の質量をブラックホールにすると、半径3Kmになる場合の電子のラブの公転軌道です。

9.11×10⁻¹⁶ｍ÷（1.434×10⁻¹⁶ｍ）＝6.353分の1に収縮するとブラックホールになる。

1.434×10⁻¹⁶ｍ÷（9.11×10⁻¹⁶ｍ）＝0.157倍に収縮するとブラックホールになる。

ブラックホールは、太陽の質量の30倍の星が爆発した後に残る、高エネルギーの中央部が収縮したものです。このブラックホールを考えた時、収縮する割合を、10^1/2=3.162としました。それで、公転軌道は、2.88×10⁻¹⁶ｍに成りました。

ここでは、6.353分の1に収縮するとして計算します。

この星のA＝3.873×10³×30＝1.162×10⁵です。

公転軌道は、1.058×10⁻¹⁰ｍ÷（1.162×10⁵）＝9.105×10⁻¹⁶ｍです。

それが、6.353分の1に収縮すると、9.105×10⁻¹⁶ｍ÷6.353＝1.433×10⁻¹⁶ｍです。

・この事によって、「請求項6」で考えた�@と�Aは同じである事が理解できた。

５．　どうしてブラックホールにダークマターである自転している電子のラブと陽子のラブは引き付けられるか。（2007年5月10日に提出した、特願2007−150959．の「請求項13」）

・ブラックホールの電子のラブと陽子のラブが自転して作る磁気の光子のエネルギーは、ダークマターである自転する電子のラブと陽子のラブが作る磁気の光子のエネルギーの何倍か。

エネルギーは軌道に反比例しますから、

10⁻⁹m÷10⁻¹⁶ｍ＝10⁷倍です。

それで、ブラックホールにダークマターである自転している電子のラブと陽子のラブは引き付けられる。

ダークマターの自転軌道は、10⁻⁹⁻⁸ｍ＝10⁻¹⁷ｍ、です。

ブラックホールの公転軌道は、10⁻¹⁶ｍです。

同じ軌道なので引き付けられる。

ダークマターの電子のラブが1秒間に作る引力となる磁気の光子のエネルギーはいくらか。

ダークマターは、−273℃ですから、A=−273^1/2=−16.523、です。

ダークマターの電子のラブが1秒間に作る引力となる磁気の光子のエネルギー＝1.233×10⁻⁴¹Jm÷(2.066×10⁻⁵ｍ÷A)×6.336×10¹⁵公転＝1.233×10⁻⁴¹Jm÷(2.066×10⁻⁵ｍ×16.523)×6.336×10¹⁵公転＝2.289×10⁻²²J、です。

ブラックホールの電子のラブが1秒間に作る引力となる磁気の光子のエネルギーは、2.790×10⁻¹⁵Jです。

それで、ブラックホールが作る引力は、ダークマターが作る引力の、2.790×10⁻¹⁵J÷(2.289×10⁻²²J)＝1.219×10⁷倍です。

それで、ダークマターはブラックホールに引き付けられる。

６．　ブラックホールの電子のラブと陽子のラブは自転し公転している。（2007年6月15日に提出した、特願2007−183718．の「請求項8」）

私は、ブラックホールの場では、電子のラブと陽子のラブは、公転せず自転だけすると考えてきました。ところが、今回、ダークマターの活性化を考えますと、ブラックホールの電子のラブは公転していて、公転してできる電気の光子が、ダークマターである自転する電子のラブに付加することを理解しました。この理解により、ブラックホールの電子のラブは公転する事を知りました。

ブラックホールの電子のラブと陽子のラブは自転し公転する。

７．　水素や元素が存在しない軌道の速度はどれくらいか。速度が2×10⁵Kmと成るのは周囲何Kmの軌道か。ブラックホールを10ⁿ太陽質量とする。その軌道の引力はいくらか。(2009年5月11日に提出した、特願2009−114091．の｢請求項29｣)

・水素や元素が存在しない軌道の速度はどれくらいか。

第1世代の星のブラックホールが作った速度が、2.750×10⁵Km(現在金星の軌道)、2.339×10⁵Km(現在地球の軌道)、1.895×10⁵Km(現在火星の軌道)、には、第1世代の惑星は存在しなかった。惑星を作る水素が存在しなかったからです。

中性子星が作った速度が8.583×10⁴Kmの軌道に水星ができ、これ以上の速度の軌道には惑星ができなかった。惑星に成る元素が存在しなかったからです。

それで、軌道の速度が約2×10⁵Km以上の軌道には、水素や元素が存在しない。

水素や元素が存在しない軌道の速度は約2×10⁵Km以上です。

・速度が2×10⁵Kmと成るのは周囲何Kmの軌道か。ブラックホールを10ⁿ太陽質量とする。

速度² ＝(2×10⁵Km)²＝5.4×10^18＋2×n/3JKm÷距離

距離＝5.4×10^18＋2×n/3÷(2×10⁵Km)²＝5.4÷4×10⁸Km×10^2×n/3＝1.35×10⁸×10^2×n/3Km

速度が2×10⁵Kmと成るのは周囲1.35×10⁸×10^2×n/3Kmの軌道です。

それでは、ブラックホールの質量と、速度が2×10⁵Kmになる軌道の距離を算出する。

ブラックホールが10⁹太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×9/3Km＝1.35×10^8＋6Km=1.35×10¹⁴Km

ブラックホールが10⁸太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×8/3Km＝1.35×10⁸×10^5.3333Km=1.35×10¹³×2.155Km＝2.909×10¹³Km

ブラックホールが10⁷太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×7/3Km＝1.35×10⁸×10^4.6667Km=1.35×10¹²×4.642Km＝6.267×10¹²Km

ブラックホールが10⁶太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×6/3Km＝1.35×10^8＋4Km=1.35×10¹²Km

ブラックホールが10⁵太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×5/3Km＝1.35×10^8×10^3.3333Km=1.35×10¹¹×2.155Km＝2.909×10¹¹Km

ブラックホールが10⁴太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×4/3Km＝1.35×10⁸×10^2.6667Km=1.35×10¹⁰×4.642Km＝6.267×10¹⁰Km

ブラックホールが10³太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×3/3Km＝1.35×10^8＋2Km=1.35×10¹⁰Km

ブラックホールが10²太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×2/3Km＝1.35×10⁸×10^1.3333Km=1.35×10⁹×2.155Km＝2.909×10⁹Km

ブラックホールが10太陽質量の場合。

距離＝1.35×10⁸×10^2×n/3Km＝1.35×10⁸×10^2×1/3Km＝1.35×10⁸×10^0.6667Km=1.35×10⁸×4.642Km＝6.267×10⁸Km

・速度が2×10⁵Kmの軌道の引力はいくらか。

引力＝速度⁴＝(2×10⁵Km)⁴＝16×10²⁰(J)

速度が2×10⁵Kmの軌道の引力は16×10²⁰Jです。

この事によって理解できる事。

1. 軌道の速度が約2×10⁵Km以上の軌道には、水素や元素が存在しない。

水素や元素が存在しない軌道の速度は約2×10⁵Km以上です。

2. 速度が2×10⁵Kmと成るのは周囲1.35×10⁸×10^2×n/3Kmの軌道です。(ブラックホールを10ⁿ太陽質量とする。)

3. 速度が2×10⁵Kmの軌道の引力は16×10²⁰Jです。

4. 軌道引力が16×10²⁰J以上の軌道では、物質は存在しない。

5. 軌道引力が16×10²⁰J以上の軌道の物質は、ブラックホールに引かれて、ブラックホールの周囲に存在する。

6. ブラックホールの軌道の引力が星を作った。

８．　速度が光速と成るのは周囲何Kmの軌道か。この軌道の引力はいくらか。ブラックホールを10ⁿ太陽質量とする。(2009年5月11日に提出した、特願2009−114091．の｢請求項29｣)

速度² ＝(3×10⁵Km)²＝5.4×10^18＋2×n/3JKm÷距離

距離＝5.4×10^18＋2×n/3÷(3×10⁵Km)²＝6×10⁷Km×10^2×n/3＝6×10⁷×10^2×n/3Km

速度が光速と成るのは周囲6×10⁷×10^2×n/3Kmの軌道です。

・ブラックホールと6×10⁷×10^2×n/3Kmの軌道の引力はいくらか。

軌道エネルギー＝5.4×10^18＋2×n/3JKm÷距離＝5.4×10^18＋2×n/3JKm÷(6×10⁷×10^2×n/3Km)＝9×10¹⁰J

引力＝軌道エネルギー²＝(9×10¹⁰J)²＝81×10²⁰J＝定数

速度が光速になる軌道の引力は81×10²⁰Jで、一定値です。

どのような質量のブラックホールでも、引力が81×10²⁰Jの軌道の物質はブラックホールに引かれて、その軌道には何も存在しない。

光速になる半径は、6×10⁷×10^2×n/3Kmです。

前の｢請求項２９｣で理解したように、軌道の速度が2×10⁵Km以上の軌道では、物質はブラックホールに引かれて存在しない。

これを、“ブラックホールの引力の法則”と名づけます。

即ち、“ブラックホールの引力の法則”とは、「軌道の速度が2×10⁵Km以上の軌道では、物質はブラックホールに引かれて存在しない。ブラックホールの質量が10ⁿ太陽質量のとき、半径1.35×10⁸×10^2×n/3Kmまでの物質は、16×10²⁰Jの引力に引かれて、何も存在しない。」ということです。

勿論、光速の軌道も、この中に含まれます。

光速の軌道は、半径6×10⁷×10^2×n/3Kmですから、

6×10⁷×10^2×n/3Km÷(1.35×10⁸×10^2×n/3Km)＝0.4444(倍)の距離です。

光速の場合、中心から6×10⁷Km×10^2×n/3の軌道まで、何も存在しない。この軌道の物質はブラックホールに引かれるので、何も存在しない。

ブラックホールの質量と、速度が光速になる軌道の距離を算出する。

ブラックホールが10⁹太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×9/3Km＝6×10^7＋6Km=6×10¹³Km

ブラックホールが10⁸太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×8/3Km＝6×10⁷×10^5.3333Km=6×10¹²×2.155Km＝1.293×10¹³Km

ブラックホールが10⁷太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×7/3Km＝6×10⁷×10^4.6667Km=6×10¹¹×4.642Km＝2.785×10¹²Km

ブラックホールが10⁶太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×6/3Km＝6×10^7＋4Km=6×10¹¹Km

ブラックホールが10⁵太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×5/3Km＝6×10⁷×10^3.3333Km=6×10¹⁰×2.155Km＝1.293×10¹¹Km

ブラックホールが10⁴太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×4/3Km＝6×10⁷×10^2.6667Km=6×10⁹×4.642Km＝2.785×10¹⁰Km

ブラックホールが10³太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×3/3Km＝6×10^7＋2Km=6×10⁹Km

ブラックホールが10²太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×2/3Km＝6×10⁷×10^1.3333Km=6×10⁸×2.155Km＝1.293×10⁹Km

ブラックホールが10太陽質量の場合。

距離＝6×10⁷×10^2×n/3Km＝6×10⁷×10^2×1/3Km＝6×10⁷×10^0.6667Km=6×10⁷×4.642Km＝2.785×10⁸Km

これを表に示す。

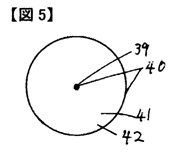
この事より理解できること。

1. 光速になる距離は、6×10⁷×10^2×n/3Km、です。

2. 光速になる軌道の引力は、81×10²⁰Jです。

3. 半径6×10⁷×10^2×n/3Kmで、引力が81×10²⁰Jである、光速の軌道では、物質はブラックホールに引かれ、何も存在しない。

4. “ブラックホールの引力の法則”とは、「軌道の速度が2×10⁵Km以上の軌道では、物質はブラックホールに引かれて存在しない。質量が10ⁿ太陽質量のブラックホールの場合、半径1.35×10⁸×10^2×n/3Kmまでの物質は、16×10²⁰Jの引力に引かれて、何も存在しない。」ということです。

勿論、光速の軌道も、この中に含まれます。

5. 光速の軌道は、速度が2×10⁵Kmの軌道の0.4444倍の距離です。

９．　シュバルツシルト半径の場では、どうして光子がのみ込まれるのか。

シュバルツシルト半径は数百万Kmです。ブラックホールを10⁶太陽質量とする。

・シュバルツシルト半径の軌道の速度はいくらか。シュバルツシルト半径を10⁶Kmとする。

速度²＝5.4×10^18＋2n/3JKm÷10⁶Km＝5.4×10^18＋2×6/3JKm÷10⁶Km＝5.4×10¹⁶J

速度＝(5.4×10¹⁶)^1/2=2.3×10⁸Km

シュバルツシルト半径の軌道の速度は2.3×10⁸Kmで、光速3×10⁵Kmより速い場である。

それで、光子はのみ込まれる。

【図面の簡単な説明】

【図5】｢ブラックホールの引力の法則｣を示す。

ブラックホールの周囲の軌道の速度が2×10⁵Km以上の場合、周囲には何も存在しない。その周囲の物質はブラックホールに引かれるためです。“ブラックホールの引力の法則”とは、「ブラックホールの周囲の軌道の速度が2×10⁵Km以上の場合、周囲には何も存在しない。ブラックホールの質量が10ⁿ太陽質量のとき、ブラックホールから、半径3.15×10⁸Km×10^2×n/3までの物質は、16×10²⁰Jの引力に引かれるので、この空間には何も存在しない。」事です。

【符号の説明】

３９　質量が10ⁿ太陽質量のブラックホール

４０　軌道の速度が2×10⁵Kmである軌道は、半径3.15×10⁸×10^2n/3Kmです。

４１　この軌道の引力は16×10²⁰Jです。

４２　何も存在しない空間