2012年3月の日本天文学会での講演　ａ
タイトル「宇宙の中心のブラックホールの質量とダークマター数」

 

　宇宙の公転軌道エネルギーの式はどのようであるか。一般式を求める。宇宙の公転軌道エネルギー＝公転速度²×中心からの距離。宇宙の公転軌道は1周するのに何年かかるか。現在まで何周しているか。一般式を求める。
1周するのにかかる年数＝円周÷1年間に走る距離＝2×3.14×半径(光年)×9.46×10¹²Km÷(秒速×365×24×60×60)＝1.883×半径(光年)÷秒速×10⁶。何周しているか＝137×10⁸年÷1周するのにかかる年数＝137×10⁸年÷(1.883×半径(光年)÷秒速×10⁶)＝7.276×10³×秒速÷半径(光年)。グレートウォールが半径3×10^７光年の軌道で、現在までに、1公転していると仮定する。宇宙の公転軌道エネルギー＝公転速度²×中心からの距離＝公転速度²×3×10^７×9.46×10¹²Km＝公転速度²×2.838×10²⁰JKm。１周しているから＝7.276×10³×秒速÷半径(光年)＝7.276×10³×秒速÷(3×10⁷)＝2.425×10⁻⁴×秒速＝１(周)。秒速＝1÷(2.425×10⁻⁴)＝4.124×10³(Km)。この宇宙の公転軌道エネルギーは、(4.124×10³)²×2.838×10²⁰JKm÷距離＝4.827×10²⁷JKm÷距離、です。この宇宙の公転軌道エネルギー＝10⁻²⁵J×ブラックホールの表面の原子数×10⁵Km÷距離＝4.827×10²⁷JKm÷距離。ブラックホールの表面の原子数＝4.827×10²⁷JKm÷10^-20JKm=4.827×10⁴⁷(個)。表面の原子数＝4πｒ²＝4.827×10⁴⁷。ブラックホールの原子数＝4π/3×ｒ³＝4π/3×(1.960×10²³)³＝3.152×10⁷⁰(個)。ブラックホールの原子数÷(太陽の原子数)＝3.152×10⁷⁰個÷(1.198×10⁵⁷個)＝2.631×10¹³(太陽質量)。　ブラックホールを作るために必要な質量(全体の質量)＝9.458×10⁵×2.631×10¹³太陽質量＝2.488×10¹⁹太陽質量。全体の原子数＝2.488×10¹⁹太陽質量×太陽の原子数＝2.488×10¹⁹×1.198×10⁵⁷個＝2.981×10⁷⁶個。ダークマターの数＝ビッグバンの以前の原子数÷全体の原子数＝1.0765×10⁷⁹個÷（2.981×10⁷⁶個）＝3.611×10²（倍）。

説明
１． グレートウォールが半径3×10^７光年の軌道で、現在までに、1公転している事により、宇宙の軌道エネルギーを求めます。

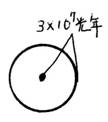
・宇宙の公転軌道エネルギー＝公転速度²×中心からの距離＝公転速度²×3×10^７×9.46×10¹²Km＝公転速度²×2.838×10²⁰JKm。

１周している事から＝公転した距離÷円周＝­秒速(Km)×137億年の秒数÷円周＝秒速(Km)×137×10⁸×365×24×60×60÷(2×3.14×3×10⁷×3×10⁵Km×365×24×60×60)＝2.424×10⁻⁴＝１(周)
秒速＝1÷(2.424×10⁻⁴)＝4.124×10³(Km)

○この宇宙の公転軌道エネルギーは、(4.124×10³)²×2.838×10²⁰JKm÷距離＝4.827×10²⁷JKm÷距離、です。
２． 軌道エネルギーは、表面から出発する電気の光子1個のエネルギー×中心となる物の表面の原子数×10⁵Km÷距離、です。10⁵Kmは見かけ上に換算する定数です。(これは「宇宙の軌道エネルギー」に記した。)

宇宙の軌道エネルギー＝中心のブラックホールが作る軌道エネルギー＝ブラックホールから出発する電気の光子1個のエネルギー×ブラックホールの表面の原子数×10⁵Km÷距離＝10⁻²⁵J×ブラックホールの表面の原子数×10⁵Km÷距離＝4.827×10²⁷JKm÷距離
ブラックホールの表面の原子数＝4.827×10²⁷JKm÷(10⁻²⁵J×10⁵Km)＝4.827×10⁴⁷(個)
半径にr個の原子が存在するとする。
ブラックホールの表面の原子数＝4πr²=4.827×10⁴⁷(個)
r²＝4.827×10⁴⁷÷4π＝3.843×10⁴⁶(個)
r＝1.960×10²³(個)
中心のブラックホールの原子数＝4π/3×r³＝4π/3×(1.960×10²³)³＝3.152×10⁷⁰(個)
中心のブラックホールの原子数÷太陽の原子数＝3.152×10⁷⁰個÷(1.198×10⁵⁷個)＝2.631×10¹³(太陽質量)
○宇宙の中心のブラックホールの質量は、2.631×10¹³太陽質量です。原子数は3.152×10⁷⁰個です。
３．ブラックホールを作るために必要な全体の原子数を計算する。
この中心のブラックホールを作るために必要な全体の質量＝9.458×10⁵×中心のブラックホールの太陽質量＝9.458×10⁵×2.631×10¹³太陽質量＝2.488×10¹⁹太陽質量
全体の原子数＝2.488×10¹⁹太陽質量×太陽の原子数＝2.488×10¹⁹×1.198×10⁵⁷個＝2.981×10⁷⁶個
○中央のブラックホールを作るために必要な全体の質量は2.488×10¹⁹太陽質量で、原子数
は2.981×10⁷⁶個です。
表に示します。

	原子数	太陽質量
中心のブラックホールの原子数	3.152×1070(個)	2.631×1013太陽質量
この中心のブラックホールを作るために必要な全体の原子数	2.981×1076個	2.488×1019太陽質量
ビッグバンの以前の陽子の数と電子の数	1.077×1079個

○ビッグバンの以前の陽子の数と電子の数は1.077×10⁷⁹個である。(これは、「ビッグバンの以前の大きさと原子数と引力」で説明した)
４． ビッグバンの以前に存在した陽子数と全体の原子数を比較する。
ビッグバンの以前の陽子の数÷全体の原子数＝1.077×10⁷⁹個÷(2.981×10⁷⁶個)＝361(倍)
ダークマターとは、自転だけしている電子のラブと、自転だけしている陽子のラブです。(この事については、｢ダークマターとは何か｣で説明した)
○それで、ビッグバンの以前、原子に成れなかった自転だけしている電子のラブと、自転だけしている陽子のラブは原子に成ったものの361倍です。
５． どうして原子数は361分の1だけよりできなかったのか、その理由を説明する。
それは、ビッグバンの以前、中央に陽子のラブの集団が有り、その集団が軌道を作っていた。
電子のラブはその軌道上を回転していた。
それは、まるで、太陽は惑星の軌道を作っているように、陽子の集団は電子が走る軌道を作っていた。
陽子の集団が作る軌道は360個の平面でできているとする。電子の軌道はその平面の１つです。360分の1の平面にしか電子は存在しません。
○それで、陽子がビッグバンで球状に放出したとき、上に走った陽子や、下に走った陽子や。斜めに走った陽子はそこに電子が居ないので、原子に成れません。原子に成れず、そのまま自転し続けました。これがダークマターです。
それで、陽子が電子と衝突し、原子に成ったものは360分の1です。

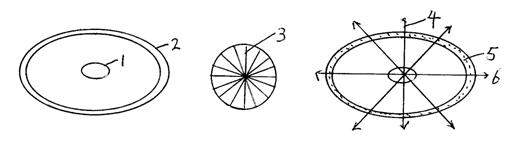
図の説明
１は、ビッグバンの以前の、陽子のラブの集団で球体。平面上に電子のラブの軌道を作っている。
２は、ビッグバンの以前の、電子のラブの軌道
３は、陽子のラブの集団が作る軌道は360個の平面でできているとする。

４は、陽子のラブがビッグバンで球状に放出する。上下の方向、斜めの方向に走った陽子のラブは、そこに電子のラブが存在しないので、そのまま自転し続ける。これがダークマターです。
５は、平面の軌道上の電子のラブ
６は、電子のラブの軌道の方向に走った陽子のラブ。この陽子のラブだけが電子のラブと衝突し、原子に成る事ができた。