「宇宙の形2」 (この考えは、2013年2月16日に提出した、特願2013−028476に記した)
1. 各々の時代の宇宙の速度はいくらか。
半径=4.827×1027JKm÷速度2
速度2=4.827×1027JKm÷半径
10−20m時代で、半径5×103光年の場合。
速度2=4.827×1027JKm÷(5×103×9.46×1012Km)=1.021×1011J
速度=(1.021×1011)1/2=3.195×105Km
10−19m時代で、半径5×104光年の場合。
速度2=4.827×1027JKm÷(5×104×9.46×1012Km)=1.021×1010J
速度=(1.021×1010)1/2=1.010×105Km
10−18m時代で、半径5×105光年の場合。
速度2=4.827×1027JKm÷(5×105×9.46×1012Km)=1.021×109J
速度=(1.021×109)1/2=3.195×104Km
10−17m時代で、半径5×106光年の場合。
速度2=4.827×1027JKm÷(5×106×9.46×1012Km)=1.021×108J
速度=(1.021×108)1/2=1.010×104Km
10−16m時代で、半径1.25×107光年の場合。
速度2=4.827×1027JKm÷(1.25×107×9.46×1012Km)=4.082×107J
速度=(4.082×107)1/2=6.389×103Km
10−16m時代で、半径2.5×107光年の場合。
速度2=4.827×1027JKm÷(2.5×107×9.46×1012Km)=2.041×107J
速度=(2.041×107)1/2=4.518×103Km
10−16m時代で、半径5×107光年の場合。
速度2=4.827×1027JKm÷(5×107×9.46×1012Km)=1.021×107J
速度=(1.021×107)1/2=3.195×103Km
10−15m時代で、半径1.25×108光年の場合。
速度2=4.827×1027JKm÷(1.25×108×9.46×1012Km)=4.082×106J
速度=(4.082×106)1/2=2.020×103Km
10−15m時代で、半径2.5×108光年の場合。
速度2=4.827×1027JKm÷(2.5×108×9.46×1012Km)=2.041×106J
速度=(2.041×106)1/2=1.429×103Km
10−15m時代で、半径5×108光年の場合。
速度2=4.827×1027JKm÷(5×108×9.46×1012Km)=1.021×106J
速度=(1.021×106)1/2=1.010×103Km
10−14m時代で、半径1.25×109光年の場合。
速度2=4.827×1027JKm÷(1.25×109×9.46×1012Km)=4.082×105J
速度=(4.082×105)1/2=6.389×102Km
10−14m時代で、半径2.5×109光年の場合。
速度2=4.827×1027JKm÷(2.5×109×9.46×1012Km)=2.041×105J
速度=(2.041×105)1/2=4.518×102Km
10−14m時代で、半径5×109光年の場合。
速度2=4.827×1027JKm÷(5×109×9.46×1012Km)=1.021×105J
速度=(1.021×105)1/2=3.195×102Km
2. 各時代の外側の軌道は何回転したか。
回転数=回転した距離÷円周=回転した秒数×秒速÷(2π×軌道半径)
10−14m時代で半径5×109光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=137×108年×365×24×60×60秒×3.195×102Km/秒÷(2π×5×109×9.46×1012Km)=137×108×3.154×107秒×3.195×102Km/秒÷(2π×5×109×9.46×1012Km)=1.379×1020Km÷(2.970×1023Km)=4.643×10−4回
10−15m時代で半径5×108光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=109年×3.154×107秒×1.010×103Km/秒÷(2π×5×108×9.46×1012Km)=3.186×1019Km÷(2.970×1022Km)=1.073×10−3回
10−16m時代で半径5×107光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=108年×3.154×107秒×3.195×103Km/秒÷(2π×5×107×9.46×1012Km)=1.008×1019Km÷(2.970×1021Km)=3.394×10−3回
10−17m時代で半径5×106光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=107年×3.154×107秒×1.010×104Km/秒÷(2π×5×106×9.46×1012Km)=3.186×1018Km÷(2.970×1020Km)=1.073×10−2回
10−18m時代で半径5×105光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=106年×3.154×107秒×3.195×104Km/秒÷(2π×5×105×9.46×1012Km)=1.008×1018Km÷(2.970×1019Km)=3.394×10−2回
10−19m時代で半径5×104光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=105年×3.154×107秒×1.010×105Km/秒÷(2π×5×104×9.46×1012Km)=3.186×1017Km÷(2.970×1018Km)=1.073×10−1回
10−20m時代で半径5×103光年の回転数。
回転した秒数×秒速÷(2π×軌道半径)=104年×3.154×107秒×3.195×105Km/秒÷(2π×5×103×9.46×1012Km)=1.008×1017Km÷(2.970×1017Km)=3.394×10−1回
まとめて表に示す。
表1
|
時代 |
軌道半径 |
速度 |
年数 |
回転数 |
|
10−20m |
5×103光年 |
3.915×105Km |
104年 |
3.394×10−1回 |
|
10−19m |
5×104光年 |
1.010×105Km |
105年 |
1.073×10−1回 |
|
10−18m |
5×105光年 |
3.915×104Km |
106年 |
3.394×10−2回 |
|
10−17m |
5×106光年 |
1.010×104Km |
107年 |
1.073×10−2回 |
|
10−16m |
1.25×107光年 |
6.389×103Km |
|
|
|
10−16m |
2.5×107光年 |
4.518×103Km |
|
|
|
10−16m |
5×107光年 |
3.915×103Km |
108年 |
3.394×10−3回 |
|
10−15m |
1.25×108光年 |
2.020×103Km |
|
|
|
10−15m |
2.5×108光年 |
1.429×103Km |
|
|
|
10−15m |
5×108光年 |
1.010×103Km |
109年 |
1.073×10−3回 |
|
10−14m |
1.25×109光年 |
6.389×102Km |
|
|
|
10−14m |
2.5×109光年 |
4.518×102Km |
|
|
|
10−14m |
5×109光年 |
3.195×102Km |
1.37×1010年 |
4.643×10−4回 |
3. 回転数が少ないことによって何が解るか。
回転数が少ないことによって、宇宙は扁平になっていないことが理解できる。
4. 宇宙の形はどのようであるか。
宇宙の中心のブラックホールが回転しながらまっすぐ進んだ場合、宇宙の球体は膨張しながら進む。
進む距離は進む時間に比例するとする。
特願2013−027190の「請求項13」のように考える。
時間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010年:109年:108年:107年:106年:105年:104年
それで、1010年を10cmとしますと、10 cm:1 cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
空間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010光年:109光年:108光年:107光年106光年:105光年:104光年、です。
それで、1010光年を10 cmとしますと、10 cm:1cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
中心のブラックホールが進んだ距離を直線とする。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙をまとめて示す。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙ができる。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙は、0.05555mm進み直径0.1111mmの宇宙になる。
10―16m時代の宇宙ができる。
それから、10―16m時代の宇宙は0.51mm進み、直径1mmの宇宙になる。
10―15m時代の宇宙ができる。
それから、10−15m時代の宇宙は、0.5cm進み、直径1cmの宇宙になる。
1014m時代の宇宙ができる。
まず1.25×109光年の宇宙ができる。
1.25cm進んで、半径1.25cmの宇宙ができる。
2.5×109光年の宇宙ができる。
それから、2.5cm進み、半径2.5cmの宇宙ができる。
5×109光年の宇宙ができる。
それから、5cm進み、半径5cmの宇宙ができる。
これを図示する。
これは、1010光年:10cm=1010×9.46×1012×103×102:10=9.46×1026:1、の縮図です。
【図面の簡単な説明】
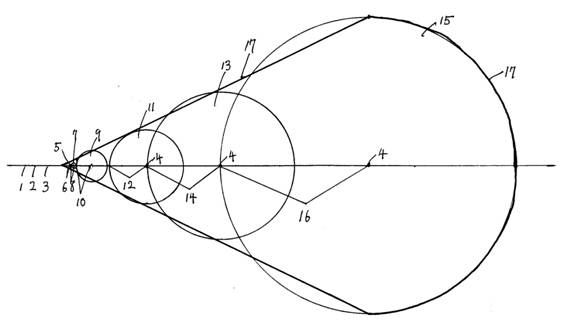
【図1】図1は宇宙の側面図ただし、宇宙が出来ていく状態をしめす。
時間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010年:109年:108年:107年:106年:105年:104年
それで、1010年を10cmとしますと、10 cm:1 cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
空間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010光年:109光年:108光年:107光年:106光年:105光年:104光年、です。
それで、1010光年を10 cmとしますと、10 cm:1cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
中心のブラックホールが進んだ距離を直線とする。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙をまとめて示す。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙ができる。
10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙は、0.05555mm進み、直径0.1111mmの宇宙になる。
10―16m時代の宇宙ができる。
それから、10―16m時代の宇宙は、0.5mm進み、直径1mmの宇宙になる。
10―15m時代の宇宙ができる。
それから、10−15m時代の宇宙は、0.5cm進み、直径1cmの宇宙になる。
10−14m時代の宇宙ができる。
まず1.25×109光年の宇宙ができる。
1.25cm進んで、半径1.25cmの宇宙ができる。
2.5×109光年の宇宙ができる。
それから、2.5cm進み、半径2.5cmの宇宙ができる。
5×109光年の宇宙ができる。
それから、5cm進み、半径5cmの宇宙ができる。
これは、1010光年:10cm=1010×9.46×1012×103×102:10=9.46×1026:1、の縮図です。
【符号の説明】
1 時間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010年:109年:108年:107年:106年:105年:104年
それで、1010年を10cmとしますと、10 cm:1 cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
2 空間の比は、10−14m時代:10−15m時代:10―16m時代:10−17m時代:10−18m時代:10−19m時代:10−20m時代=1010光年:109光年:108光年:107光年:106光年:105光年:104光年、です。
それで、1010光年を10 cmとしますと、10 cm:1cm:1mm:10−1 mm:10−2 mm:10−3 mm:10−4 mm、です。
3 宇宙の中心のブラックホールが進んだ距離を直線とする。
4 宇宙の中心のブラックホール
5 10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙
6 10−17m時代の宇宙、10−18m時代の宇宙、10−19m時代の宇宙、10−20m時代の宇宙は、0.05555mm進み直径0.1111mmの宇宙になる。
7 10―16m時代の宇宙
8 10―16m時代の宇宙は、0.5mm進み、直径1mmの宇宙になる。
9 10−15m時代の宇宙
10 10−15m時代の宇宙は、0.5cm進み、直径1cmの宇宙になる。
11 半径1.25×109光年の宇宙
12 1.25cm進んで、半径1.25cmの宇宙ができる。
13 半径2.5×109光年の宇宙
14 2.5cm進み、半径2.5cmの宇宙ができる。
15 半径5×109光年の宇宙
16 5センチ進み、半径5センチの宇宙ができる。
17 宇宙が進んでできた形
この図は、1010光年:10cm=1010×9.46×1012×103×102:10=9.46×1026:1、の縮図です。
図面
【図1】
【特許文献1】特願2013−027190