「宇宙とダークマター」 (この考えは、2012年12月27日に提出した、特願2012−286352に記した)
1. ダークマターが宇宙の回転速度を作る原理は何か。
宇宙の回転速度は中心のブラックホールによってできると考えてきた。
しかし、アンドロメダ銀河の回転速度はどこまでも同じ回転速度です。
この事は、回転速度は中心のブラックホールによってできるだけではなく他の何かによってもできることを示す。
私は、宇宙の回転速度は軌道のエネルギーが速度2になっていると考える。
回転速度を作っているのは、軌道のエネルギーであり、軌道の電気の光子のエネルギーである。
回転速度を作っているのは、ブラックホールが作る軌道のエネルギーであり、更にその他のものが電気の光子を作っている。
それはダークマターである。ダークマターがどうして電気の光子を作っているのか。
それは、電子のラブが自転しながら公転することにより、磁気の光子と電気の光子を作ることと同じです。
電子のラブは自転しながら公転することによって、磁気の光子と電気の光子を作る。
電子のラブは自転し、磁気の光子を作り、公転し、電気の光子を作る。
電子のラブに成れなかったダークマターの実態は自転だけしている電子のラブである。
陽子のラブに成れなかったダークマターの実態は自転だけしている陽子のラブである。
それで、公転の代わりに回転すると、そこに生まれるのは、電気の光子です。
ダークマターはブラックホールが作る回転軌道を走る。
ダークマターは自転しながら走るので、電気の光子を作る。
ダークマターが作る電気の光子が軌道のエネルギーになり、回転速度2を作る。
これが、ダークマターが回転速度を作る原理です。
2. 宇宙の球体の軌道エネルギーはどのような式であるか。
宇宙のエネルギーの95.7%はダークマターのエネルギーであるから、宇宙の軌道のエネルギーはダークマターのエネルギーです。
私は、宇宙の球体の軌道のエネルギーを次のように考えていた。
宇宙の球体の軌道のエネルギー=軌道のダークマターの数×1個のダークマターが7.96×107自転で作る光子のエネルギー=軌道のダークマターの数×(8.857×10−41J×7.96×107自転)=軌道のダークマターの数×7.050×10−33J、と考えてきた。
しかし、このエネルギーは磁気の光子のエネルギーであり、電気の光子のエネルギーではない。
宇宙の球体の軌道エネルギーはダークマターが中心のブラックホールが作った軌道を回転することによってできる。
宇宙の球体の軌道エネルギー=軌道のダークマターの数×1個のダークマターのエネルギー
宇宙の球体の軌道エネルギーの式は、宇宙の球体の軌道エネルギー=軌道のダークマターの数×1個のダークマターのエネルギー、です。
3. 各軌道の1個のダークマターのエネルギーはいくらか。
私は10月20日に提出した「ダークマター3」において、宇宙の時代における1個のダークマターが1秒間に作るエネルギーについて記した。
1個のダークマターが1秒間に作る磁気の光子のエネルギー=4.468×10−31−aJです。このエネルギーを1個のダークマターのエネルギーとします。
各軌道の1個のダークマターのエネルギーは4.468×10−31−aJです。
10−10mの場の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−10J=4.468×10−21J、です。
10−11mの場の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−11J=4.468×10−20J、です。
10−12mの場の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−12J=4.468×10−19J、です。
10−13mの場の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−13J=4.468×10−18J、です。
10−14mの場の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−14J=4.468×10−17J、です。
4. 地球の半径軌道と原子数はどのようであるか。
地球の中心に成ればなる程、場のエネルギーは高く原子の軌道は小さくなるから、半径のどの軌道においても存在する原子数は同じです。
半径にr個の原子が存在する。
地球の体積の原子数=地球の体積の原子数
4π÷3×r3=1.2×1057個
r3=1.2×1057個×3÷4π=2.866×1056個=288.6×1054
r=6.609×1018個
地球の赤道半径は、6378Kmです。
・半径軌道1000Kmに存在する原子数はいくらか。
半径軌道の原子数÷6.378=6.609×1018個÷6.378=1.036×1018個
半径軌道1000Kmに存在する原子数は1.036×1018個です。
5. 球体の宇宙の半径にはどれ位のダークマターが存在するか。球体の宇宙の半径軌道107光年にはいくらのダークマターが存在するか。
球体の宇宙の半径にr個のダークマターが存在するとする。
球体の宇宙の体積のダークマター数=全体の総ダークマター数
4÷3×πr3=1.077×1079個
r3=1.077×1079個÷(4÷3×π)=2.572×1078個
r=1.370×1026個
球体の宇宙の半径には1.370×1026個のダークマターが存在する。
・球体の宇宙の半径軌道107光年にはいくらのダークマターが存在するか。
球体の宇宙の半径には1.370×1026個のダークマターが存在する。
球体の宇宙の半径を5×107光年とする。
107光年には、1.370×1026個÷5=2.740×1025、個のダークマターが存在する。
球体の宇宙の半径軌道107光年には2.740×1025個のダークマターが存在する。
6. 宇宙の軌道の速度を全て、宇宙の軌道エネルギーの式で計算した、107光年の軌道エネルギーとし、速度2とする場合、1個のダークマターのエネルギーとこのダークマターが存在する場の電子のラブの公転軌道はいくらか。宇宙の軌道エネルギーの式で計算する、107光年の軌道エネルギーはいくらか。
・宇宙の軌道エネルギーの式で計算する、107光年の軌道エネルギーはいくらか。
宇宙の各軌道の軌道エネルギー=4.827×1027JKm÷軌道半径=4.827×1027JKm÷(107×9.64×1012Km)=5.103×107J
速度2=5.103×107Kmです。
全宇宙の速度2を5.103×107Jとする。
宇宙の各軌道の軌道エネルギー=軌道のダークマターの数×1個のダークマターのエネルギー=2.740×1025個×1個のダークマターのエネルギー=5.103×107J
1個のダークマターのエネルギー=5.103×107J÷(2.740×1025個)=1.862×10−18J
・この1個のダークマターのエネルギーは、どのエネルギーの場でできたものであるか。
4.468×10−31−aJ=1.862×10−18J
10−31−aJ=1.862×10−18J÷4.468=4.167×10−19J
10−aJ=4.167×10−19J×1031=4.167×1012=1012.620
a=-12.620
10−12.620m=10−13+0.38m=2.399×10−13m
このダークマターが存在する場は、2.399×10−13mです。
宇宙の軌道の速度を全て、宇宙の軌道エネルギーの式で計算した、107光年の軌道エネルギーとし、速度2とする場合、
軌道エネルギーは5.103×107Jで、速度は(5.103×107)1/2Km=7.144×103Km、です。
各軌道の速度が7.144×103Kmの場合、1個のダークマターのエネルギーは1.862×10−18Jです。
このダークマターは、2.399×10−13mの場に存在します。
この場の電子のラブの公転軌道は2.399×10−13mです。
7. 10−10m時代のダークマターが作る軌道の速度はいくらか。
10−10mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−10J=4.468×10−21J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−21J=1.224×105J
速度2=1.224×105Km
速度=(1.224×105Km)1/2=3.499×102Km
10−10mの時代のダークマターが作る軌道の速度は3.499×102Kmです。
8. 10−11m時代のダークマターが作る軌道の速度はいくらか。
10−11mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−11J=4.468×10−20J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−20J=1.224×106J
速度2=1.224×106Km
速度=(1.224×106Km)1/2=1.106×103Km
10−11mの時代のダークマターが作る軌道の速度は1.106×103Kmです。
9. 10−12m時代のダークマターが作る軌道の速度はいくらか。
10−12mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−12J=4.468×10−19J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−19J=1.224×107J
速度2=1.224×107Km
速度=(1.224×107Km)1/2=3.499×103Km
10. 10−13m時代のダークマターが作る軌道の速度はいくらか。
10−13mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−13J=4.468×10−18J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−18J=1.224×108J
速度2=1.224×108Km
速度=(1.224×108Km)1/2=1.106×104Km
10−13mの時代のダークマターが作る軌道の速度は1.106×104Kmです。
11. 10−14m時代のダークマターが作る軌道の速度はいくらか。
10−14mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−14J=4.468×10−17J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−17J=1.224×109J
速度2=1.224×109Km
速度=(1.224×109Km)1/2=3.499×104Km
10−14mの時代のダークマターが作る軌道の速度は3.499×104Kmです。
12. 10−15m時代のダークマターが作る軌道の速度はいくらか。
10−15mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−15J=4.468×10−16J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−16J=1.224×1010J
速度2=1.224×1010Km
速度=(1.224×1010Km)1/2=1.106×105Km
10−15mの時代のダークマターが作る軌道の速度は1.106×105Kmです。
13. 10−16m時代のダークマターが作る軌道の速度はいくらか。
10−16mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−16J=4.468×10−15J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−15J=1.224×1011J
速度2=1.224×1011Km
速度=(1.224×1011Km)1/2=3.499×105Km
10−16mの時代のダークマターが作る軌道の速度は3.499×105Kmです。この速度は光速以上です。
この事が意味する事。
1.10−16m時代はブラックホールの素子の時代であり、この環境では、軌道の速度はほぼ光速です。
14. 軌道の速度が光速である、3×105Kmである場は10amの値はいくらか。
速度=3×105Km
速度2=9×1010Km
軌道エネルギー=9×1010J=軌道のダークマターの数×1個のダークマターのエネルギー=2.740×1025個×1個のダークマターのエネルギー
1個のダークマターのエネルギー=9×1010J÷(2.740×1025個)=3.285×10−15J
4.468×10−31−aJ=3.285×10−15J
10−a=3.285×10−15J÷(4.468×10−31)=7.352×1015=1015.8664
10a=10-15.8664=10-16+0.3336=10-16×2.156
よって、この場は、2.156×10−16mの場です。
電子のラブの公転軌道が2.156×10−16mの場では、軌道の回転速度は光速です。
この場はブラックホールの場です。
電子のラブの公転軌道が2.156×10−16m以下の場では、軌道の回転速度は光速以上です。
15. 10−17m時代のダークマターが作る軌道の速度はいくらか。
10−17mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−17J=4.468×10−14J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−14J=1.224×1012J
速度2=1.224×1012Km
速度=(1.224×1012Km)1/2=1.106×106Km
10−17mの時代のダークマターが作る軌道の速度は1.106×106Kmです。
16. 10−18m時代のダークマターが作る軌道の速度はいくらか。
10−18mの時代の1個のダークマターのエネルギーは4.468×10−31−aJ=4.468×10−31−−18J=4.468×10−13J、です。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×4.468×10−13J=1.224×1013J
速度2=1.224×1013Km
速度=(1.224×1013Km)1/2=3.499×106Km
10−18mの時代のダークマターが作る軌道の速度は3.499×106Kmです。
17. 光速の2条の速さになる時代は何時か。
速度=9×1010Km
速度2=81×1020Km
軌道のエネルギー=81×1020J=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×1個のダークマターのエネルギー
1個のダークマターのエネルギー=81×1020J÷(2.740×1025個)=2.956×10−4J
4.468×10−31−aJ=2.956×10−4J
10−a=2.956×10−4J÷(4.468×10−31)=6.616×1026=1026.8206
10a=10-26.8206=10-27+0.1794=10-27×1.511
よって、この場は、1.511×10−27mの時代です。
18. 現代、宇宙の速度をWとする。この場合1個のダークマターのエネルギーはいくらか。
軌道のエネルギー=軌道のダークマター数×1個のダークマターのエネルギー=2.740×1025個×1個のダークマターのエネルギー=W2
1個のダークマターのエネルギー=W2÷(2.740×1025個)=W2×3.650×10−26(J)
現代、宇宙の速度をWとする。この場合1個のダークマターのエネルギーは、W2×3.650×10−26Jです。
19. 現代、宇宙の速度をWとする。この場の10aはいくらか。
1個のダークマターのエネルギー=4.468×10−31−aJ=W2×3.650×10−26J
10-a= W2×3.650×10−26J÷(4.468×10−31)=W2×8.169×104
a=−(Log W2×8.169×104)
この事によって理解できること。
宇宙の速度が大きい場(時代)は、10-aは小さいので、昔の時代であり、高エネルギーの時代です。
例えば、宇宙の速度が、103Kmである場合。
1個のダークマターのエネルギー=W2×3.650×10−26J=106×3.650×10−26J=3.650×10−20J
この場の10−a=106×8.169×104=1010.9122
10a=10-10.9122=10-11+0.0878=10-11×1.020
この場は1.020×10−11mの場です。この場は電子のラブの公転軌道が1.020×10−11mの場です。
・このように、10amの表現は時代を表現する場合と場のエネルギーを表現する場合にも用いられる。
これらのことを表に示す。
表1
|
時代や |
1個のダークマターのエネルギー=1秒間にできる磁気の光子のエネルギー |
軌道のダークマター数 |
軌道のエネルギー |
速度2 |
速度 |
|
10am
|
4.468×10−31−aJ |
2.740×1025個 |
1.224×10−5−aJ |
1.224×10−5−aKm |
(1.224×10−5−aKm)1/2 |
|
10−10m |
4.468×10−21J |
2.740×1025個 |
1.224×105J |
1.224×105Km |
3.499×102Km |
|
1.020×10−11m |
3.650×10−20J |
2.740×1025個 |
106J |
106Km |
103Km |
|
10−11m |
4.468×10−20J |
2.740×1025個 |
1.224×106J |
1.224×106Km |
1.106×103Km |
|
10−12m |
4.468×10−19J |
2.740×1025個 |
1.224×107J |
1.224×107Km |
3.499×103Km |
|
10−13m |
4.468×10−18J |
2.740×1025個 |
1.224×108J |
1.224×108Km |
1.106×104Km |
|
2.399×10−13m |
1.862×10−18J |
2.740×1025個 |
5.103×107J |
5.103×107Km |
7.144×103Km |
|
10−14m |
4.468×10−17J |
2.740×1025個 |
1.224×109J |
1.224×109Km |
3.499×104Km |
|
10−15m |
4.468×10−16J |
2.740×1025個 |
1.224×1010J |
1.224×1010Km |
1.106×105Km |
|
10−16m時代 |
4.468×10−15J |
2.740×1025個 |
1.224×1011J |
1.224×1011Km |
3.499×105Km |
|
2.156×10−16m |
3.285×10−15J |
2.740×1025個 |
9×1010J |
9×1010Km |
3×105Km |
|
10−17m |
4.468×10−14J |
2.740×1025個 |
1.224×1012J |
1.224×1012Km |
1.106×106Km |
|
10−18m時代 |
4.468×10−13J |
2.740×1025個 |
1.224×1013J |
1.224×1013Km |
3.499×106Km |
|
1.511×10−27m |
2.956×10−4J |
2.740×1025個 |
81×1020J |
81×1020Km |
9×1010Km |
|
a=-Log(W2×8.169×104) |
W2×3.650×10−26J |
2.740×1025個 |
W2J |
W2Km |
W |
・この考えの問題点
しかし、ダークマターは移動するので軌道のダークマターの数は一定でない。
20. 私は、20012年12月19日に提出した特願2012−276300において、ダークマターのエネルギーを7.96×107回の自転でできる磁気の光子のエネルギーが1束になっていると考え、これがダークマターのエネルギーであると考えました。
今回、私は、1個のダークマターのエネルギーは、ダークマターが1秒間に作るエネルギーであると考えます。
10−14m時代のダークマターのエネルギー=4.468×10−17Jとして考える。
それで、この考えに基づき特願2012−276300を再考察します。
21. 宇宙の速度がどの軌道でも同じ速度であるとすると、宇宙の軌道にはどれくらいのダークマターが存在するか。これは、特願2012−276300の「請求項9」です。
宇宙の軌道のエネルギーは、4.827×1027JKm÷距離。
・半径107光年の軌道の場合。
軌道のエネルギーのa倍のエネルギーが速度を作っているとする。
軌道のエネルギー=4.827×1027JKm÷距離=4.827×1027JKm÷(107×9.46×1012Km
)=5.103×107J。
軌道のダークマターの数=5.103×107J×a÷(1個のダークマターのエネルギー)=5.103×107×a÷(4.468×10−17J)=5.103×107×a×2.238×1016=1.142×1024×a(個)
・半径2×107光年の軌道の場合。
軌道のエネルギーのb倍のエネルギーが速度を作っているとする。
軌道のエネルギー=4.827×1027JKm÷距離=4.827×1027JKm÷(2×107×9.46×1012Km
)=2.551×107J。
軌道のダークマターの数=2.551×107J×b÷(4.468×10−17J)=2.552×107J×b×2.238×1016=5.711×1023×b(個)
・半径3×107光年の軌道の場合。
軌道のエネルギーのc倍のエネルギーが速度を作っているとする。
軌道のエネルギー=4.827×1027JKm÷距離=4.827×1027JKm÷(3×107×9.46×1012Km
)=1.701×107J。
軌道のダークマターの数=1.701×107J×c÷(4.468×10−17J)=1.701×107J×c×2.238×1016=3.807×1023×c(個)
・半径4×107光年の軌道の場合。
軌道のエネルギーのd倍のエネルギーが速度を作っているとする。
軌道のエネルギー=4.827×1027JKm÷距離=4.827×1027JKm÷(4×107×9.46×1012Km
)=1.276×107J。
軌道のダークマターの数=1.276×107J×d÷(4.468×10−17J)=1.276×107J×d×2.238×1016=2.856×1023×d(個)
・半径5×107光年の軌道の場合。
軌道のエネルギーのe倍のエネルギーが速度を作っているとする。
軌道のエネルギー=4.827×1027JKm÷距離=4.827×1027JKm÷(5×107×9.46×1012Km
)=1.021×107J。
・軌道のダークマターの数=1.021×107J×e÷(4.468×10−17J)=1.021×107J×e×2.238×1016=2.285×1023×e(個)
22. 各軌道の速度が同じである場合、a,b,c,d,eの比はいくらか。これは特願2012−276300の「請求項10」です。
速度2=5.103×107J×a=2.552×107J×b=1.701×107J×c=1.276×107J×d=1.021×107J×e
a:b:c:d:e=1:2:3:4:5
23. 例えば、速度=(5.103×107)1/2Km=7.144×103Km、である場合、各軌道のダークマター数はいくらか。これは特願2012−276300の「請求項11」です。
・107光年の軌道のダークマターの数は、1.142×1024×1個=1.142×1024個です。
・2×107光年の軌道のダークマターの数は、5.711×1023個×2=1.142×1024個です。
・3×107光年の軌道のダークマターの数は、3.807×1023個×3=1.142×1024個です。
・4×107光年の軌道のダークマターの数は、2.856×1023個×4=1.142×1024個です。
・5×107光年の軌道のダークマターの数は、2.285×1023個×5=1.143×1024個です。
これらの10−14m時代の宇宙は円錐台のような形として観察される。
このことを表に示す。
表2
|
軌道半径 |
軌道のエネルギー |
速度 |
速度2 |
軌道のエネルギー |
ダークマター1個が1秒に作るエネルギー |
ダークマターの数 |
ダークマターの数 |
速度2 |
ダークマターの数 |
|
107光年 |
5.103×107J |
7.144×103Km |
5.103×107Km |
5.103×107J |
4.468×10−17J |
1.142×1024×a個 |
1.142×1024個 |
V2Km |
2.238×1016×V2 個 |
|
2×107光年 |
2.551×107J |
5.052×103Km |
5.103×107Km |
5.103×107J |
4.468×10−17J |
5.712×1023×b個 |
1.142×1024個 |
V2Km |
2.238×1016×V2 個 |
|
3×107光年 |
1.701×107J |
4.124×103Km |
5.103×107Km |
5.103×107J |
4.468×10−17J |
3.807×1023×c個 |
1.142×1024個 |
V2Km |
2.238×1016×V2 個 |
|
4×107光年 |
1.276×107J |
3.572×103Km |
5.103×107Km |
5.103×107J |
4.468×10−17J |
2.856×1023×d個 |
1.142×1024個 |
V2Km |
2.238×1016×V2 個 |
|
5×107光年 |
1.021×107J |
1.010×103Km |
5.103×107Km |
5.103×107J |
4.468×10−17J |
2.285×1023×e個 |
1.142×1024個 |
V2Km |
2.238×1016×V2 個 |
24. 宇宙の端の軌道が加速膨張をするためには、ダークマターの数はどれ位でなければならないか。これは特願2012−276300の「請求項12」です。
宇宙の端の軌道の半径が5×107光年であるとする。
107光年から4×107光年の間は等速で、速度がVKmであるとする。その場合、各軌道のダークマターの数は2.238×1016×V2個です。
それで、ダークマター数がこれ以上の場合、速度はVKm以上になる。
宇宙の端の軌道が加速膨張をするためには、ダークマターの数は2.238×1016×V2個以上でなければならない。
これらの宇宙の形は、現代の宇宙はラッパの口のような宇宙です。
25. 宇宙の端の軌道の加速がV52Kmである場合、この軌道のダークマターの数はいくらか。これは特願2012−276300の「請求項13」です。
宇宙の端の軌道の加速がV52Kmであるから、その軌道のダークマターの数は2.238×1016×V52個です。
26. どうして宇宙の端の軌道が加速膨張をしているのか。これは特願2012−276300の「請求項14」です。
宇宙の中心のブラックホールを中心に回転している。ダークマターには質量がある。
それで、遠心力が働きダークマターは中心から遠くの方に移動する。
そのため、宇宙の大きい軌道のダークマターの数は小さい軌道のダークマターの数より多くなる。
よって、107光年の軌道のダークマターの数<2×107光年の軌道のダークマターの数<3×107光年の軌道のダークマターの数<4×107光年の軌道のダークマターの数<5×107光年の軌道のダークマターの数<6×107光年の軌道のダークマターの数<7×107光年の軌道のダークマター数、です。
速度は、107光年の軌道の速度<2×107光年の軌道の速度<3×107光年の軌道の速度<4×107光年の軌道の速度<5×107光年の軌道の速度<6×107光年の軌道の速度<7×107光年の軌道の速度、です。
107光年の軌道の速度をV1とし、2×107光年の軌道の速度をV2とし、3×107光年の軌道の速度をV3とし、4×107光年の軌道の速度をV4とし、5×107光年の軌道の速度をV5とし、6×107光年の軌道の速度をV6とし、7×107光年の軌道の速度をV7とする。
V1< V2< V3< V4< V5<
V6< V7、です。
107光年の軌道のダークマターの数は、2.238×1016×V12個です。
2×107光年の軌道のダークマターの数は、2.238×1016×V22個です。
3×107光年の軌道のダークマターの数は、2.238×1016×V32個です。
4×107光年の軌道のダークマターの数は、2.238×1016×V42個です。
5×107光年の軌道のダークマターの数は、2.238×1016×V52個です。
6×107光年の軌道のダークマターの数は、2.238×1016×V62個です。
7×107光年の軌道のダークマターの数は、2.238×1016×V72個です。
この宇宙の形は“横膨張の宇宙”です。
これからの宇宙は加速膨張宇宙になるでしょう。なぜなら、ダークマターは移動し続けるからです。
このことを表に示す。
表3
|
軌道半径 |
速度 |
速度2 |
軌道のダークマターの数 |
|
107光年 |
V1Km |
V12Km |
2.238×1016×V12個 |
|
2×107光年 |
V2Km |
V22Km |
2.238×1016×V22個 |
|
3×107光年 |
V3Km |
V32Km |
2.238×1016×V32個 |
|
4×107光年 |
V4Km |
V42Km |
2.238×1016×V42個 |
|
5×107光年 |
V5Km |
V52Km |
2.238×1016×V52個 |
|
6×107光年 |
V6Km |
V62Km |
2.238×1016×V62個 |
|
7×107光年 |
V7Km |
V72Km |
2.238×1016×V72個 |
27. 泡宇宙の場合はどのようであるか。これは特願2012−276300の「請求項15」です。
私は、2012年6月13日に提出した、特願2012−133515、「宇宙の軌道エネルギーと泡状銀河集団の回転」に於いて、泡宇宙について次のように記した。
中心が1011太陽質量のブラックホールでできた泡状の銀河集団の軌道半径と軌道エネルギーと速度
表4
|
時代 |
軌道エネルギーの式 |
泡状の銀河達の軌道半径=ジェットが届いた距離 |
銀河達の軌道エネルギー |
銀河達の速度 |
|
10−16m |
1.171×1026JKm÷軌道半径 |
3.006×1017Km=3.178×104光年 |
3896×108J |
1.974×104Km |
|
10−15m |
1.171×1026JKm÷軌道半径 |
3.006×1018Km=3.178×105光年 |
3.896×107J |
6.242×103Km |
|
10−14m |
1.171×1026JKm÷軌道半径 |
3.006×1019Km=3.178×106光年 |
3.896×106J |
1.974×103Km |
中心が1010太陽質量のブラックホールでできた泡状の銀河集団の軌道半径と軌道エネルギーと速度
表5
|
時代 |
軌道エネルギーの式 |
泡状の銀河達の軌道半径=ジェットが届いた距離 |
銀河達の軌道エネルギー |
銀河達の速度 |
|
10−16m |
2.524×1025JKm÷軌道半径 |
1.395×1017Km=1.475×104光年 |
1.809×108J |
1.345×104Km |
|
10−15m |
2.524×1025JKm÷軌道半径 |
1.395×1018Km=1.475×105光年 |
1.809×107J |
4.253×103Km |
|
10−14m |
2.524×1025JKm÷軌道半径 |
1.395×1019Km=1.475×106光年 |
1.809×106J |
1.345×103Km |
中心が109太陽質量のブラックホールでできた泡状の銀河集団の軌道半径と軌道エネルギーと速度
表6
|
時代 |
軌道エネルギーの式 |
泡状の銀河達の軌道半径=ジェットが届いた距離 |
銀河達の軌道エネルギー |
銀河達の速度 |
|
10−16m |
5.438×1024JKm÷軌道半径 |
6.477×1016Km=6.847×103光年 |
8.396×107J |
9.163×103Km |
|
10−15m |
5.438×1024JKm÷軌道半径 |
6.477×1017Km=6.847×104光年 |
8.396×106J |
2.898×103Km |
|
10−14m |
5.438×1024JKm÷軌道半径 |
6.477×1018Km=6.847×105光年 |
8.396×105J |
9.163×102Km |
28. 泡の中心が1011太陽質量のブラックホールの場合。これは特願2012−276300の「請求項16」です。
その軌道エネルギーは、1.171×1026JKm÷軌道半径、です。
10−16m時代、ジェットは半径、3.006×1017Kmに届き、その軌道にクエーサー達を作り、
10−15m時代、その軌道は、3.006×1018Kmになり、銀河達の軌道となり、
10−14m時代、その軌道は、3.006×1019Kmになり、銀河達の軌道になっている。
その銀河達の軌道のエネルギーは、3.896×106Jで、銀河達の速度は、1.974×103Kmです。
(アンドロメガ銀河の速度のように考える。)
どこまでも、速度が1.974×103Kmであるならば、軌道のダークマターの数はいくらか。
軌道のダークマターの数=軌道のエネルギー÷10−14m時代のダークマターが1秒間に作る磁気の光子のエネルギー(1個のダークマターが1秒間に作るエネルギー)=V2J÷(4.468×10−17J)=2.238×1016×V2.
この式より、
軌道のダークマターの数=2.238×1016×(1.974×103)2=2.238×1016×3.897×106=8.721×1022(個)
どこまでも、速度が1.974×103Kmであるならば、軌道のダークマターの数は8.721×1022個です。
泡宇宙の端が加速膨張している場合、泡宇宙の端の軌道(銀河達の軌道)の速度がV11Kmであるとすると、ダークマターの数は、V112×2.238×1016個です。
29. 泡の中心が1010太陽質量のブラックホールの場合。これは特願2012−276300の「請求項17」です。
その軌道エネルギーは、2.524×1025JKm÷軌道半径、です。
10−16m時代、ジェットは半径、1.395×1017Kmに届き、その軌道にクエーサー達を作り、
10−15m時代、その軌道は、1.395×1018Kmになり、銀河達の軌道となり、
10−14m時代、その軌道は、1.395×1019Kmになり、銀河達の軌道になっている。
その銀河達の軌道のエネルギーは、1.809×106Jで、銀河達の速度は、1.345×103Kmです。
(アンドロメガ銀河の速度のように考える。)
どこまでも、速度が1.345×103Kmであるならば、軌道のダークマターの数はいくらか。
軌道のダークマターの数=2.238×1016×(1.345×103)2=2.238×1016×1.809×106=4.049×1022(個)
どこまでも、速度が1.345×103Kmであるならば、軌道のダークマターの数は4.049×1022個です。
泡宇宙の端が加速膨張している場合、泡宇宙の端の軌道(銀河達の軌道)の速度がV10Kmであるとすると、ダークマターの数は、V102×2.238×1016個です。
30. 泡の中心が109太陽質量のブラックホールの場合。これは特願2012−276300の「請求項18」です。
その軌道エネルギーは、5.438×1024JKm÷軌道半径、です。
10−16m時代、ジェットは半径、6.477×1016Kmに届き、その軌道にクエーサー達を作り、
10−15m時代、その軌道は、6.477×1017Kmになり、銀河達の軌道となり、
10−14m時代、その軌道は、6.477×1018Kmになり、銀河達の軌道になっている。
その銀河達の軌道のエネルギーは、8.396×105Jで、銀河達の速度は、9.163×102Kmです。
(アンドロメガ銀河の速度のように考える。)
どこまでも、速度が9.163×102Kmであるならば、軌道のダークマターの数はいくらか。
軌道のダークマターの数=2.238×1016×(9.163×102)2=2.238×1016×8.396×105=1.879×1022(個)
どこまでも、速度が9.163×102Kmであるならば、軌道のダークマターの数は1.879×1022個です。
泡宇宙の端が加速膨張している場合、泡宇宙の端の軌道(銀河達の軌道)の速度がV9Kmであるとすると、ダークマターの数は、V92×2.238×1016個です。
このことを表に示す。
表7
|
泡の中心のブラックホールの質量 |
軌道エネルギーの式 |
10−14m時代の銀河達の軌道 |
銀河達の軌道のエネルギー |
銀河達の速度 |
同じ速度の場合、軌道のダークマターの数 |
速度が変わる場合 |
ダークマターの数 |
|
1011太陽質量 |
1.171×1026JKm÷軌道半径 |
3.006×1019Km |
3.896×106J |
1.974×103Km |
8.721×1022個 |
V11Km |
V112×2.238×1016個 |
|
1010太陽質量 |
2.524×1025JKm÷軌道半径 |
1.395×1019Km |
1.809×106J |
1.345×103Km |
4.049×1022個 |
V10Km |
V102×2.238×1016個 |
|
109太陽質量 |
5.438×1024JKm÷軌道半径 |
6.477×1018Km |
8.396×105J |
9.163×102Km |
1.879×1022個 |
V9Km |
V92×2.238×1016個 |
(ダークマター1個のエネルギーとは、1個のダークマターが1秒間に作る光子のエネルギーです)
31. 半径107光年の軌道のダークマターの数:半径2×107光年の軌道のダークマターの数:半径3×107光年の軌道のダークマターの数:半径4×107光年の軌道のダークマターの数:半径5×107光年の軌道のダークマターの数=1:2:3:4:5、とした場合、各々の軌道のダークマター1個のエネルギーはどのようであるか。
半径107光年の軌道のダークマターの数:半径2×107光年の軌道のダークマターの数:半径3×107光年の軌道のダークマターの数:半径4×107光年の軌道のダークマターの数:半径5×107光年の軌道のダークマターの数=1:2:3:4:5
半径107光年の軌道の平均のダークマター数は2.740×1025個です。
半径5×107光年の軌道のダークマター数は、5×2.740×1025個=1.390×1026個です。
それで、
半径107光年の軌道のダークマターの数=1.390×1026個÷(1+2+3+4+5)=1.390×1026個÷15=9.267×1024個
半径2×107光年の軌道のダークマターの数=1.390×1026個÷(1+2+3+4+5)×2=1.390×1026個÷15×2=1.853×1025個
半径3×107光年の軌道のダークマターの数=1.390×1026個÷(1+2+3+4+5)×3=1.390×1026個÷15×3=2.780×1025個
半径4×107光年の軌道のダークマターの数=1.390×1026個÷(1+2+3+4+5)×4=1.390×1026個÷15×4=3.707×1025個
半径5×107光年の軌道のダークマターの数=1.390×1026個÷(1+2+3+4+5)×5=1.390×1026個÷15×5=4.634×1025個
・各々の軌道のダークマター1個のエネルギーはいくらか。
軌道のダークマター1個のエネルギー=速度2÷軌道のダークマターの数
半径107光年の軌道のダークマター1個のエネルギー=W2÷(9.267×1024個)=W2×1.079×10-25J
半径2×107光年の軌道の、ダークマター1個のエネルギー=W2÷(1.853×1025個)=W2×5.397×10-26J
半径3×107光年の軌道の、ダークマター1個のエネルギー=W2÷(2.780×1025個)=W2×3.597×10-26J
半径4×107光年の軌道の、ダークマター1個のエネルギー=W2÷(3.707×1025個)=W2×2.698×10-26J
半径5×107光年の軌道の、ダークマター1個のエネルギー=W2÷(4.634×1025個)=W2×2.158×10-26J
・各々の軌道のダークマターのエネルギーの比はいくらか。
W2×1.079×10-25J:W2×5.397×10-26J:W2×3.597×10-26J:W2×2.698×10-26J:W2×2.158×10-26J=5:2.501:1.667:1.250:1
半径107光年の軌道の、ダークマター1個のエネルギー:半径2×107光年の軌道の、ダークマター1個のエネルギー:半径3×107光年の軌道の、ダークマター1個のエネルギー:半径4×107光年の軌道の、ダークマター1半径個のエネルギー:半径5×107光年の軌道の、ダークマター1個のエネルギー=5:2.501:1.667:1.250:1
・軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=速度2=一定。このことが意味することは、何か。
軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=速度2=一定
この事が意味することは、速度が一定の場合、ダークマターの数とダークマター1個のエネルギーは反比例することです。
この事が意味することは、ダークマターの数の比×ダークマター1個のエネルギーの比=一定、です。
・各々の軌道のダークマターの数の比×ダークマター1個のエネルギーの比はどのようであるか。
半径107光年の軌道の場合。
ダークマターの数の比×ダークマター1個のエネルギーの比=1×5=5
半径2×107光年の軌道の場合。
ダークマターの数の比×ダークマター1個のエネルギーの比=2×2.501=5.002
半径3×107光年の軌道の場合。
ダークマターの数の比×ダークマター1個のエネルギーの比=3×1.667=5.001
半径4×107光年の軌道の場合。
ダークマターの数の比×ダークマター1個のエネルギーの比=4×1.250=5
半径5×107光年の軌道の場合。
ダークマターの数の比×ダークマター1個のエネルギーの比=5×1=5
このように、ダークマターの数の比×ダークマター1個のエネルギーの比=一定、です。
このことを表に示す。
表8
|
軌道半径 |
ダークマターの数の比 |
ダークマターの数 |
速度 |
速度2 |
軌道エネルギー |
ダークマター1個のエネルギー |
ダークマター1個のエネルギーの比 |
|
107光年 |
1 |
9.267×1024個 |
WKm |
W2Km |
W2J |
W2×1.079×10-25J |
5 |
|
2×107光年 |
2 |
1.853×1025個 |
WKm |
W2Km |
W2J |
W2×5.397×10-26J |
2.501 |
|
3×107光年 |
3 |
2.780×1025個 |
WKm |
W2Km |
W2J |
W2×3.597×10-26J |
1.667 |
|
4×107光年 |
4 |
3.707×1025個 |
WKm |
W2Km |
W2J |
W2×2.698×10-26J |
1.250 |
|
5×107光年 |
5 |
4.634×1025個 |
WKm |
W2Km |
W2J |
W2×2.158×10-26J |
1 |
ダークマター1個のエネルギーとは、1個のダークマターが1秒間に作る光子のエネルギーです。
32. 半径107光年の軌道のダークマター1個のエネルギー:半径2×107光年の軌道のダークマター1個のエネルギー:半径3×107光年の軌道のダークマター1個のエネルギー:半径4×107光年の軌道のダークマター1個のエネルギー:半径107光年の軌道のダークマター1個のエネルギー=5:4:3:2:1とする場合、ダークマター1個のエネルギーと、軌道のダークマターの数はいくらか。
宇宙の軌道が中央のダークマターに近いほど高エネルギーの場です。
それで、半径107Kmの軌道のダークマター1個のエネルギー:半径2×107光年の軌道のダークマター1個のエネルギー:半径3×107光年の軌道のダークマター1個のエネルギー:半径4×107光年の軌道のダークマター1個のエネルギー:軌道半径107光年のダークマター1個のエネルギー=5:4:3:2:1とする。
・半径107光年の軌道のダークマター1個のエネルギーは、W2×1.079×10-25Jで、半径5×107光年の軌道のダークマター1個のエネルギーはW2×2.158×10-26J
、です。この比は、5:1です。
それで、ダークマターの1個のエネルギーの比を、5:4:3:2:1とする場合のダークマター1個のエネルギーはいくらか。
半径107光年のダークマター1個のエネルギー=W2×1.079×10-25J
半径2×107光年の軌道のダークマター1個のエネルギー=W2×2.158×10-26J×4=W2×8.632×10-26J
半径3×107光年の軌道のダークマター1個のエネルギー=W2×2.158×10-26J×3=W2×6.474×10-26J
半径4×107光年の軌道のダークマター1個のエネルギー=W2×2.158×10-26J×2=W2×4.316×10-26J
半径5×107光年の軌道のダークマター1個のエネルギー=W2×2.158×10-26J
・軌道のダークマターの数はいくらか。
軌道のダークマターの数=速度2÷軌道のダークマター1個のエネルギー
半径107光年の軌道ダークマターの数=W2÷(W2×1.079×10-25J)=9.268×1024(個)
半径2×107光年の軌道のダークマターの数=W2÷(W2×8.632×10-26J)=1.158×1025(個)
半径3×107光年の軌道のダークマターの数=W2÷(W2×6.474×10-26J)=1.545×1025(個)
半径4×107光年の軌道のダークマターの数=W2÷(W2×4.316×10-26J)=2.317×1025(個)
半径5×107光年の軌道のダークマターの数=W2÷(W2×2.158×10-26J
)=4.634×1025(個)
・軌道のダークマターの数の比はいくらか。
9.268×1024個:1.158×1025個:1.158×1025個:2.317×1025個:4.634×1025個=1:1.249:1.667:2.5:5
・各々の軌道のダークマター1個のエネルギーの比×ダークマターの数の比はどのようであるか。
5×1:4×1.249:3×1.667:3×1.667:2×2.5:1×5=5:4.996:5.001:5:
このことを表に示す。
表9
|
軌道半径 |
ダークマター1個のエネルギーの比 |
ダークマター1個のエネルギー |
速度 |
速度2 |
軌道エネルギー |
ダークマターの数 |
ダークマターの数の比 |
|
107光年 |
5 |
W2×1.079×10-25J |
WKm |
W2Km |
W2J |
9.268×1024個 |
1 |
|
2×107光年 |
4 |
W2×8.632×10-26J |
WKm |
W2 Km |
W2J |
1.158×1025個 |
1.249 |
|
3×107光年 |
3 |
W2×6.474×10-26J |
WKm |
W2 Km |
W2J |
1.545×1025個 |
1.667 |
|
4×107光年 |
2 |
W2×4.316×10-26J |
WKm |
W2 Km |
W2J |
2.317×1025個 |
2.5 |
|
5×107光年 |
1 |
W2×2.158×10-26J |
WKm |
W2 Km |
W2J |
4.634×1025個 |
5 |
ダークマター1個のエネルギーとは、1個のダークマターが1秒間に作る光子のエネルギーです。
この事によって何が理解できるか。
1.この表があると、ほとんどすべての軌道のダークマター1個のエネルギーとダークマターの数が理解できる。
宇宙のどこまでも速度が同じ場合、軌道の速度がWKmの場合、半径3×107光年の軌道のダークマター1個のエネルギーはW2×6.474×10-26Jである。半径5×107光年の軌道のダークマター1個のエネルギーはその1/3で、W2×2.158×10-26Jです。半径4.5×107光年の軌道のダークマター1個のエネルギーはその1.5/3=1/2のエネルギーです。
33. 宇宙の速度を3×102Kmであるとする場合、各々の軌道のダークマターの数と、ダークマター1個のエネルギーはいくらか。各々の軌道のダークマターの数を1:2:3:4:5とする。
・半径107光年の軌道のダークマターの数は9.267×1024個です。
速度2=軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=9.267×1024個×ダークマター1個のエネルギー=(3×102Km)2
ダークマター1個のエネルギー=9×104÷(9.267×1024個)=9.712×10-21J
半径107光年の軌道のダークマターの数は9.267×1024個で、ダークマター1個のエネルギーは9.712×10-21Jです。
・半径2×107光年の軌道のダークマター数は1.853×1025個です。
速度2=軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=1.853×1025個×ダークマター1個のエネルギー=(3×102Km)2
ダークマター1個のエネルギー=9×104÷(1.853×1025個)=4.857×10-21J
半径2×107光年の軌道のダークマターの数は1.853×1025個で、ダークマター1個のエネルギーは4.857×10-21Jです。
・半径3×107光年の軌道のダークマター数は2.780×1025個です。
速度2=軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=2.780×1025個×ダークマター1個のエネルギー=(3×102Km)2
ダークマター1個のエネルギー=9×104÷(2.780×1025個)=3.237×10-21J
半径3×107光年の軌道のダークマターの数は2.780×1025個で、ダークマター1個のエネルギーは3.237×10-21Jです。
・半径4×107光年の軌道のダークマター数は3.707×1025個です。
速度2=軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=3.707×1025個×ダークマター1個のエネルギー=(3×102Km)2
ダークマター1個のエネルギー=9×104÷(3.707×1025個)=2.428×10-21J
半径4×107光年の軌道のダークマターの数は3.707×1025個で、ダークマター1個のエネルギーは2.428×10-21Jです。
・半径5×107光年の軌道のダークマター数は4.634×1025個です。
速度2=軌道のエネルギー=ダークマターの数×ダークマター1個のエネルギー=2.780×1025個×ダークマター1個のエネルギー=(3×102Km)2
ダークマター1個のエネルギー=9×104÷(4.634×1025個)=1.942×10-21J
半径5×107光年の軌道のダークマターの数は4.634×1025個で、ダークマター1個のエネルギーは1.942×10-21Jです。
このことを表に示す。
表10
|
軌道半径 |
軌道のダークマターの数の比 |
軌道のダークマターの数 |
速度 |
速度2 |
軌道エネルギー |
ダークマター1個のエネルギー |
ダークマター1個のエネルギーの比 |
|
107光年 |
1 |
9.267×1024個 |
3×102Km |
9×104Km |
9×104J |
9.712×10-21J |
5 |
|
2×107光年 |
2 |
1.853×1025個 |
3×102 Km |
9×104Km |
9×104J |
4.857×10-21J |
2.501 |
|
3×107光年 |
3 |
2.780×1025個 |
3×102 Km |
9×104Km |
9×104J |
3.237×10-21J |
1.667 |
|
4×107光年 |
4 |
3.707×1025個 |
3×102 Km |
9×104Km |
9×104J |
2.428×10-21J |
1.250 |
|
5×107光年 |
5 |
4.634×1025個 |
3×102 Km |
9×104Km |
9×104J |
1.942×10-21J |
1 |
34. 宇宙の速度を3×102Kmであるとする場合、各々の軌道のダークマターの数と、ダークマター1個のエネルギーはいくらか。各々の軌道のダークマター1個のエネルギーを5:4:3:2:1とする。
宇宙の速度=3×102Km。宇宙の速度2=9×104Km。軌道エネルギー=9×104J
半径107光年の軌道のダークマターの数は9.267×1024個ですから、
半径107光年の軌道エネルギー=9×104J=軌道のダークマターの数×軌道のダークマター1個のエネルギー=9.267×1024個×軌道のダークマター1個のエネルギー
軌道のダークマター1個のエネルギー=9×104J÷(9.267×1024個)=9.712×10-21J
半径107光年の軌道のダークマター1個のエネルギー=9.712×10-21J
それで、
半径2×107光年の軌道のダークマター1個のエネルギー=9.712×10-21J×0.8=7.770×10-21J
半径3×107光年の軌道のダークマター1個のエネルギー=9.712×10-21J×0.6=5.827×10-21J
半径4×107光年の軌道のダークマター1個のエネルギー=9.712×10-21J×0.4=3.885×10-21J
半径5×107光年の軌道のダークマター1個のエネルギー=9.712×10-21J×0.2=1.942×10-21J
各々の軌道のダークマターの数
軌道のダークマターの数=速度2÷軌道のダークマター1個のエネルギー
半径107光年の軌道のダークマターの数=9.267×1024個
半径2×107光年の軌道のダークマターの数=9×104J÷(7.770×10-21J)=1.158×1025(個)
半径3×107光年の軌道のダークマターの数=9×104J÷(5.827×10-21J)=1.545×1025(個)
半径4×107光年の軌道のダークマターの数=9×104J÷(3.885×10-21J)=2.317×1025(個)
半径5×107光年の軌道のダークマターの数=9×104J÷(1.942×10-21J)=4.634×1025(個)
・このダークマターの10amはいくらか。
1個のダークマターが1秒間に作る磁気の光子のエネルギー=4.468×10−31−aJです。このエネルギーを1個のダークマターのエネルギーとします。
半径107光年の軌道のダークマター1個のエネルギー=9.712×10-21J=4.468×10−31−aJ
10−a=9.712×10-21J÷(4.468×10−31J)=2.174×1010=Log2.174×1010=100.3373×1010=1010.3373
10a=10-10.3373=10-11×100.6627=4.599×10-11
半径107光年の軌道のダークマターは電子のラブの公転軌道が4.599×10-11mの場に存在します。
半径107光年の軌道は、電子のラブの公転軌道が4.599×10-11mの場です。
半径2×107光年の軌道のダークマター1個のエネルギー=7.770×10-21J=4.468×10−31−aJ
10−a=7.770×10-21J÷(4.468×10−31)=1.739×1010=Log1.739×1010=100.2402+10=1010.2402
10a=10-10.2402=10-11+0.7598=5.751×10-11
半径2×107光年の軌道のダークマターは電子のラブの公転軌道が5.751×10-11mの場に存在します。
半径2×107光年の軌道は、電子のラブの公転軌道が5.751×10-11mの場です。
半径3×107光年の軌道のダークマター1個のエネルギー=5.827×10-21J=4.468×10−31−aJ
10−a=5.827×10-21J÷(4.468×10−31J)=1.304×1010=Log1.304×1010=100.1152+10=1010.1152
10a=10-10.1152=10-11×100.8848=7.670×10-11
半径3×107光年の軌道のダークマターは電子のラブの公転軌道が7.670×10-11mの場に存在します。
半径3×107光年の軌道は、電子のラブの公転軌道が7.670×10-11mの場です。
半径4×107光年の軌道のダークマター1個のエネルギー=3.885×10-21J=4.468×10−31−aJ
10−a=3.885×10-21J÷(4.468×10−31J)=8.695×109=Log8.695×109=100.9393+9=109.9393
10a=10-9.9393=10-10+0.0607=1.014×10-10
半径4×107光年の軌道のダークマターは電子のラブの公転軌道が1.014×10-10mの場に存在します。
半径4×107光年の軌道は、電子のラブの公転軌道が1.014×10-10mの場です。
半径5×107光年の軌道のダークマター1個のエネルギー=1.942×10-21J=4.468×10−31−aJ
10−a=1.942×10-21J÷(4.468×10−31)=4.346×109=Log4.346×109=100,6381+9=109.6381
10a=10 -9.6381=10-10+0.3619=2.301×10-10
半径5×107光年の軌道のダークマターは電子のラブの公転軌道が2.301×10-10mの場に存在します。
半径5×107光年の軌道は、電子のラブの公転軌道が2.307×10-10mの場です。
・ダークマターの数の比×ダークマター1個のエネルギーの比=5×1:4×1.250:3×1.667:2×2.500:1×5.001=5:5:5:5:5
このことを表に示す。
表11
|
軌道半径 |
ダークマター1個のエネルギーの比 |
ダークマター1個のエネルギー |
速度 |
速度2 |
軌道エネルギー |
軌道のダークマターの数 |
軌道のダークマターの数の比 |
軌道の10am |
|
107光年 |
5 |
9.712×10-21J |
3×102Km |
9×104Km |
9×104J |
9.267×1024個 |
1 |
4.599×10-11m |
|
2×107光年 |
4 |
7.770×10-21J |
3×102Km |
9×104Km |
9×104J |
1.158×1025個 |
1.250 |
5.751×10-11m |
|
3×107光年 |
3 |
5.827×10-21J |
3×102Km |
9×104Km |
9×104J |
1.545×1025個 |
1.667 |
7.670×10-11m |
|
4×107光年 |
2 |
3.885×10-21J |
3×102Km |
9×104Km |
9×104J |
2.317×1025個 |
2.500 |
1.014×10-10m |
|
5×107光年 |
1 |
1.942×10-21J |
3×102Km |
9×104Km |
9×104J |
4.634×1025個 |
5.001 |
2.301×10-10m |
【図面の簡単な説明】
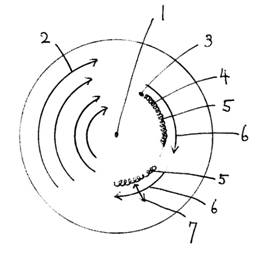
【図1】図1は、ダークマターが宇宙の回転速度を作る原理を示す。
宇宙の中心のブラックホールは軌道エネルギーを作りこの軌道エネルギーにより軌道は回転する。軌道にはダークマターが存在する。ダークマターは質量があるので軌道上を回転する。ダークマターが宇宙の軌道を回転することにより、ダークマターは電気のエネルギーを作る。これは、電子のラブが自転しながら公転することによって、磁気の光子と電気の光子を作っているのと同じ事です。ダークマターは自転だけしている電子のラブですから、自転している電子のラブ(ダークマター)が走ることによって、電気の光子ができる。この電気の光子のエネルギーが軌道の速度2を作っている。
【符号の説明】
1. 宇宙の中心のブラックホール
2. 軌道の回転
3. ダークマター
4. ダークマターは自転しながら回転する
5. ダークマターは自転して磁気の光子を作り、回転し、電気の光子を作る
6. 電気の光子は軌道のエネルギーとなり、速度2になる。
7. 磁気の光子
【書類名】図面
【図1】
【先行技術文献】
【特許文献1】特願2012−219904
【特許文献2】特願2012−227767
【特許文献3】特願2012−232448
【特許文献4】特願2012−276300