2011年3月の日本天文学会　　ｂ
タイトル「天王星の自転軸が公転面に対して98度傾いているのはなぜか」

 

　銀河系の腕は、銀河系の中心のブラックホールの影響より、もっと近い腕の中心のブラックホールの影響を受けるため、腕の中心のブラックホールを中心に螺旋回転している。これと同じように、天王星は、太陽の影響より、自分の中心の影響を受けている。そのため、天王星は螺旋回転をしている。天王星の公転の軌道エネルギー＝公転速度²＝6.81²Ｊ＝46.376Ｊ。天王星の螺旋回転速度²＝公転速度²×79.7＝46.376Km×79.7＝3696.175Km。天王星の螺旋回転速度＝(3696.175)^1/2Km/s=60.796Km/s。天王星は秒速60.796Kmで螺旋回転しながら、太陽の周りを、秒速6.81Kmで公転している。螺旋回転の軌道エネルギー＝螺旋回転する物体の表面の原子数×1個の原子が作る電気の光子1個のエネルギーです。天王星の表面の原子数は6.909×10³⁵個です。天王星の螺旋回転の軌道エネルギー＝螺旋回転速度²＝60.796²Ｊ＝3696.175J＝天王星の表面の原子数×1個の原子が1公転で作る電気の光子１個のエネルギー。1個の原子が1公転で作る電気の光子１個のエネルギー＝3.691×10³Ｊ÷(6.909×10³⁵個)＝5.35×10⁻³³Ｊ。1個の原子で、5.35×10⁻³³Ｊの電気の光子ができる。電気の光子の軌道＝1.233×10⁻⁴¹Ｊｍ÷電気の光子１個のエネルギー＝1.233×10⁻⁴¹Ｊｍ÷(5.35×10⁻³³Ｊ)＝2.3×10⁻⁹ｍ。電子のラブの公転軌道は、電気の光子の軌道に等しいから、この電子のラブの公転軌道は、2.3×10⁻⁹ｍです。・この場のＡはいくらか。Aは地表の何倍のエネルギーかを示す。地表の電子のラブの公転軌道÷A＝1.058×10⁻¹⁰ｍ÷Ａ＝2.3×10⁻⁹ｍ。Ａ＝1.058×10⁻¹⁰ｍ÷(2.3×10⁻⁹ｍ)＝4.6×10⁻²。・この場の温度はいくらか。温度＝Ａ²＝(4.6×10⁻²)²＝2.116×10⁻³＝0.002116(℃)。この場の温度は、0.002116℃です。この温度の値は、天王星が太陽から受ける福射量は、地球を1とすると、0.0027とほぼ等しい。
説明
１．　天王星の自転軸が公転面に垂直な線に対して98度傾いているのはなぜか。
２．　海王星の自転軸が公転面に垂直な線に対して28.8度傾いているのはなぜか。
　銀河系の腕は、銀河系の中心のブラックホールの影響により、もっと近い腕の中心のブラックホールの影響を受けるため、腕の中心のブラックホールを中心に螺旋回転している。これと同じように、天王星や海王星は、太陽から遠く離れているため、太陽の影響より、自分の中心の金属水素の影響を受けている。そのため、天王星と海王星は螺旋回転をしている。

 

図

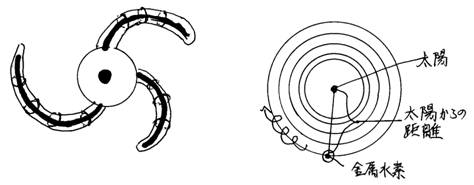
私は、ポスター講演で、第1世代の星がブラックホールであった時、“第1世代の木星”“第1世代の土星”“第1世代の天王星”“第1世代の海王星”ができた事を記した。

この事を表に示す。

	“第1世代の木星”	“第1世代の土星”	“第1世代の天王星”	“第1世代の海王星”
軌道引力でできた第1世代の惑星の質量	地球の136倍	地球の40倍	地球の9.77倍	地球の4.31倍
第1世代の惑星の状態	金属水素	金属水素	金属水素	金属水素
第1世代の惑星の質量は、現在の惑星の質量の何パーセントか。	地球の136倍÷地球の317.83倍×100＝42.79％	地球の40倍÷地球の95.16倍×100＝42.03％	地球の9.77倍÷地球の14.54倍×100＝67.19％	地球の4.31倍÷地球の17.15倍×100＝25.13％

天王星と海王星は螺旋回転しています。
天王星と海王星は、太陽より遠く離れているので、自分の中央に存在する金属水素の質量の影響を強く受けています。そして、太陽からの影響を受けています。
それが自転軸の傾きに現れています。

自転軸の傾きは、中央部の金属水素の質量÷太陽からの距離、に比例する。
自転軸の傾き＝定数×金属水素の質量が地球質量の何倍であるか÷惑星と太陽の間の距離、
この式で表す。

天王星の場合。

天王星の自転軸は公転軌道面に垂直な直線に対して98度傾いている。
天王星の中央の金属水素の質量は地球の質量の9.77倍です。そして、太陽からの距離は、28.750×10⁸Kmです。
98度＝K×9.77÷(28.750×10⁸Km)
K=98度×28.750×10⁸Km÷9.77＝288.383×10⁸Km度
Kの値は288.383×10⁸Km度です。
海王星の場合。
海王星の自転軸は公転軌道面に垂直な直線に対して28.8度傾いている。
海王星の中央の金属水素の質量は地球の質量の4.31倍です。そして、太陽からの距離は、45.044×10⁸Kmです。
Kの値を288.383×10⁸Km度とすると、海王星の自転軸は公転軌道面に垂直な直線に対して何度傾いているか。
K=288.383×10⁸Km度＝X×45.044×10⁸Km÷4.31
X=288.383×10⁸Km度×4.31÷(45.044×10⁸Km)＝27.59度
27.59度傾いている。
よって、螺旋回転している惑星の自転軸の公転軌道面に垂直な直線に対する傾きは、
自転軸の傾き＝定数×金属水素の質量が地球質量の何倍であるか÷惑星と太陽の間の距離＝288.383×10⁸Km度×金属水素の質量が地球質量の何倍であるか÷惑星と太陽の間の距離、の式で表される。
海王星の傾きを中心に考えると定数は、300.99×10⁸Kｍ度であり、天王星の傾きは102度です。

定数	傾き
288.383×108Kｍ度	天王星は98度 海王星は27.59度
300.99×108Kｍ度	天王星は102.28度 海王星は28.8度

 

３．　天王星はどのように螺旋回転しているか。
・惑星の公転軌道エネルギーは公転速度²である。この事に関しては次回説明する。

それで、
天王星の公転の軌道エネルギー＝公転速度²＝6.81²Ｊ＝46.376Ｊ。
・螺旋回転速度²＝公転速度²×79.7である。

螺旋回転の速度²は公転速度²の何倍か。

小さい腕は、（1569Km/s）²÷（175.8Km/s）²=2.462×10⁶÷（3.091×10⁴）＝79.65倍。

中位の腕は、（2354Km/s）²÷（263.7Km/s）²=5.541×10⁶÷（6.954×10⁴）＝79.68倍。

大きい腕は、（3138.7Km/s）²÷（351.6Km/s）²=9.851×10⁶÷（1.236×10⁵）＝79.70倍。

螺旋回転の速度²は、公転の速度²の79.68倍です。

それで、

天王星の螺旋回転速度²＝公転速度²×79.7＝46.376Km×79.7＝3696.175Km。
天王星の螺旋回転速度＝(3696.175)^1/2Km/s=60.796Km/s。
よって、

天王星は秒速60.796Kmで螺旋回転しながら、太陽の周りを、秒速6.81Kmで公転している。
４．　天王星の表面の1個の原子はどのようになっているか。
螺旋回転の軌道エネルギー＝螺旋回転する物体の表面の原子数×1個の原子が作る電気の光子1個のエネルギーです。
天王星の表面の原子数は6.909×10³⁵個です。
天王星の螺旋回転の軌道エネルギー＝螺旋回転速度²＝60.796²Ｊ＝3696.175J＝天王星の表面の原子数×1個の原子が1公転で作る電気の光子１個のエネルギー。

1個の原子が1公転で作る電気の光子１個のエネルギー＝3.691×10³Ｊ÷(6.909×10³⁵個)＝5.35×10⁻³³Ｊ。
1個の原子で、5.35×10⁻³³Ｊの電気の光子ができる。
電気の光子の軌道＝1.233×10⁻⁴¹Ｊｍ÷電気の光子１個のエネルギー＝1.233×10⁻⁴¹Ｊｍ÷(5.35×10⁻³³Ｊ)＝2.3×10⁻⁹ｍ。
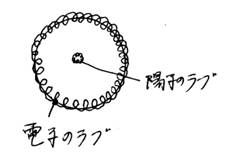
電子のラブの公転軌道は、電気の光子の軌道に等しいから、この電子のラブの公転軌道は、2.3×10⁻⁹ｍです。
５．　天王星の温度はいくらか。
・この場のＡはいくらか。Aは地表の何倍のエネルギーかを示す。
地表の電子のラブの公転軌道÷A＝1.058×10⁻¹⁰ｍ÷Ａ＝2.3×10⁻⁹ｍ。
Ａ＝1.058×10⁻¹⁰ｍ÷(2.3×10⁻⁹ｍ)＝4.6×10⁻²。
・この場の温度はいくらか。温度＝Ａ²＝(4.6×10⁻²)²＝2.116×10⁻³＝0.002116(℃)。
この場の温度は、0.002116℃です。
この温度の値は、天王星が太陽から受ける福射量は、地球を1とすると、0.0027とほぼ等しい。
６．　海王星はどのように螺旋回転しているか。

海王星の公転の軌道エネルギー＝公転速度²＝5.44²Ｊ＝29.594Ｊ

海王星の螺旋回転の軌道エネルギー＝螺旋回転速度²＝公転速度²×79.7＝29.5936Ｊ×79.7＝2358.6Ｊ

螺旋回転速度＝(2358.6)^1/2=48.566Km

海王星の螺旋回転の軌道エネルギー＝螺旋回転速度²＝48.566²Ｊ＝2358.6J

海王星は秒速48.566Kmで螺旋回転(自転)しながら、太陽の周りを、秒速5.44Kmで公転している。

７．　海王星は自転しているのか螺旋回転しているのか。

自転の場合、1自転で進む距離はいくらか。

1周する距離は、2πｒ＝2×π×海王星の半径＝2×3.14×2.4764×10⁴Km＝1.555×10⁵Kmです。

海王星が1自転する周期は、0.671日です。

秒速48.566Kmで0.671日走る距離は、

48.566Km×0.671×24×60×60＝2.816×10⁶Kmです。

これは、1自転の何倍の距離か。

2.816×10⁶Km÷(1.555×10⁵Km)＝1.811×10

1自転の18.11倍の距離です。

よって、海王星は螺旋回転しながら自転している。　

８．　海王星の表面の1個の原子が1公転で作る電気の光子１個のエネルギーはいくらか。

海王星の表面の原子数は6.101×10³⁵個です。

2.359×10³Ｊ÷(6.101×10³⁵個)＝3.867×10⁻³³Ｊ

1個の原子が1公転で作る電気の光子1個のエネルギーは3.867×10⁻³³Ｊです。

・この電子のラブの公転軌道はいくらか。

1.233×10⁻⁴¹Ｊｍ÷(3.867×10⁻³³Ｊ)＝3.189×10⁻⁹ｍ

この電子のラブの公転軌道は、3.189×10⁻⁹ｍです。

・この場のＡはいくらか。

Ａ＝1.058×10⁻¹⁰ｍ÷(3.189×10⁻⁹ｍ)＝3.318×10⁻²

この場のＡは、3.318×10⁻²です。
９．　海王星の温度はいくらか。

温度＝Ａ²＝(3.318×10⁻²)²＝1.1×10⁻³＝0.0011(℃)

この場の温度は、0.0011℃です。

海王星の表面の１原子が作る1個の電気の光子のエネルギーは、3.867×10⁻³³Ｊです。

海王星の表面の電子のラブの公転軌道は、3.189×10⁻⁹ｍで、この場のＡは3.318×10⁻²で、この場の温度は、0.0011℃です。

この値は、海王星が太陽から受ける輻射量は地球を1とすると、0.0011と等しい。

地球を１℃とすると、0.0011℃です。

これをまとめて表に示す。

	公転速度	公転軌道のエネルギー	螺旋軌道のエネルギー	螺旋回転速度	表面の原子数	1原子が1公転で作る電気の光子１個のエネルギー	電子のラブの公転軌道	この場のＡ	この場の温度	太陽より受ける輻射量
天王星	6.81	46.376Ｊ	3696.175Ｊ	60.796Km	6.909×1035個	5.35×10−33Ｊ	2.3×10−9ｍ	4.6×10−2	0.002116℃	0.0021
海王星	5.44	29.594Ｊ	2358.6Ｊ	48.566Km	6.101×1035個	3.867×10−33Ｊ	3.189×10−9ｍ	3.318×10−2	0.0011℃	0.0011

 

この事によって理解できること。

1．太陽から受ける輻射量と同じエネルギーを惑星の表面の原子は作っている。

2．螺旋回転速度²＝螺旋回転の軌道エネルギーの考えは正しい。

3．螺旋回転の軌道エネルギー＝表面の原子数×1原子が1公転で作る電気の光子や磁気の光子のエネルギー