「地球の重力加速度」
(この考えは、2009年9月30日に提出した特願2009−226206に記した。)
1. 重力加速度を計算する時の非合理性。
重力加速度を求めるとき、地球の中心に地球の全ての質量を置き、距離を地球の半径とします。そして、万有引力定数を使って計算します。
地球の重力加速度=地球の質量×1Kgでできる引力×地上の1Kgの物質×1Kgでできる引力÷地球の半径2=地球の質量(Kg)×万有引力定数1/2×1Kg×万有引力定数1/2÷地球の半径2=5.974×1024Kg×(6.672×10−11N/m2/Kg2)1/2×1Kg×(6.672×10−11N/m2/Kg2)1/2÷(6.378×103m)2=5.974×1024Kg×IKg×6.672×10−11N/m2/Kg2÷(6.378×106m)2=9.7983N
この計算の合理的でない点は、次の2点です。
1.地球の中心に地球の全ての質量は存在しない。
2.引力は磁気の光子のエネルギーであり、磁気の光子のエネルギー×自転軌道ではない。
(どのような環境においても、1Kgの質量が作る磁気の光子のエネルギー×自転軌道は6.672×10−11N/m2/Kg2)1/2です。)
しかし、高エネルギーの場で1Kgの質量が作る磁気の光子のエネルギーは、低エネルギーの場で1Kgの質量が作る磁気の光子のエネルギーより大きい。
高エネルギーの場で1Kgの質量が作る引力は、低エネルギーの場で1Kgの質量が作る引力より大きい。引力は場のエネルギーにより異なる。引力となるのは1Kgの質量が作る磁気の光子のエネルギー×自転軌道=(6.672×10−11N/m2/Kg2)1/2、でななく、磁気の光子のエネルギーである引力です。この事については、2009年6月19日に提出した、特願2009−145952.に記した。)
2. 重力加速度は何か。
私は、2008年1月4日に提出した、特願2008−23309.で、加速度=軌道のエネルギー、速度=加速度1/2=軌道のエネルギー1/2、であると理解した。
それで、重力加速度は軌道のエネルギーです。
3. 重力加速度は軌道のエネルギーです。軌道のエネルギーとは何か。
私は、2009年5月11日に提出した、特願2009−114091.で、次のように図解した。
{(図1)太陽が作る惑星の軌道エネルギーの式はどのような事を意味するのか。
軌道のエネルギー=中央のエネルギー×2×105Km÷軌道=太陽の表面の原子数×1原子が作る1個の光子のエネルギー×2×105Km÷軌道=1.325×1037個×10−31J×105Km÷距離=1.325×1011J・Km÷距離
(図2)銀河系の中央のブラックホールの質量が太陽質量の10n倍である場合、ブラックホールが作る星の軌道エネルギーの式はどのような事を意味するのか。
軌道のエネルギー=中央のエネルギー×2×105Km÷軌道=ブラックホールの表面の原子数×1原子が作る1個の光子のエネルギー×2×105Km÷軌道=5.471×1038×102n/3個×10ー25J×2×105Km÷(距離×2)=5.471×1018+2n/3JKm÷距離
(図3)星ができる時、中性子星の質量が太陽質量の10n倍である場合、中性子星が作る軌道エネルギーの式はどのようであるか。どのような事を意味するのか。
軌道のエネルギー=中央のエネルギー×2×105Km÷軌道=中性子星の表面の原子数×1原子が作る1個の光子のエネルギー×2×105Km÷軌道=5.438×1038×102n/3個×2.294×10−26J×105Km÷距離=1.247×1018×102n/3JKm÷距離
(図4)地球が作る月の軌道エネルギーの式はどのようであるか。どのような事を意味するのか。
軌道のエネルギー=中央のエネルギー×2×105Km÷軌道=地球の表面の原子数×1原子が作る1個の光子のエネルギー×2×105Km÷軌道=1.043×1035個×4.444×10−35J ×2×105Km÷(距離×2)=4.635×105J・Km÷距離}
従って、軌道のエネルギーとは、軌道の球体に届く光子のエネルギーの事です。
軌道のエネルギーとは、軌道の球体が受ける光子のエネルギーの事です。
軌道のエネルギーとは、軌道の球体が持つ光子のエネルギーの事です。
重力加速度の軌道のエネルギーは、軌道の球体が持つ光子のエネルギーの事です。
4. 重力加速度の軌道のエネルギーはどのように求められるか。
地表の重力加速度は9.8Jです。地球の中心からの距離は6378Kmです。
それで、軌道の重力加速度の式は、9.8J×6378Km÷地球の中心から軌道までの距離=6.250×104JKm÷地球の中心から軌道までの距離、です。
重力加速度の軌道のエネルギーは、軌道の球体が持つエネルギーの事ですから、地下の軌道の球体が持つエネルギーです。
地下の軌道の球体の表面積に存在する原子の電子のラブが1公転で作る光子のエネルギーです。
5. 重力加速度を作っているのは電気の光子のエネルギーか、それとも、磁気の光子のエネルギーか。
速度を作っているのは電気の光子のエネルギーです。引力を作っているのは磁気の光子のエネルギーです。
太陽から届く電気の光子のエネルギーは、加速度を作ります。加速度1/2の速度を作ります。太陽から届く電気の光子のエネルギーは、惑星の公転速度を作ります。
同時に、太陽から磁気の光子も届きます。この磁気の光子のエネルギーは引力を作ります。
引力の働く方向は、回転する方向に垂直です。(これに関しては、2008年1月4日に提出した、特願2008−23309の「請求項9」に記した。)
重力加速度は、回転する方向に垂直な方向、即ち、地球の中心の方向に働くので、地球の引力になります。引力は、磁気の光子の働きです。
重力加速度を作っているのは磁気の光子のエネルギーです。
また、重力加速度は回転する方向に働き、地球の自転速度を作ります。地球の自転速度を作っているのは電気の光子のエネルギーです。
即ち、重力加速度を作っているのは引力になっている磁気の光子のエネルギーと自転速度になっている電気の光子のエネルギーです。
6. 重力加速度はどのようにできるか。
重力加速度の軌道のエネルギーは、軌道の球体が持つエネルギーの事ですから、地下の軌道の球体が持つ光子のエネルギーです。
地下の軌道の球体の表面積に存在する原子が作る光子のエネルギーです。
それで、重力加速度の軌道のエネルギー=地下の軌道の球体が持つエネルギー=地下の軌道の球体の表面積に存在する原子が作る磁気の光子のエネルギー=地下の軌道の球体の表面積に存在する原子が作る電気の光子のエネルギー=地下の軌道の球体の表面積に存在する原子数×原子の電子のラブが1公転で作る磁気の光子のエネルギー==地下の軌道の球体の表面積に存在する原子数×原子の電子のラブが1公転で作る電気の光子のエネルギー
7. 地球の深さに於ける、重力加速度はいくらか。
重力加速度とは、地球の深さの球体の表面積に存在する原子の電子のラブが1公転で作る光子のエネルギー、です。
即ち、地球の深さの球体の表面積に存在する原子数×その原子の電子のラブが1公転で作る光子のエネルギー、です
地表の重力加速度は9.8Jで、地球の中心からの距離は6378Kmなので、地表の重力加速度は、
地表の重力加速度=9.8J×地球の中心からの距離=9.8J×6378Km=6.250×104JKm、です。
地球の重力加速度の式は、6.250×104JKm÷地球の中心からの距離、です。
地球の深さに於ける重力加速度。
地表は9.8J
地下100Kmの重力加速度=6.250×104JKm÷(6378−100)Km=9.956J
地下500Kmの重力加速度=6.250×104JKm÷(6378−500)Km=10.633J
地下1000Kmの重力加速度=6.250×104JKm÷(6378−1000)Km=11.621J
地下2000Kmの重力加速度=6.250×104JKm÷(6378−2000)Km=14.276J
地下3000Kmの重力加速度=6.250×104JKm÷(6378−3000)Km=18.502J
地下4000Kmの重力加速度=6.250×104JKm÷(6378−4000)Km=26.283J
地下5000Kmの重力加速度=6.250×104JKm÷(6378−5000)Km=45.356J
地下6000Kmの重力加速度=6.250×104JKm÷(6378−6000)Km=165.344J
8. 地下において、原子の電子のラブが1公転で作る磁気の光子のエネルギーはいくらか。この確認。
地球の中の軌道において、熱になる電気の光子の軌道は、2.073×10−5m÷A、です。(この事については、2009年6月19日に提出した、特願2009−145952の「請求項2」に記した。)
・電子のラブが1公転でできる、電気の光子のエネルギーと磁気の光子のエネルギーはいくらか。
電子のラブが1公転でできる、電気の光子のエネルギーと磁気の光子のエネルギー=1.233×10−41Jm÷熱になる電気の光子の軌道=1.233×10−41Jm÷(2.073×10−5m÷A)
地下6000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)=1.233×10−41Jm÷(2.073×10−5m÷60001/2)= 1.233×10−41Jm÷(2.073×10−5m÷77.460)=1.233×10−41Jm÷(2.676×10−7m)=4.608×10−35J
地下5000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷50001/2)= 1.233×10−41Jm÷(2.073×10−5m÷70.711)=1.233×10−41Jm÷(2.932×10−7m)=4.205×10−35J
地下4000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷40001/2)= 1.233×10−41Jm÷(2.073×10−5m÷63.246)=1.233×10−41Jm÷(3.278×10−7m)=3.762×10−35J
地下3000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷30001/2)= 1.233×10−41Jm÷(2.073×10−5m÷54.772)=1.233×10−41Jm÷(3.785×10−7m)=3.258×10−35J
地下2000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷20001/2)= 1.233×10−41Jm÷(2.073×10−5m÷44.721)=1.233×10−41Jm÷(4.636×10−7m)=2.660×10−35J
地下1000Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷10001/2)= 1.233×10−41Jm÷(2.073×10−5m÷31.623)=1.233×10−41Jm÷(6.556×10−7m)=1.881×10−35J
地下500Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷5001/2)= 1.233×10−41Jm÷(2.073×10−5m÷22.361)= 1.233×10−41Jm÷(9.271×10−7m)=1.330×10−35J
地下100Km。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m÷1001/2)= 1.233×10−41Jm÷(2.073×10−5m÷10)= 1.233×10−41Jm÷(2.073×10−6m)=5.948×10−36J
地表。
1.233×10−41Jm÷(2.073×10−5m÷A)= 1.233×10−41Jm÷(2.073×10−5m)=5.948×10−37J
・1秒間で何℃になるか。確認のための計算。
℃=1公転でできる電気の光子のエネルギー×1秒間の公転数÷1℃のJ=1公転でできる電気の光子のエネルギー×(7.96×107)÷(3.769×10−21J)
地下6000Km。4.608×10−35J×(7.96×107)÷(3.769×10−21J)=77.466(℃) 77.4662℃=6000℃
地下5000Km。4.205×10−35J×(7.96×107)÷(3.769×10−21J)=70.691(℃) 70.6912℃=5000℃
地下4000Km。3.762×10−35J×(7.96×107)÷(3.769×10−21J)=63.261(℃) 63.2612℃=4000℃
地下3000Km。3.258×10−35J×(7.96×107)÷(3.769×10−21J)=54.771(℃) 54.7712℃=3000℃
地下2000Km。2.660×10−35J×(7.96×107)÷(3.769×10−21J)=4.472(℃) 4.4722℃=2000℃
地下1000Km。1.881×10−35J×(7.96×107)÷(3.769×10−21J)=31.622(℃) 31.6222℃=1000℃
地下500Km。1.330×10−35J×(7.96×107)÷(3.769×10−21J)=22.359(℃) 22.3592℃=500℃
地下100Km。 5.948×10−36J×(7.96×107)÷(3.769×10−21J)=9.999(℃) 9.9992℃=100℃
地表。 5.948×10−37J×(7.96×107)÷(3.769×10−21J)=1(℃) 12℃=1℃
この事によって、1公転でできる電気の光子のエネルギーは正しい事が確認できた。
9. 地下の、重力加速度を作る軌道の球体の表面積に存在する原子数はいくらか。
地下の重力加速度=地下の軌道の球体の表面積に存在する原子数×1公転でできる磁気の光子のエネルギー=地下の軌道の球体の表面積に存在する原子数×1公転でできる電気の光子のエネルギー
地下の軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる磁気の光子のエネルギー=地下の重力加速度÷1公転でできる電気の光子のエネルギー
地下6000Km。
地下6000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=165.344J÷(4.608×10−35J)=3.588×1036個
地下5000Km。
地下5000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=45.356J÷(4.205×10−35J)=1.079×1036個
地下4000Km。
地下4000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=26.283J÷(3.763×10−35J)=6.985×1035個
地下3000Km。
地下3000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=18.502J÷(3.258×10−35J)=5.679×1035個
地下2000Km。
地下2000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=14.276J÷(2.660×10−35J)=5.367×1035個
地下1000Km。
地下1000Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=11.621J÷(1.881×10−35J)=6.178×1035個
地下500Km。
地下500Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=10.633J÷(1.330×10−35J)=7.767×1035個
地下100Km。
地下100Kmの軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=9.956J÷(5.948×10−36J)=1.674×1036個
地表。
地表の軌道の球体の表面積に存在する原子数=地下の重力加速度÷1公転でできる光子のエネルギー=9.8J÷(5.948×10−37J)=1.648×1037個
この事によって理解できたこと。
1. 地表の重力加速度を作っている球体の表面積に存在する原子数は、1.648×1037個です。ここは、固体ですから緻密に原子が存在する。
2. 地下500Kmから3000Kmまでは、マントルで、軌道の球体の表面積に存在する原子数は約5×1035個から7×1035個です。
地下4000Kmは、外核で液体であるため、原子数は7×1035個です。
地下5000Kmから6000Kmは内核で固体のため、原子数は約1×1036個から4×1036個です。
3. 地下の重力加速度を作っている軌道の球体の表面積に存在する原子数から、地球の中が液体であるか、固体であるかの様子が確認できた。
4. 地下の球体の表面に存在する原子の電子のラブが重力加速度を作っている。
これを表にまとめる。
表1
|
地下の深さ |
重力加速度 |
温度 |
A=温度1/2 |
熱に成る電気の光子の軌道=2.073×10−5m÷A |
1公転でできる熱に成る電気の光子のエネルギー=1公転でできる引力に成る磁気の光子のエネルギー |
重力加速度を作る、地下の球体の表面積に存在する原子数 |
地下の深さの性質 |
地下の深さの性質 |
|
6000Km |
165.34J |
6000℃ |
77.46 |
2.676×10−7m |
4.608×10−35J |
3.588×1036個 |
内核で個体 |
個体 |
|
5000Km |
45.356J |
5000℃ |
70.71 |
2.932×10−7m |
4.205×10−35J |
1.079×1036個 |
内核で個体 |
個体 |
|
4000Km |
26.283J |
4000℃ |
63.25 |
3.278×10−7m |
3.762×10−35J |
6.985×1035個 |
外核で液体 |
液体 |
|
3000Km |
18.502J |
3000℃ |
54.77 |
3.785×10−7m |
3.258×10−35J |
5.679×1035個 |
外核とマントル |
液体 |
|
2000Km |
14.276J |
2000℃ |
44.72 |
4.636×10−7m |
2.660×10−35J |
5.367×1035個 |
マントル |
液体 |
|
1000Km |
11.621J |
1000℃ |
31.623 |
6.556×10−7m |
1.881×10−35J |
6.178×1035個 |
マントル |
液体 |
|
500Km |
10.633J |
500℃ |
22.361 |
9.271×10−7m |
1.330×10−35J |
7.767×1035個 |
マントル |
液体と固体 |
|
100Km |
10.633J |
100℃ |
10 |
2.073×10−6m |
5.948×10−36J |
1.674×1035個 |
マントル |
個体 |
|
地表 |
9.8J |
1℃ |
1 |
2.073×10−5m |
5.948×10−37J |
1.648×1035個 |
地殻 |
個体 |
10. 地球の内核の地下6000Kmは6000℃で、地下5000Kmは5000℃であるのに固体であるのはどのように証明できるか。
・地下6000Kmの軌道の球体の表面積に存在する原子数は3.588×1036個です。この場が固体であるのはどのように証明できるか。
すずの凝固点は、505K−273K=232℃、です。
亜鉛の凝固点は、692K−273K=419℃、です。
アルミニュウムの凝固点は、933K−273K=660℃、です。
銀の凝固点は、1235K−273K=962℃、です。
金の凝固点は、1337K−273K=1064℃、です。
銅の凝固点は、1357K−273K=1084℃、です。
1000℃以上では液体です。地下1000Kmは1000℃ですから、液体です。
地下1000Kmの軌道の球体の表面積に存在する原子数は、6.178×1035個で、液体です。
軌道の球体の表面積に存在する原子数が、6.178×1035個で液体ですから、地下1000Kmから4000Kmまでは、液体です。
地下100Kmは、100℃です。金属元素の凝固点は、100℃以上であるので、地下100Kmは固体です。
地下100Kmの軌道の球体の表面積に存在する原子数は、1.674×1036個で、個体です。
軌道の球体の表面積に存在する原子数が、1.674×1036個で個体ですから、地下6000Kmの軌道の球体の表面積に存在する原子数は3.588×1036個ですから、固体です。
・地下5000Km軌道の球体の表面積に存在する原子数は1.079×1036個です。この場が固体であるのはどのように証明できるか。
地下500Kmの温度は、500℃ですから、アルミや銀や金や銅は固体です。
軌道の球体の表面積に存在する原子数が、7.767×1035個以上の場では、重い金属元素は固体です。
それで、地下、5000Kmでは重い金属元素が存在するので、7.767×1035個以上の場では固体です。地下、5000Kmでは、軌道の球体の表面積に存在する原子数は1.079×1036個ですから固体です。
11. 地下の、重力加速度を作る軌道の球体の表面積に存在する原子数が正しいかどうかはどのように証明できるか。
地下の、重力加速度を作る軌道の球体の表面積に存在する原子数が正しいかどうかは、地下の電子のラブの公転軌道から計算した、軌道の球体の表面積に存在する原子数を調べる事によって、証明できる。
・地下の電子のラブの公転軌道から計算した、軌道の球体の表面積に存在する原子数はいくらか。
Aの軌道では、電子のラブの公転軌道は、1.058×10−10m÷Aです。それで、原子の大きさを1.058×10−10m÷Aとします。半径rKmには、r÷(1.058×10−10m÷A)×103個の原子が存在します。私は、元素数では計算できないので原子数で計算しています。半径rKmの球体の表面には、4π(r÷(1.058×10−10m÷A)×103))2個=4π(r×A×0.9452×1010×103)2=4πr2A2×0.8934×1026個=1.122×1027r2A2個、の原子が存在します。
地下6000Km。
地下6000Kmの温度は6000℃です。この軌道のA2=6000=温度です。
地球の中心から378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×3782×6000個=9.619×1035個、の原子が存在します。
地下5000Km。
地下5000Kmの温度は5000℃です。この軌道のA2=5000=温度です。
地球の中心から1378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×13782×5000個=1.065×1037個、の原子が存在します。
地下4000Km。
地下4000Kmの温度は4000℃です。この軌道のA2=4000=温度です。
地球の中心から2378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×23782×4000個=2.538×1037個、の原子が存在します。
地下3000Km。
地下3000Kmの温度は3000℃です。この軌道のA2=3000=温度です。
地球の中心から3378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×33782×3000個=3.841×1037個、の原子が存在します。
地下2000Km。
地下2000Kmの温度は2000℃です。この軌道のA2=2000=温度です。
地球の中心から4378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×43782×2000個=4.301×1037個、の原子が存在します。
地下1000Km
地下1000Kmの温度は1000℃です。この軌道のA2=1000=温度です。
地球の中心から5378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×53782×1000個=3.245×1037個、の原子が存在します。
地下500Km。
地下500Kmの温度は500℃です。この軌道のA2=500=温度です。
地球の中心から5878Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×58782×500個=1.938×1037個、の原子が存在します。
地下100Km。
地下100Kmの温度は100℃です。この軌道のA2=100=温度です。
地球の中心から6278Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×62782×100個=4.422×1036個、の原子が存在します。
地表。
地表の温度は1℃です。この軌道のA2=1=温度です。
地球の中心から6378Kmの軌道の表面積には、1.122×1027r2A2個=1.122×1027×63782×1個=4.564×1034個、の原子が存在します。
比較
表2
|
地下の深さ |
電子のラブの公転軌道から算出した軌道の球体の表面積に存在する原子数=a |
重力加速度から算出した軌道の球体の表面積に存在する原子数=b |
a÷b |
b÷a |
地下の深さの性質 |
|
6000Km |
9.619×1035個 |
3.588×1036個 |
2.681×10−1 |
5.601 |
個体 |
|
5000Km |
1.065×1037個 |
1.079×1036個 |
9.87 |
1.013×10−1 |
個体 |
|
4000Km |
2.538×1037個 |
6.985×1035個 |
36.220 |
2.752×10−2 |
液体 |
|
3000Km |
3.841×1037個 |
5.679×1035個 |
67.635 |
1.479×10−2 |
液体 |
|
2000Km |
4.301×1037個 |
5.367×1035個 |
80.138 |
1.248×10−2 |
液体 |
|
1000Km |
3.245×1037個 |
6.178×1035個 |
52.525 |
1.904×10−2 |
液体 |
|
500Km |
1.938×1037個 |
7.767×1035個 |
24.95 |
4.008×10−2 |
個体と液体 |
|
100Km |
4.422×1036個 |
1.674×1036個 |
2.642 |
3.786×10−1 |
個体 |
|
地表 |
4.564×1034個 |
1.648×1037個 |
2.769×10−3 |
3.611×102 |
個体 |
この事から理解できる事。
1. 固体の場合、重力加速度から算出した軌道の球体の表面積に存在する原子数は、電子のラブの公転軌道から算出した軌道の球体の表面積に存在する原子数の0.1倍から361倍です。
2. 液体の場合、重力加速度から算出した軌道の球体の表面積に存在する原子数は、電子のラブの公転軌道から算出した軌道の球体の表面積に存在する原子数の0.012倍から0.028倍です。
3. 地表では、重力加速度から算出した軌道の球体の表面積に存在する原子数は、電子のラブの公転軌道から算出した軌道の球体の表面積に存在する原子数の361倍です。この事は、地表は山や谷や海があるので、平面の361倍の原子数が重力加速度を作っていると考えられる。
12. 地球の自転速度はどのようにできるか。重力加速度が自転の加速度であり、自転速度になっていると考える場合。
地球の自転加速度=地球の重力加速度=9.8J
地球の自転速度=地球の重力加速度1/2=9.8J1/2=3.120J=3.120Km/s
地球の自転周期は0.9973日です。
・地球は、1自転する時、地球の円周の何倍の距離を走るか。
0.9973日に走った距離÷地球の円周=0.9973×3.120Km/s×24×60×60s÷(2π×6378Km)=6.712(倍)
地球は、1自転する時、地球の円周の6.712倍の距離を走る。
地球の自転速度はどのようになっているか。重力加速度が自転の加速度であり、自転速度になっていると考える場合、地球は、1自転する時、地球の円周の6.712倍の距離を走る。
13. 地球の自転速度はどのようにできるか。地球は1自転する時、地球の円周の距離を走るとする場合。地球の自転速度を作っているものは何か。そのエネルギーは地表の原子が何個でできるエネルギーか。
地球の自転速度を作っているのは、地表の球体の表面積に存在する原子の電子のラブが1公転で作る電気の光子のエネルギーです。
地球の自転速度は、
地球の1週の距離÷1周するのにかかる時間(秒)=2π地球の半径÷(0.9973日×24×60×60秒)=2π×6378Km÷(8.61667×104秒)=0.4648Km/s、です。
加速度は、速度2=(0.4648Km/s)2=0.216Km/s2、です。
・この軌道のエネルギーは、地表の何個の原子によってできたか。地表の電子のラブが1公転で作る電気の光子のエネルギーは、5.948×10−37Jです。
加速度=軌道のエネルギー=0.216J=5.948×10−37J×原子数
原子数=0.216÷(5.948×10−37J)=3.631×1035(個)
地球の自転速度は、0.4648Km/sです。この加速度は、0.216Km/s2です。
地表の原子の電子のラブは1公転で5.948×10−37Jの電気の光子を作ります。この加速度は、地表の球体の表面の原子数が3.631×1035個でできます。3.631×1035個×5.948×10−37J=0.216J
地球の表面に存在する原子数は、1.138×1035個です。(これについては、2008年10月17日に提出した、特願2008−268538.の「請求項11」に記した。)
3.631×1035個と1.138×1035個はやや等しい。
それで、地球の自転とは、駒のように自転軸を中心に1回転する事かもしれない。
14. 輻射量1/2の電気の光子は何個の電気の光子であるか。
この問題は、2009年5月11日に提出した、特願2009−114091.「宇宙12」の「請求項13」の再再考察です。2009年9月19日に提出した、特願2009−218192の「請求項23」においてもこの問題を取り上げた。
「請求項13」では、輻射熱は、波長が2×2.066×10−5mの赤外線であると考えた。
しかし、惑星の場の軌道のエネルギーが異なるので、熱になる電気の光子の軌道とエネルギーは各々異なる。
「請求項23」では、輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー、とし、輻射量1/2のエネルギー=輻射量1/2×1.165×10−31J、として計算した。これは間違いです。輻射量1/2のエネルギー=輻射量1/2×3.769×10−21Jです。それで、これを訂正し、輻射量1/2の電気の光子数を求める。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=輻射量1/2×3.769×10−21J÷電気の光子1個のエネルギー
水星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=6.671/2×3.769×10−21J÷(1.452×10−36J)=2.583×3.769×10−21J÷(1.452×10−36J)=6.705×1015個
金星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=1.911/2×3.769×10−21J÷(7.769×10−37J)=1.382×3.769×10−21J÷(7.769×10−37J)=6.705×1015個
地球の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=3.769×10−21J÷(5.622×10−37J)=6.704×1015個
火星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=0.431/2×3.769×10−21J÷(3.689×10−37J)=0.6557×3.769×10−21J÷(3.689×10−37J)=6.700×1015個
木星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=0.0371/2×3.769×10−21J÷(1.080×10−37J)=0.192×3.769×10−21J÷(1.080×10−37J)=6.713×1015個
土星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=0.0111/2×3.769×10−21J÷(5.888×10−38J)=0.105×3.769×10−21J÷(5.888×10−38J)=6.714×1015個
天王星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=0.00271/2×3.769×10−21J÷(2.925×10−38J)=0.052×3.769×10−21J÷(2.925×10−38J)=6.700×1015個
海王星の場合。
輻射量1/2の電気の光子数=輻射量1/2の電気の光子のエネルギー÷電気の光子1個のエネルギー=0.00111/2×3.769×10−21J÷(1.867×10−38J)=0.033×3.769×10−21J÷(1.867×10−38J)=6.695×1015個
これを表に示す。
表3
|
惑星 |
惑星の表面の1原子の電子のラブが1公転で作る電気の光子のエネルギー=1.743×10−23JKm÷距離=a |
惑星の表面の1原子の電子のラブの公転軌道=1.233×10−41Jm÷電気の光子のエネルギー=1.233×10−41Jm÷a=b |
熱に成る電気の光子の軌道=電子のラブの公転軌道÷(4.824×10−6)=b÷(4.824×10−6)=c |
熱に成る電気の光子1個のエネルギー=1.233×10−41Jm÷熱に成る電気の光子の軌道=1.233×10−41Jm÷c=d |
輻射量1/2のエネルギー=輻射量1/2×3.769×10−21J=e |
輻射量1/2の電気の光子の数=輻射量1/2のエネルギー÷熱に成る電気の光子のエネルギー=e÷d |
|
水星 |
3.010×10−31J |
4.096×10−11m |
8.491×10−6m |
1.452×10−36J |
9.735×10−21J |
6.705×1015個 |
|
金星 |
1.611×10−31J |
7.654×10−11m |
1.587×10−5m |
7.769×10−37J |
5.209×10−21J |
6.705×1015個 |
|
地球 |
1.165×10−31J |
1.058×10−10m |
2.193×10−5m |
5.622×10−37J |
3.769×10−21J |
6.704×1015個 |
|
火星 |
7.648×10−31J |
1.612×10−10m |
3.342×10−5m |
3.689×10−37J |
2.471×10−21J |
6.700×1015個 |
|
木星 |
2.239×10−32J |
5.507×10−10m |
1.142×10−4m |
1.080×10−37J |
7.236×10−22J |
6.713×1015個 |
|
土星 |
1.219×10−32J |
1.011×10−9m |
2.096×10−4m |
5.888×10−38J |
5.654×10−22J |
6.714×1015個 |
|
天王星 |
6.063×10−33J |
2.034×10−9m |
4.216×10−4m |
2.925×10−38J |
1.958×10−22J |
6.695×1015個 |
|
海王星 |
3.870×10−33J |
3.186×10−9m |
6.604×10−4m |
1.867×10−38J |
1.244×10−22J |
6.695×1015個 |
この事によって理解できる事。
1. 地球に到達する輻射量を1としたとき、惑星に到達する輻射量1/2の電気の光子の数は6.7×1015個で一定です。
2. 私は、従来、たどり着く光子のエネルギーと出発した光子のエネルギーについて、電気の光子1個のエネルギーを単位として計算してきた。この考えは正しい。
例えば、たどり着く光子のエネルギー=Km×aJ÷(2×走った距離)。aJ=出発した光子のエネルギーとKについて。(2007年9月28日に提出した、特願2007−279617.「請求項5」)この式は、2004年6月11日に提出した特願2004−202496に記した。
惑星にたどり着く電気の光子1個のエネルギー=太陽を出発する電気の光子1個のエネルギー×見かけ上に換算する定数÷距離、の式を再考する。(2009年5月11日に提出した、特願2009−114091.の「請求項7」)、等です。
【図面の簡単な説明】
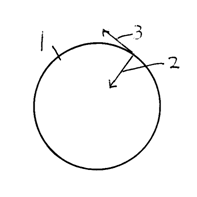
【図1】重力加速度を作っているのは、引力2と成る磁気の光子のエネルギーと、加速度に成っている電気の光子のエネルギーです。
引力=重力加速度1/2=重力加速度の軌道のエネルギー1/2=重力加速度の軌道の磁気の光子のエネルギー1/2
速度=重力加速度1/2=重力加速度の軌道のエネルギー1/2=重力加速度の軌道の電気の光子のエネルギー1/2
地球は大きいので、引力=速度、です。
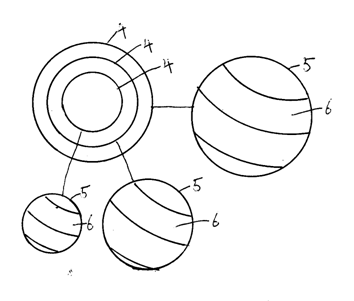
【図2】軌道の重力加速度は、軌道の重力加速度=9.8J×地球の半径÷地球の中心から軌道までの距離=9.8J×6378Km÷地球の中心から軌道までの距離=6.250×104JKm÷地球の中心から軌道までの距離=6.250×104JKm÷(6378−軌道)Km、の式で求められる。
軌道の重力加速度は、軌道の球体の表面積に存在する原子が1公転で作る光子のエネルギーであり、軌道の球体の表面積に存在する原子数×原子の電子のラブが1公転で作る光子のエネルギー、です。
地下の軌道の重力加速度=6.250×104JKm÷地球の中心から軌道までの距離=6.250×104JKm÷(6378−軌道)Km=軌道の球体の表面積に存在する原子が1公転で作る光子のエネルギー=軌道の球体の表面積に存在する原子数×原子の電子のラブが1公転で作る光子のエネルギー
【符号の説明】
1 地球
2 引力=重力
3 速度
4 軌道
5 軌道の球体
6 軌道の重力加速度=軌道の球体の表面積に存在する原子数×1原子の電子のラブが1公転で作る光子のエネルギー
【図面】
【図1】
【図2】