![]()
�u���ԂƋ�ԂƋO���ƃG�l���M�[�ƈ��́v
�P�D��Ԃ̒Z�k�Ɗg��̌����Ǝ��Ԃ̒Z�k�Ɗg��̌����Ǝ��ԂƋ�Ԃ̒Z�k�Ɗg��̌����ɂ��āB
���́A�d�q�Ɨz�q�̒��ɒ������q�����݂���B���̖���d�q�̃��u�Ɨz�q�̃��u�Ɩ��t�����B�d�q�̃��u�̎��ʂ�9.1095�~10�|31Kg�ŁA���]���Ȃ�����]���Ă���B�z�q�̃��u�̎��ʂ�1.67265�~10�|27Kg�ŁA���]���Ȃ�����]���Ă���B
�n�\�̓d�q�̃��u�̌��]�O����1.058�~10�|10���Ƃ��A�G�l���M�[��8.187�~10�|14J�Ƃ��A���x��1���Ƃ���B
�n�\�̃G�l���M�[�̉��{�̃G�l���M�[�����������AA�{�̃G�l���M�[�Ƃ���B
����̃G�l���M�[��A�{�̏ꍇ�A�d�q�̃��u�̌��]�O����1.058�~10�|10����A�ł��B
���̓d�q�̃��u�̌��]�O�����������Ȃ鎖�ɂ��A��Ԃ�1/A�ɒZ�k����B
�����̓d�q�̃��u�̌��]�O�����������Ȃ鎖�ɂ��A1�b�Ԃɑ��鋗���͏������Ȃ�A�b���͒Z�k���A���Ԃ�1/A�ɒZ�k����B
����̃G�l���M�[��A�{�̏ꍇ�A�d�q�̃��u�̃G�l���M�[�͑傫���Ȃ�A���͂͑傫���Ȃ�B���̎��ɂ���āA����͒Z�k����B
����Ԃ̒Z�k�Ɗg��̌���
�d�q�̃��u�̌��]�O�����������Ȃ�قNj�Ԃ͒Z�k����B
���G�l���M�[�̏�قǁA�d�q�̃��u�̌��]�O���͏������Ȃ�A��Ԃ͒Z�k����B
��G�l���M�[�̏�قǁA�d�q�̃��u�̌��]�O���͑傫���Ȃ�A��Ԃ͊g�傷��B
�����Ԃ̒Z�k�Ɗg��̌���
�d�q�̃��u�̌��]�O�����������Ȃ�قǕb���͏������Ȃ�A���Ԃ͒Z�k����B
���G�l���M�[�̏�قǁA�d�q�̃��u�̕b���͏������Ȃ�A���Ԃ͒Z�k���Ă���B
��G�l���M�[�̏�قǁA�d�q�̃��u�̕b���͑傫���Ȃ�A���Ԃ͊g�債�Ă���B
�����ԂƋ�Ԃ̒Z�k�Ɗg��̌���
���G�l���M�[�̏�قǁA�����ł���A���͂͑傫���A��ԂƎ��Ԃ͒Z�k���Ă���B
��G�l���M�[�̏�قǁA�ቷ�ł���A���͂͏������A��ԂƎ��Ԃ͊g�債�Ă���B
�Q�D�@���G�l���M�[�̏�̋�ԂƎ��Ԃ̒Z�k�ɂ��āB
���G�l���M�[�̏�̈�ʎ���\�Ɏ����B
���G�l���M�[�̏�̃G�l���M�[��n�\��A�{�Ƃ���B
|
��̉��x |
�n�\�@1�� |
A2�� |
���G�l���M�[�̏� |
|
���A |
1 |
A |
|
|
�d�q�̃��u�̌��]�O�� |
1.058�~10�|10�� |
�n�\�̓d�q�̃��u�̌��]�O����A=1.058�~10�|10����A |
�d�q�̃��u�̌��]�O���͏������Ȃ�̂ŁA��Ԃ͒Z�k���� |
|
�d�q�̃��u�̃G�l���M�[ |
8.190�~10�|14J |
�n�\�̓d�q�̃��u�̃G�l���M�[�~A=8.665�~10�|24�i����(1.058�~10�|10����A)��8.190�~10�|14J�~A |
�d�q�̃��u�̃G�l���M�[�͑傫���Ȃ�̂ŁA���͂͑傫���Ȃ�A���ԂƋ�Ԃ͒Z�k���� |
|
�d�q�̃��u�̕b�� |
2.1�~106�� |
�n�\�̓d�q�̃��u�̕b����A=2.1�~106����A |
�d�q�̃��u�̕b���͏������Ȃ�̂Ŏ��Ԃ͒Z�k���� |
|
�d�q�̃��u��1�b�Ԃɍ����͂ƂȂ鎥�C�̌��q�̃G�l���M�[ |
3.769�~10�|21J |
1.233�~10�|41Jm��(�n��ŔM�ɂȂ�O����A)�~(7.96�~107)2��3.769�~10�|21J�~A |
�d�q�̃��u��1�b�Ԃɍ����͂ƂȂ鎥�C�̌��q�̃G�l���M�[�͑傫���Ȃ�̂ŁA���ԂƋ�Ԃ͒Z�k���� |
�R�D�@�n���̒n���̏ꍇ
�E�n��6500Km�̉��x��7327���ł��B���x1/2=85.6���@�@A=85.6
��Ԃ͌��]�O���Ŕ�r����B���Ԃ͕b���Ŕ�r����B
�d�q�̃��u�̌��]�O���́A1.058�~10�|10����85.6�ŁA�n�\��85.6����1�ł��B
1��85.6��1.16�~10�|2
��Ԃ͒n�\���P�Ƃ���ƁA1.16�~10�|2�ɒZ�k���Ă��܂��B
�b���́A3.14�~1.058�~10�|10����85.6�~�i7.96�~107)2���]��2.459�~104���ŁA�n�\��85.6����1�ł��B
1��85.6��1.16�~10�|2
���Ԃ͒n�\���P�Ƃ���ƁA1.16�~10�|2�ɒZ�k���Ă��܂��B
�\�ɂ��������܂��B
|
�n�� |
���x |
A�����x1/2 |
�d�q�̃��u�̌��]�O�� |
��� (�n�\��1�Ƃ���) |
�b�� (�n�\��1�Ƃ���) |
���� (�n�\��1�Ƃ���) |
|
6500Km |
7327�� |
85.6 |
�n�\��85.6����1 |
1.16�~10�|2 |
1.16�~10�|2 |
1.16�~10�|2 |
|
6000Km |
6000�� |
77.46 |
�n�\��77.46����1 |
1.29�~10�|2 |
1.29�~10�|2 |
1.29�~10�|2 |
|
5000Km |
5000�� |
70.71 |
�n�\��70.71����1 |
1.414�~10�|2 |
1.414�~10�|2 |
1.414�~10�|2 |
|
4000Km |
4000�� |
63.25 |
�n�\��63.25����1 |
1.581�~10�|2 |
1.581�~10�|2 |
1.581�~10�|2 |
|
3000Km |
3000�� |
54.77 |
�n�\��54.77����1 |
1.826�~10�|2 |
1.826�~10�|2 |
1.826�~10�|2 |
|
2000Km |
2000�� |
44.72 |
�n�\��44.72����1 |
2.236�~10�|2 |
2.236�~10�|2 |
2.236�~10�|2 |
|
1000Km |
1000�� |
31.62 |
�n�\��31.62����1 |
3.162�~10�|2 |
3.162�~10�|2 |
3.162�~10�|2 |
�S�D�@���z�̒��̏ꍇ
�E�[��7�~105Km�̉��x�́A15�~106���ł��B���x1/2=3.873�~103���@A=3.873�~103
�d�q�̃��u�̌��]�O���́A�n�\��3.873�~103����1�ł��B
��Ԃ͒n�\���P�Ƃ���ƁA2.582�~10�|4�ɒZ�k���Ă��܂��B
�b���́A�n�\��3.873�~103����1�ł��B
1���i3.873�~103�j��2.582�~10�|4
���Ԃ͒n�\���P�Ƃ���ƁA2.582�~10�|4�ɒZ�k���Ă��܂��B
�\�Ɏ����B
|
���z�̐[�� |
���x |
A�����x1/2 |
�d�q�̃��u�̌��]�O�� |
��� (�n�\��1�Ƃ���) |
�b�� (�n�\��1�Ƃ���) |
���� (�n�\��1�Ƃ���) |
|
7�~105Km |
15�~106�� |
3.873�~103�@ |
�n�\��3.873�~103����1 |
2.582�~10�|4 |
2.582�~10�|4 |
2.582�~10�|4 |
|
6�~105Km |
15�~106�� |
3.873�~103 |
�n�\��3.873�~103����1 |
2.582�~10�|4 |
2.582�~10�|4 |
2.582�~10�|4 |
|
5�~105Km |
11.7�~106�� |
3.428�~103 |
�n�\��3.428�~103����1 |
2.917�~10�|4 |
2.917�~10�|4 |
2.917�~10�|4 |
|
4�~105Km |
8.5�~106�� |
2.915�~103 |
�n�\��2.915�~103����1 |
3.431�~10�|4 |
3.431�~10�|4 |
3.431�~10�|4 |
|
3�~105Km |
5.25�~106�� |
2.291�~103 |
�n�\��2.291�~103����1 |
4.365�~10�|4 |
4.365�~10�|4 |
4.365�~10�|4 |
|
2�~105Km |
2�~106�� |
1.414�~103 |
�n�\��1.414�~103����1 |
7.072�~10�|4 |
7.072�~10�|4 |
7.072�~10�|4 |
|
105Km |
106�� |
103 |
�n�\��103����1 |
10�|3 |
10�|3 |
10�|3 |
|
104Km |
105�� |
3.162�~102 |
�n�\��3.162�~102����1 |
3.163�~10�|3 |
3.163�~10�|3 |
3.163�~10�|3 |
|
103Km |
104�� |
102 |
�n�\��102����1 |
10�|2 |
10�|2 |
10�|2 |
|
4�~102Km |
6.4�~103�� |
80 |
�n�\��80����1 |
1.25�~10�|2 |
1.25�~10�|2 |
1.25�~10�|2 |
|
�PKm |
4.3�~103�� |
65.574 |
�n�\��65.574����1 |
1.525�~10�|2 |
1.525�~10�|2 |
1.525�~10�|2 |
�T�D�@�u���b�N�z�[���̏ꍇ
�u���b�N�z�[���̉��x��1.5�~1010���Ƃ��܂��ƁA���x1/2=1.225�~105���@A=1.225�~105
�u���b�N�z�[���̎��ԂƋ�Ԃ́A�n�\��1.225�~105����1�ł��B
1���i1.225�~105�j��8.163�~10�|6
���Ԃ͒n�\���P�Ƃ���ƁA8.163�~10�|6�ɒZ�k���Ă��܂��B
��Ԃ͒n�\���P�Ƃ���ƁA8.163�~10�|6�ɒZ�k���Ă��܂��B
�U�D�@�F���̏�ɂ����āA�d�q�̃��u�̃G�l���M�[�Ɠd�q�̃��u�̋O����A�i�n�\��1�Ƃ���G�l���M�[�̔�j�Ƌ�ԂƎ��ԂƉ��x�ƈ��͂�\�ɂ���Ƃǂ̂悤�ł��邩�B
�����u�̋O���G�l���M�[��8.665�~10�|24Jm�@�ł��B(�n�\�̏ꍇ�A�d�q�̃��u�̌��]�O���~�d�q�̃��u�̃G�l���M�[��1.058�~10�|10���~8.190�~10�|14J��8.665�~10�|24Jm)
���F���̓d�q�̋O���G�l���M�[�����̎��ɂ���ĕ\���ł���B
���F���̓d�q�̃��u�̋O���ƃG�l���M�[����A�n�\��1�Ƃ���A�G�l���M�[�̔�Ƌ�Ԃ̔�Ǝ��Ԃ̔�Ɖ��x�̔�ƈ��͂̔䂪�����ł���B
������A�\�ɂ���B
|
�d�q�̃��u�̃G�l���M�[ 8.665�~ |
�d�q�̃��u�̌��]�O�� |
A���n�\��1�Ƃ���G�l���M�[�̔� |
��ԁi�n�\���P�Ƃ���j |
���ԁi�n�\���P�Ƃ���j |
���x�i�n�\���P�Ƃ���j |
���́i�n�\���P�Ƃ���j |
|
100J |
10�|24�� |
1014 |
10�|14 |
10�|14 |
1028�� |
1028�{ |
|
10�|1J |
10�|23�� |
1013 |
10�|13 |
10�|13 |
1026�� |
1026�{ |
|
10�|2J |
10�|22�� |
1012 |
10�|12 |
10�|12 |
1024�� |
1024�{ |
|
10�|3J |
10�|21�� |
1011 |
10�|11 |
10�|11 |
1022�� |
1022�{ |
|
10�|4J |
10�|20�� |
1010 |
10�|10 |
10�|10 |
1020�� |
1020�{ |
|
10�|5J |
10�|19�� |
109 |
10�|9 |
10�|9 |
1018�� |
1018�{ |
|
10�|6J |
10�|18�� |
108 |
10�|8 |
10�|8 |
1016�� |
1016�{ |
|
10�|7J |
10�|17�� |
107 |
10�|7 |
10�|7 |
1014�� |
1014�{ |
|
10�|8J |
10�|16�� |
106 |
10�|6 |
10�|6 |
1012�� |
1012�{ |
|
10�|9J |
10�|15�� |
105 |
10�|5 |
10�|5 |
1010�� |
1010�{ |
|
10�|10J |
10�|14�� |
104 |
10�|4 |
10�|4 |
108�� |
108�{ |
|
10�|11J |
10�|13�� |
103 |
10�|3 |
10�|3 |
106�� |
106�{ |
|
10�|12J |
10�|12�� |
102 |
10�|2 |
10�|2 |
104�� |
104�{ |
|
10�|13J |
10�|11�� |
10 |
10�|1 |
10�|1 |
102�� |
102�{ |
|
10�|14J |
10�|10�� |
�P(�n�\) |
�P |
�P |
1�� |
�P |
|
10�|15J |
10�|9�� |
10�|1 |
10 |
10 |
10�|2�� |
10�|2�{ |
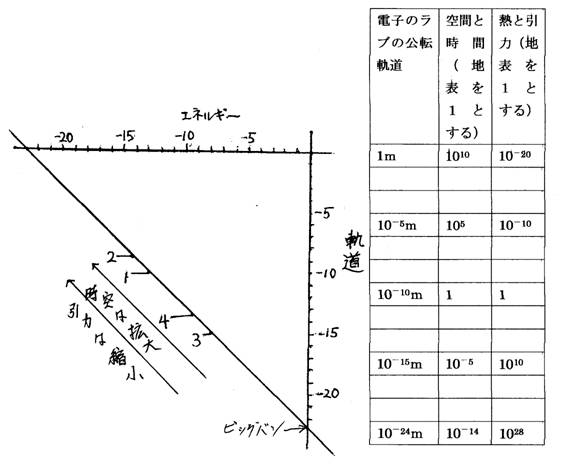
�V�D�F���̏�ɂ����āA�G�l���M�[�ƋO���̊W�͂ǂ̂悤�ȃO���t�Ō�����邩�B
���u�̃G�l���M�[�~�O����8.665�~10�|24Jm�ł��B
���u�̃G�l���M�[��10��J�Ƃ��A���u�̌��]�O����10�����Ƃ���B�ΐ����O���t�ɂ���B
10��J�~10������8.665�~10�|24Jm
���{�����|24+log8.665=�|24�{0.931
���{�����|23
�����|���|23
���u�̃G�l���M�[��10��J�Ƃ��A���u�̌��]�O����10�����Ƃ���ƁA���̊W�̃O���t�́A�����|���|23�ł��B
���F���̃G�l���M�[�ƋO���̊W�̃O���t�ʼn��������ł��邩�B
�@���̏�̃G�l���M�[���A�F���̂ǂ̓_�ɑ�����̂��𗝉��ł���B
�A����0�̎��A�r�b�O�o�����������Ɛ��@�ł���B
�B�r�b�O�o�����������ȑO�̉F�����L�鎖���\�z�ł���B���̉F���́A�G�l���M�[��8.665J���傫���B���]�O����10�|24����菬�����B
�y�����̐����z
�P�@�n�\�̓d�q�̃��u�́A���]�O����1.058�~10�|10���ŁA�G�l���M�[��8.187�~10�|14J�ł�����A�����|10�ŁA�����|14�{0.91���|13�ł��B
�Q�@�d�q�̕���́A�|273���ł�����A���̏�̓d�q�̃��u�̌��]�O���́A1.058�~10�|10���~(273)1/2��1.058�~10�|10���~16.522��1.748�~10�|9���ł��B
����ŁA�����|9+log1.748=�|9�{0.24���|8.76�@�ŁA�����|23�{8.76��14.24 �@�ł��B
�R�@�u���b�N�z�[���̓d�q�̃��u�̌��]�O���́A1.058�~10�|10����(1.5�~1010��)1/2=1.058�~10�|10����(1.225�~105)��8.637�~10�|16���ł��B
����ŁA�����|16�{log8.637=�|16�{0.94���|15�ŁA�����|8�ł��B
�S�@���z�̒��S�́A�d�q�̃��u�̌��]�O���́A1.058�~10�|10����(1.5�~107��)1/2��1.058�~10�|10�����i3.873�~103�j��2.732�~10�|14���ł��B
����ŁA�����|14�{log2.732=�|14�{0.436���|13.56�ŁA�����|23�{13.56���|9.44
�W�D�@�F���̏�ɂ������ԂƎ��Ԃ̊g��ƈ��͂̊W�͂ǂ̂悤�ł��邩�B
�F���̏�ɂ�����A�G�l���M�[�ƋO���̊W�̃O���t�ɂ��A�d�q�̃��u�̌��]�O�����傫���Ȃ�A�G�l���M�[���������Ȃ�ɏ]���āA��ԂƎ��Ԃ͊g�傷��B���͂͏k������B