「宇宙の軌道エネルギー」
(この考えは、2011年5月22日に提出した特願2011−114246に記した。)
1. 宇宙はどのように回転しているか。
宇宙の状態は筒型である。この事は、宇宙は螺旋回転をしている事を示す。
2. 宇宙の筒型の螺旋回転を縦にカットすると、そこには何が現れるか。
宇宙の筒の螺旋回転を縦にカットすると、そこには、公転の軌道が現れる。
3. 宇宙の公転が一定の範囲で行われている。これはどうしてか。
宇宙の公転が一定の範囲で行われていることは、中央に強い引力がはたらいている事を示す。その引力は変わらない状態で、長時間続いている事を示す。
4. 宇宙の公転軌道エネルギーの式を求める。
筒型の中で螺旋回転を行わせている、筒の中央のブラックホールの質量はいくらか。
筒を輪切りにすると、公転軌道が現れる。この中央に存在するブラックホールの質量を10n太陽質量とする。
宇宙の公転速度2=5.4×1018+2n/3JKm÷距離。宇宙の公転速度2×距離=5.4×1018+2n/3JKm
宇宙の公転速度と距離を知る事によって、宇宙の公転軌道エネルギーの式を求めることができる。
それで、次の事象から宇宙の公転速度を秒速600Kmとする。
{現在、局部超銀河団はうみへび座からケンタウルス座方向に向かって秒速600Kmで引き寄せられている事が解っています。
ペルセウス座超銀河団やうみへび座超銀河団、ケンタウルス座超銀河団なども同じ方向に引き寄せられている事がわかり、この方向の約2億光年かなたに何か巨大な引力原があると推測されました。}(140億光年のすべてが見えてくる宇宙の辞典より)
筒の半径を1億光年とし、軌道の速度を秒速600Kmとする。秒速が600Kmである軌道が、a半径107光年、b半径2×107光年、c半径3×107光年、d半径4×107光年、e半径5×107光年であると仮定し、それぞれの場合の宇宙の軌道エネルギーの式を求める。
a. 半径107光年の軌道の秒速が600Kmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=(6×102)2×107×9.46×1012Km=3.406×1025JKm
宇宙の公転軌道エネルギー=3.406×1025JKm÷距離、です。
b. 半径2×107光年の軌道の秒速が600Kmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=(6×102)2×2×107×9.46×1012Km=6.811×1025JKm
宇宙の公転軌道エネルギー=6.811×1025JKm÷距離、です。
c. 半径3×107光年の軌道の秒速が600Kmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=(6×102)2×3×107×9.46×1012Km=1.022×1026JKm
宇宙の公転軌道エネルギー=1.022×1026JKm÷距離、です。
d. 半径4×107光年の軌道の秒速が600Kmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=(6×102)2×4×107×9.46×1012Km=1.362×1026JKm
宇宙の公転軌道エネルギー=1.362×1026JKm÷距離、です。
e. 半径5×107光年の軌道の秒速が600Kmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=(6×102)2×5×107×9.46×1012Km=1.703×1026JKm
宇宙の公転軌道エネルギー=1.703×1026JKm÷距離、です。
表1
|
|
a |
b |
c |
d |
e |
|
半径 |
107光年 |
2×107光年 |
3×107光年 |
4×107光年 |
5×107光年 |
|
速度 |
600Km |
600Km |
600Km |
600Km |
600Km |
|
宇宙の公転軌道エネルギー |
3.406×1025 Km÷距離 |
6.811×1025 Km÷距離 |
1.022 ×1026 JKm÷距離 |
1.362×1026 JKm÷距離 |
1.703×1026 JKm÷距離 |
5. 各々の場合、宇宙の公転軌道における公転速度はいくらか。
aの場合。宇宙の公転軌道エネルギー=3.406×1025JKm÷距離、です。
107光年の軌道では、速度2=3.406×1025JKm÷(107×9.46×1012Km)=3.600×105
公転速度=(3.600×105)1/2=6×102Km/s、です。
2×107光年の軌道では、速度2=3.406×1025JKm÷(2×107×9.46×1012Km)=1.800×105
公転速度=(1.800×105)1/2=4.243×102 Km/s、です。
3×107光年の軌道では、速度2=3.406×1025JKm÷(3×107×9.46×1012Km)=1.200×105
公転速度=(1.200×105)1/2=3.464×102 Km/s、です。
4×107光年の軌道では、速度2=3.406×1025JKm÷(4×107×9.46×1012Km)=9.001×104
公転速度=(9.001×104)1/2=3.000×102 Km/s、です。
5×107光年の軌道では、速度2=3.406×1025JKm÷(5×107×9.46×1012Km)=7.201×104
公転速度=(7.201×104)1/2=2.683×102 Km/s、です。
cの場合。宇宙の公転軌道エネルギー=1.022×1026JKm÷距離、です。
107光年の軌道では、速度2=1.022×1026JKm÷(107×9.46×1012Km)=1.080×106
公転速度=(1.080×106)1/2=1.039×103 Km/s、です。
2×107光年の軌道では、速度2=1.022×1026JKm÷(2×107×9.46×1012Km)=5.402×105
公転速度=(5.402×105)1/2=7.350×102Km/s、です。
3×107光年の軌道では、速度2=1.022×1026JKm÷(3×107×9.46×1012Km)=3.601×105
公転速度=(3.601×105)1/2=6.001×102 Km/s、です。
4×107光年の軌道では、速度2=1.022×1026JKm÷(4×107×9.46×1012Km)=2.701×105
公転速度=(2.701×105)1/2=5.197×102 Km/s、です。
5×107光年の軌道では、速度2=1.022×1026JKm÷(5×107×9.46×1012Km)=2.161×105
公転速度=(2.161×105)1/2=4.649×102 Km/s、です。
eの場合。宇宙の公転軌道エネルギー=1.703×1026JKm÷距離、です。
107光年の軌道では、速度2=1.703×1026JKm÷(107×9.46×1012Km)=1.800×106
公転速度=(1.800×106)1/2=1.342×103 Km/s、です。
2×107光年の軌道では、速度2=1.703×1026JKm÷(2×107×9.46×1012Km)=9.001×105
公転速度=(9.001×105)1/2=9.487×102Km/s、です。
3×107光年の軌道では、速度2=1.703×1026JKm÷(3×107×9.46×1012Km)=6.001×105
公転速度=(6.001×105)1/2=7.747×102 Km/s、です。
4×107光年の軌道では、速度2=1.703×1026JKm÷(4×107×9.46×1012Km)=4.501×105
公転速度=(4.501×105)1/2=6.709×102 Km/s、です。
5×107光年の軌道では、速度2=1.703×1026JKm÷(5×107×9.46×1012Km)=3.600×105
公転速度=(3.600×105)1/2=6×102Km/s、です。
6. 各々の場合、宇宙の公転軌道は1公転するのに何年かかるか。現在まで何周しているか。
1周するのにかかる年数=円周÷1年間に走る距離=2×3.14×半径(光年)×9.46×1012Km÷(秒速Km/s×365×24×60×60s)=1.883×106×半径(光年)÷秒速
aの場合。
107光年の軌道を公転する。公転速度=6×102Km/s、です。
1周するのにかかる年数=2×3.14×107×9.46×1012Km÷(6×102Km/s×365×24×60×60s)=5.941×1020÷(1.892×1010)=3.140×1010(年)
何周しているか。
137×108年÷(3.140×1010年)=0.436回転
2×107光年の軌道を公転する。公転速度=4.243×102 Km/s、です。
1周するのにかかる年数=2×3.14×2×107×9.46×1012Km÷(4.243×102Km/s×365×24×60×60s)=1.188×1021÷(1.338×1010)=8.879×1010(年)
何周しているか。
137×108年÷(8.879×1010年)=0.154回転
3×107光年の軌道を公転する。公転速度=3.464×102 Km/s、です。
1周するのにかかる年数=2×3.14×3×107×9.46×1012Km÷(3.464×102Km/s×365×24×60×60s)=1.782×1021÷(1.092×1010)=1.632×1011(年)
何周しているか。
137×108年÷(1.632×1011年)=0.084回転
4×107光年の軌道を公転する。公転速度=3.000×102 Km/s、です。
1周するのにかかる年数=2×3.14×4×107×9.46×1012Km÷(3.000×102Km/s×365×24×60×60s)=2.376×1021÷(9.461×109)=2.511×1011(年)
何周しているか。
137×108年÷(2.511×1011年)=0.055回転
5×107光年の軌道を公転する。公転速度=2.683×102 Km/s、です。
1周するのにかかる年数=2×3.14×5×107×9.46×1012Km÷(2.683×102Km/s×365×24×60×60s)=2.970×1021÷(8.461×109)=3.510×1011(年)
何周しているか。
137×108年÷(3.510×1011年)=0.039回転
cの場合。
107光年の軌道を公転する。公転速度=1.039×103 Km/s、です。
1周するのにかかる年数=2×3.14×107×9.46×1012Km÷(1.039×103Km/s×365×24×60×60s)=5.941×1020÷(3.277×1010)=1.813×1010(年)
何周しているか。
137×108年÷(1.813×1010年)=0.756回転
2×107光年の軌道を公転する。公転速度=7.350×102Km/s、です。
1周するのにかかる年数=2×3.14×2×107×9.46×1012Km÷(7.350×102Km/s×365×24×60×60s)=1.188×1021÷(2.318×1010)=5.125×1010(年)
何周しているか。
137×108年÷(5.125×1010年)=0.267回転
3×107光年の軌道を公転する。公転速度=6.001×102 Km/s、です。
1周するのにかかる年数=2×3.14×3×107×9.46×1012Km÷(6.001×102Km/s×365×24×60×60s)=1.782×1021÷(1.892×1010)=9.419×1010(年)
何周しているか。
137×108年÷(9.419×1010年)=0.145回転
4×107光年の軌道を公転する。公転速度=5.197×102 Km/s、です。
1周するのにかかる年数=2×3.14×4×107×9.46×1012Km÷(5.197×102Km/s×365×24×60×60s)=2.376×1021÷(1.639×1010)=1.450×1011(年)
何周しているか。
137×108年÷(1.450×1011年)=0.094回転
5×107光年の軌道を公転する。公転速度=4.649×102 Km/s、です。
1周するのにかかる年数=2×3.14×5×107×9.46×1012Km÷(4.649×102Km/s×365×24×60×60s)=2.970×1021÷(1.466×1010)=2.026×1011(年)
何周しているか。
137×108年÷(2.026×1011年)=0.068回転
eの場合。
107光年の軌道を公転する。公転速度=1.342×103 Km/s、です。
1周するのにかかる年数=2×3.14×107×9.46×1012Km÷(1.342×103Km/s×365×24×60×60s)=5.941×1020÷(4.232×1010)=1.404×1010(年)
何周しているか。
137×108年÷(1.404×1010年)=0.9758回転
2×107光年の軌道を公転する。公転速度=9.487×102Km/s、です。
1周するのにかかる年数=2×3.14×2×107×9.46×1012Km÷(9.487×102Km/s×365×24×60×60s)=1.188×1021÷(2.992×1010)=3.971×1010(年)
何周しているか。
137×108年÷(3.971×1010年)=0.345回転
3×107光年の軌道を公転する。公転速度=7.747×102 Km/s、です。
1周するのにかかる年数=2×3.14×3×107×9.46×1012Km÷(7.747×102Km/s×365×24×60×60s)=1.782×1021÷(2.443×1010)=7.294×1010(年)
何周しているか。
137×108年÷(7.294×1010年)=0.188回転
4×107光年の軌道を公転する。公転速度=6.709×102 Km/s、です。
1周するのにかかる年数=2×3.14×4×107×9.46×1012Km÷(6.709×102Km/s×365×24×60×60s)=2.376×1021÷(2.116×1010)=1.123×1011(年)
何周しているか。
137×108年÷(1.123×1011年)=0.122回転
5×107光年の軌道を公転する。
1周するのにかかる年数=2×3.14×5×107×9.46×1012Km÷(6×102Km/s×365×24×60×60s)=2.970×1021÷(1.892×1010)=1.570×1011(年)
何周しているか。
137×108年÷(1.570×1011年)=0.087回転
表2
|
|
a |
c |
e |
|
宇宙の公転軌道エネルギー |
3.406×1025JKm |
1.022×1026JKm |
1.703×1026JKm |
|
公転速度 |
|
|
|
|
107光年 |
6×102Km/s |
1.039×103Km/s |
1.342×103Km/s |
|
2×107光年 |
4.243×102Km/s |
7.350×102Km/s |
9.487×102Km/s |
|
3×107光年 |
3.464×102Km/s |
6×102Km/s |
7.747×102Km/s |
|
4×107光年 |
3.000×102Km/s |
5.197×102Km/s |
6.709×102Km/s |
|
5×107光年 |
2.683×102Km/s |
4.649×102Km/s |
6×102Km/s |
|
1周するにかかる年数 |
|
|
|
|
107光年 |
3.140×1010(年) |
1.813×1010(年) |
1.404×1010(年) |
|
2×107光年 |
8.879×1010(年) |
5.125×1010(年) |
3.971×1010(年) |
|
3×107光年 |
1.632×1011(年) |
9.419×1010(年) |
7.294×1010(年) |
|
4×107光年 |
2.511×1011(年) |
1.450×1011(年) |
1.123×1011(年) |
|
5×107光年 |
3.510×1011(年) |
2.026×1011(年) |
1.570×1011(年) |
|
何周しているか |
|
|
|
|
107光年 |
0.436回転 |
0.756回転 |
0.9758回転 |
|
2×107光年 |
0.154回転 |
0.267回転 |
0.345回転 |
|
3×107光年 |
0.084回転 |
0.145回転 |
0.188回転 |
|
4×107光年 |
0.055回転 |
0.094回転 |
0.122回転 |
|
5×107光年 |
0.039回転 |
0.068回転 |
0.087回転 |
7. 宇宙の公転軌道エネルギーの式はどのようであるか。公転速度はいくらか。宇宙の公転軌道は1公転するのに何年かかるか。現在まで何周しているか。一般式を求める。
・宇宙の公転軌道エネルギーの式はどのようであるか。一般式を求める。
a. 半径107光年の軌道の秒速がDKmである場合。
宇宙の公転軌道エネルギー=D2×中心からの距離=D2×107×9.46×1012Km=D2×9.46×1019
JKm
宇宙の公転軌道エネルギー=D2×9.46×1019JKm÷距離、です。
b. 半径2×107光年の軌道の秒速がDKmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=D2×2×107×9.46×1012Km=D2×1.892×1020JKm
宇宙の公転軌道エネルギー=D2×1.892×1020JKm÷距離、です。
c. 半径3×107光年の軌道の秒速がDKmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=D2×3×107×9.46×1012Km=D2×2.838×1020JKm
宇宙の公転軌道エネルギー=D2×2.838×1020JKm÷距離、です。
d. 半径4×107光年の軌道の秒速がDKmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=D2×4×107×9.46×1012Km=D2×3.748×1020JKm
宇宙の公転軌道エネルギー=D2×3.748×1020JKm÷距離、です。
e. 半径5×107光年の軌道の秒速がDKmである場合。
宇宙の公転軌道エネルギー=公転速度2×中心からの距離=D2×5×107×9.46×1012Km=D2×4.73×1020JKm
宇宙の公転軌道エネルギー=D2×4.73×1020JKm÷距離、です。
・公転速度はいくらか。一般式を求める。
公転速度2=宇宙の公転軌道エネルギー
公転速度=宇宙の公転軌道エネルギー1/2
a. の場合。宇宙の公転軌道エネルギー= D2×9.46×1019JKm÷距離、です。
107光年の軌道では、速度2=D2×9.46×1019JKm
JKm÷(107×9.46×1012Km)=D2
公転速度=(D2)1/2=DKm/s、です。
2×107光年の軌道では、速度2=D2×9.46×1019JKm
÷(2×107×9.46×1012Km)=0.5D2
公転速度=(0.5D2)1/2=0.7071DKm/s、です。
3×107光年の軌道では、速度2=D2×9.46×1019JKm
÷(3×107×9.46×1012Km)=0.333D2
公転速度=(0.333D2)1/2=0.577DKm/s、です。
4×107光年の軌道では、速度2=D2×9.46×1019JKm
÷(4×107×9.46×1012Km)=0.25D2
公転速度=(0.25D2)1/2=0.5DKm/s、です。
5×107光年の軌道では、速度2=D2×9.46×1019JKm
÷(5×107×9.46×1012Km)=0.2D2
公転速度=(0.2D2)1/2=0.447DKm/s、です。
c. の場合。宇宙の公転軌道エネルギー=D2×2.838×1020JKm÷距離、です。
107光年の軌道では、速度2=D2×2.838×1020JKm÷(107×9.46×1012Km)=3D2
公転速度=(3D2)1/2=1.732DKm/s、です。
2×107光年の軌道では、速度2=D2×2.838×1020JKm÷(2×107×9.46×1012Km)=1.5D2
公転速度=(1.5D2)1/2=1.225DKm/s、です。
3×107光年の軌道では、速度2=D2×2.838×1020JKm
÷(3×107×9.46×1012Km)=D2
公転速度=(D2)1/2=DKm/s、です。
4×107光年の軌道では、速度2=D2×2.838×1020JKm
÷(4×107×9.46×1012Km)=0.75D2
公転速度=(0.75D2)1/2=0.866DKm/s、です。
5×107光年の軌道では、速度2=D2×2.838×1020JKm
÷(5×107×9.46×1012Km)=0.6D2
公転速度=(0.6D2)1/2=0.775DKm/s、です。
e. の場合。宇宙の公転軌道エネルギー=D2×4.73×1020JKm÷距離、です。
107光年の軌道では、速度2=D2×4.73×1020JKm÷(107×9.46×1012Km)=5D2
公転速度=(5D2)1/2=2.236DKm/s、です。
2×107光年の軌道では、速度2=D2×4.73×1020JKm÷(2×107×9.46×1012Km)=2.5D2
公転速度=(2.5D2)1/2=1.581DKm/s、です。
3×107光年の軌道では、速度2=D2×4.73×1020JKm
÷(3×107×9.46×1012Km)=1.666D2
公転速度=(1.666D2)1/2=1.291DKm/s、です。
4×107光年の軌道では、速度2=D2×4.73×1020JKm
÷(4×107×9.46×1012Km)=1.250D2
公転速度=(1.250D2)1/2=1.118DKm/s、です。
5×107光年の軌道では、速度2=D2×4.73×1020JKm
÷(5×107×9.46×1012Km)=D2
公転速度=(D2)1/2=DKm/s、です。
・宇宙の公転軌道は1周するのに何年かかるか。現在まで何周しているか。一般式を求める。
1周するのにかかる年数=円周÷1年間に走る距離=2×3.14×半径(光年)×9.46×1012Km÷(秒速×365×24×60×60)=1.883×半径(光年)÷秒速×106
何周しているか=137×108年÷1周するのにかかる年数=137×108年÷(1.883×半径(光年)÷秒速×106)=7.276×103×秒速÷半径(光年)
a.の場合。
107光年の軌道を公転する。公転速度=D2/2=DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×107÷D×106=1.883×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×D÷107=7.276×10−4×D
2×107光年の軌道を公転する。公転速度=0.707DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×2×107÷0.707D×106=5.327×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.707D÷(2×107)=2.572×10−4×D
3×107光年の軌道を公転する。公転速度=0.577DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×3×107÷0.577D×106=9.790×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.577D÷(3×107)=1.399×10−4×D
4×107光年の軌道を公転する。公転速度=0.5DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×4×107÷0.5D×106=1.506×1014÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.5D÷(4×107)=9.095×10−5×D
5×107光年の軌道を公転する。公転速度=0.447DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×5×107÷0.447D×106=2.106×1014÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.447D÷(5×107)=6.505×10−5×D
cの場合。
107光年の軌道を公転する。公転速度=1.732DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×107÷1.732D×106=1.087×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×1.732D÷107=1.260×10−3×D
2×107光年の軌道を公転する。公転速度=1.225DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×2×107÷1.225D×106=3.074×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×1.225D÷(2×107)=4.457×10−4×D
3×107光年の軌道を公転する。公転速度=DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×3×107÷D×106=5.649×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×D÷(3×107)=2.425×10−4×D
4×107光年の軌道を公転する。公転速度=0.866DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×4×107÷0.866D×106=8.697×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.866D÷(4×107)=1.575×10−4×D
5×107光年の軌道を公転する。公転速度=0.775DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×5×107÷0.775D×106=1.215×1014÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×0.775D÷(5×107)=1.128×10−4×D
e.の場合。
107光年の軌道を公転する。公転速度=2.236DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×107÷2.236D×106=8.421×1012÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×2.236D÷107=1.627×10−3×D
2×107光年の軌道を公転する。公転速度=1.581DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×2×107÷1.581D×106=2.382×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×1.581D÷(2×107)=5.752×10−4×D
3×107光年の軌道を公転する。公転速度=1.291DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×3×107÷1.291D×106=4.376×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×1.291D÷(3×107)=3.131×10−4×D
4×107光年の軌道を公転する。公転速度=1.118DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×4×107÷1.118D×106=6.737×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×1.118D÷(4×107)=2.034×10−4×D
5×107光年の軌道を公転する。公転速度=DKm/s、です。
1周するのにかかる年数=1.883×半径(光年)÷秒速×106=1.883×5×107÷D×106=9.415×1013÷D
何周しているか=7.276×103×秒速÷半径(光年)=7.276×103×D÷(5×107)=1.455×10−4×D
表3
|
|
a |
c |
e |
|
秒速 |
DKm |
DKm |
DKm |
|
宇宙の公転軌道エネルギー |
D2×9.46×1019JKm÷距離 |
D2×2.838×1020JKm÷距離 |
D2×4.73×1020JKm÷距離 |
|
公転速度 |
|
|
|
|
107光年の軌道 |
DKm/s |
1.732 DKm/s |
2.236 DKm/s |
|
2×107光年の軌道 |
0.707 DKm/s |
1.225 DKm/s |
1.581 DKm/s |
|
3×107光年の軌道 |
0.577 DKm/s |
DKm/s |
1.291 DKm/s |
|
4×107光年の軌道 |
0.5 DKm/s |
0.866 DKm/s |
1.118 DKm/s |
|
5×107光年の軌道 |
0.447 DKm/s |
0.775 DKm/s |
DKm/s |
|
1周するのにかかる年数 |
|
|
|
|
107光年の軌道 |
1.883×1013÷D |
1.087×1013÷D |
8.421×1012÷D |
|
2×107光年の軌道 |
5.327×1013÷D |
3.074×1013÷D |
2.382×1013÷D |
|
3×107光年の軌道 |
9.790×1013÷D |
5.649×1013÷D |
4.376×1013÷D |
|
4×107光年の軌道 |
1.506×1014÷D |
8.697×1013÷D |
6.737×1013÷D |
|
5×107光年の軌道 |
2.106×1014÷D |
1.215×1014÷D |
9.415×1013÷D |
|
何周しているか |
|
|
|
|
107光年の軌道 |
7.276×10−4×D |
1.260×10−3×D |
1.627×10−3×D |
|
2×107光年の軌道 |
2.572×10−4×D |
4.457×10−4×D |
5.752×10−4×D |
|
3×107光年の軌道 |
1.399×10−4×D |
2.425×10−4×D |
3.131×10−4×D |
|
4×107光年の軌道 |
9.095×10−5×D |
1.575×10−4×D |
2.034×10−4×D |
|
5×107光年の軌道 |
6.505×10−5×D |
1.128×10−4×D |
1.455×10−4×D |
・この事によって理解できる事。
軌道の速度を知る事によって、宇宙の公転軌道エネルギー、各々の軌道における公転速度、1周するのにかかる年数、何周しているか、を計算できる。
8. 中心のブラックホールの質量はいくらか。一般式を求め、1例を示す。
中心のブラックホールの質量が10n太陽質量であるとき、軌道エネルギーは、5.4×1018+2n/3JKm÷距離、です。この事から中心のブラックホールの質量を求める。一般式を求める。
公転速度をD(Km/s)とする。
a.銀河が半径107光年の軌道に存在し、その公転速度をD(Km/s)とする。
5.4×1018+2n/3JKm÷距離=5.4×1018+2n/3JKm÷(107×9.46×1012Km)=D2
102n/3=D2÷5.4×(107×9.46×1012Km)÷1018=1.752×10×D2=101.2435×D2
2n/3 =1.243+log D2
n=(1.243+log D2)×1.5
10n=中央のブラックホールの質量
a. 例えば、半径107光年の軌道の秒速が600Kmである場合。
n=(1.243+log D2)×1.5=(1.243+Log6002)×1.5=(1.243+ Log3.6×105)×1.5=(1.243+5.5563)×1.5=6.7993×1.5=10.19895
1010.19895=1.581×1010
中央のブラックホールの質量は、1.581×1010太陽質量です。
c. 半径3×107光年の軌道の秒速がDKmである場合。
5.4×1018+2n/3JKm÷距離=5.4×1018+2n/3JKm÷(3×107×9.46×1012Km)=D2
102n/3=D2÷5.4×(3×107×9.46×1012Km)÷1018=5.2556×10×D2=101.7207×D2
2n/3=1.7207×log D2
n=(1.7207×log D2)×1.5
10n=中央のブラックホールの質量
c. 例えば、半径3×107光年の軌道の秒速が600Kmである場合。
n=(1.7207×log D2)×1.5=(1.7207+Log6002)×1.5=(1.7207+ Log3.6×105)×1.5=(1.7207+5.5563)×1.5=7.277×1.5=10.9155
1010.9155=8.231×1010
中央のブラックホールの質量は、8.231×1010太陽質量です。
e. 半径5×107光年の軌道の秒速がDKmである場合。
5.4×1018+2n/3JKm÷距離=5.4×1018+2n/3JKm÷(5×107×9.46×1012Km)=D2
102n/3=D2÷5.4×(5×107×9.46×1012Km)÷1018=8.759×10×D2=101.9894×D2
2n/3=1.9894×log D2
n=(1.9894×log D2)×1.5
10n=中央のブラックホールの質量
e. 例えば、半径5×107光年の軌道の秒速が600Kmである場合。
n=(1.9894×log D2)×1.5=(1.9894+Log6002)×1.5=(1.9894+ Log3.6×105)×1.5=(1.9894+5.5563)×1.5=7.5457×1.5=11.31855
1011.31855=2.082×1011
中央のブラックホールの質量は、2.082×1011太陽質量です。
9. 中央のブラックホールができるために必要な質量はいくらか。
私は、2008年9月1日に提出した、特願2008−223099、において、太陽質量のB倍のブラックホールになるために必要な質量は、B×9.458×105太陽質量に成る、と示した。
それで、a,c,eの場合、ブラックホールになるために必要な質量はいくらか。
a. 例えば、半径107光年の軌道の秒速が600Kmである場合。
中央のブラックホールの質量は、1.581×1010太陽質量です。
中央のブラックホールができるために必要な質量=9.458×105×1.581×1010太陽質量=1.495×1016太陽質量
中央のブラックホールができるために必要な質量は1.495×1016太陽質量です。
c. 例えば、半径3×107光年の軌道の秒速が600Kmである場合。
中央のブラックホールの質量は、8.231×1010太陽質量です。
中央のブラックホールができるために必要な質量=9.458×105×8.231×1010太陽質量=7.785×1016太陽質量
中央のブラックホールができるために必要な質量は7.785×1016太陽質量です。
e. 例えば、半径5×107光年の軌道の秒速が600Kmである場合。
中央のブラックホールの質量は、2.082×1011太陽質量です。
中央のブラックホールができるために必要な質量=9.458×105×2.082×1011太陽質量=1.969×1017太陽質量
中央のブラックホールができるために必要な質量は1.969×1017太陽質量です。
10. 磁気の届く距離はいくらか。この距離は何光年か。
私は、2008年7月4日に提出した、特願2008−200203において、
β=軌道の全体の質量=ブラックホールになるために必要な質量とする。
磁気の届く距離=1.627×1010×β2/3Km、と示した。
a. 例えば、半径107光年の軌道の秒速が600Kmである場合。
β=軌道の全体の質量=ブラックホールになるために必要な質量=1.495×1016太陽質量
磁気の届く距離=1.627×1010×β2/3Km=1.627×1010×(1.495×1016)2/3Km=1.627×1010×14.952/3×1010Km=1.627×1010×6.069×1010Km=9.874×1020Km
磁気の届く距離は9.874×1020Kmです。
この距離は何光年か。
距離÷(9.46×1012Km)=9.874×1020Km÷(9.46×1012Km)=1.044×108(光年)
磁気の届く距離は1.044×108光年です。
c. 例えば、半径3×107光年の軌道の秒速が600Kmである場合。
β=軌道の全体の質量=ブラックホールになるために必要な質量=7.783×1016太陽質量
磁気の届く距離=1.627×1010×β2/3Km=1.627×1010×(7.783×1016)2/3Km=1.627×1010×77.832/3×1010Km=1.627×1010×18.229×1010Km=2.966×1021Km
磁気の届く距離は2.966×1021Kmです。
この距離は何光年か。
距離÷(9.46×1012Km)=2.966×1021Km÷(9.46×1012Km)=3.135×108(光年)
磁気の届く距離は3.135×108光年です。
e. 例えば、半径5×107光年の軌道の秒速が600Kmである場合。
β=軌道の全体の質量=ブラックホールになるために必要な質量=1.969×1017太陽質量
磁気の届く距離=1.627×1010×β2/3Km=1.627×1010×(1.969×1017)2/3Km=1.627×1010×196.92/3×1010Km=1.627×1010×33.845×1010Km=5.507×1021Km
磁気の届く距離は5.507×1021Kmです。
この距離は何光年か。
距離÷(9.46×1012Km)=5.507×1021Km÷(9.46×1012Km)=5.821×108(光年)
磁気の届く距離は5.821×108光年です。
表4
|
|
a |
c |
e |
|
秒速 |
DKm |
DKm |
DKm |
|
中心のブラックホールの質量はいくらか。一般式 |
n=(1.243+logD2)×1.5 |
n=(1.7207+logD2)×1.5 |
n=(1.9894+logD2)×1.5 |
|
秒速 |
600Km |
600Km |
600Km |
|
中央のブラックホールの質量 |
1.581×1010太陽質量 |
8.231×1010太陽質量 |
2.082×1011太陽質量 |
|
中央のブラックホールができるために必要な質量 |
中央のブラックホールの質量×9.458×105太陽質量 |
中央のブラックホールの質量×9.458×105太陽質量 |
中央のブラックホールの質量×9.458×105太陽質量 |
|
中央のブラックホールができるために必要な質量 |
1.495×1016太陽質量 |
7.785×1016太陽質量 |
1.969×1017太陽質量 |
|
磁気の届く距離 |
9.874×1020Km |
2.966×1021Km |
5.507×1021Km |
|
距離は何光年か |
1.044×108光年 |
3.135×108光年 |
5.821×108光年 |
・この事によって理解できる事。
現在、宇宙の軌道は約1億光年です。
この事によって、中央のブラックホールの質量を求める式も、中央のブラックホールができるために必要な質量を求める式も、磁気の届く距離を求める式も正しい事が確認できた。
中心のブラックホールの質量が10n太陽質量であるとき、軌道エネルギーは、5.4×1018+2n/3JKm÷距離、です。
軌道エネルギーは速度2です。
太陽質量のB倍のブラックホールになるために必要な質量は、B×9.458×105太陽質量です。
磁気の届く距離=1.627×1010×β2/3Km、βは全体の質量で、中央のブラックホールができるために必要な質量です。
軌道の速度を知る事によって、中央のブラックホールの質量、中央のブラックホールができるために必要な質量、磁気の届く距離を知る事ができる。
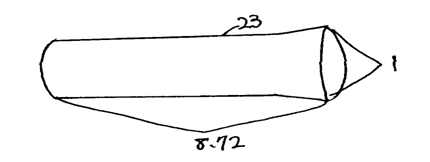
11. もし、宇宙の公転軌道が1億光年で、現在まで1公転しているとしたら、筒の長さはいくらか。
私は、2008年10月17日に提出した、特願2008−268538、「宇宙11」で、次のように記した。
螺旋回転速度2=公転速度2÷0.01254=公転速度2×79.7
このことは、螺旋回転速度=(公転速度2×79.7)1/2≒公転速度×8.927、です。
速さと距離は比例します。それで、螺旋回転で進んだ距離は公転で進む距離×8.927、です。
もし、公転で進んだ距離=軌道×3.14とすると、
筒の長さを進んだ距離は、公転で進んだ距離×8.927です。
筒の長さを進んだ距離は、公転で進んだ距離×8.927で、これは螺旋回転をしているので、筒の長さにすると、公転で進んだ距離×8.927÷3.14=公転で進んだ距離×2.843、です。
現在まで、仮に、宇宙は1公転し、公転の直径が1億光年であるとすると、宇宙の進んだ公転距離は、1億光年×3.14です。
そして、螺旋状に進んだ距離は、公転で進んだ距離×8.927=1億光年×3.14×8.927=28.03億光年です。
そして、それを筒の長さにすると、公転で進んだ距離×8.927÷3.14=公転で進んだ距離×2.843=1億光年×3.14×2.843=8.927億光年です。
即ち、筒の長さは、8.927億光年です。
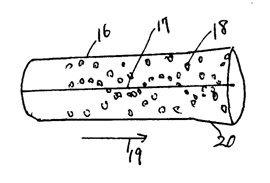
12. 宇宙の状態を筒と考えると、筒の直径は少しずつ拡大しているのはなぜか。
中央のブラックホールのエネルギーと、それを含む全体のエネルギーが引力(磁気)に成り、筒を引いている。
時間の経過とともに、そのエネルギーは弱まる。引力は弱まる。その結果筒の直径は少しずつ拡大している。
13. 中心のブラックホールはいつできたか。
中心のブラックホールはビッグバンの時にできた。
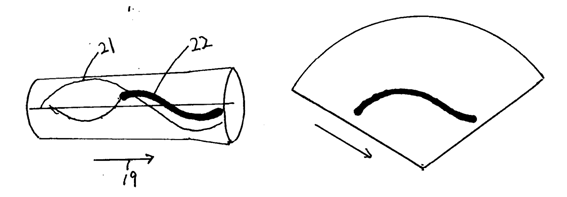
14. グレートウオールはどのようになっているのか。
遠くの銀河ほど古い時代にできた。銀河の塊がある軌道に存在します。時間と共に、軌道は進みます。軌道は螺旋状に進みます。
軌道に存在する銀河の塊も螺旋状に筒の中を進みます。それで、銀河の存在の様子は銀河が時間と共に軌道上を進んでいる事を示している。
グレートウオールはたくさんの銀河が軌道に存在し、軌道を進んでいる事を示している。
15. グレートウオールの形から、宇宙は今まで何公転したか。
グレートウオールは3億光年の距離にあり、グレートウオールは長さ5億光年以上、高さ2億光年、厚さ1500万光年程です。
グレートウオールの形から、宇宙は今まで約1公転したと推察できる。
16. 宇宙はこれからどのように進むか。
電子は陽子の周囲を螺旋回転し、地球は太陽の周囲を螺旋回転し、太陽は腕の中のブラックホールを螺旋回転し、銀河系は中心のブラックホールの周囲を螺旋回転する。
宇宙は、まるで、ホルンのように先端の公転を拡大しながら螺旋回転する。
【図面の簡単な説明】
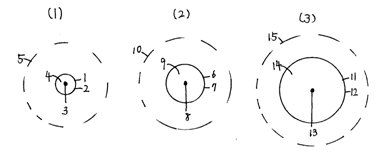
【図1】図1は其々の軌道の公転速度を600Km/sとした場合の宇宙の軌道エネルギーの説明図。
(1)図は107光年の軌道の公転速度が600Km/sであるとした場合であり、宇宙の公転軌道エネルギー=3.406×1025JKm÷距離。中心のブラックホールの質量は1.581×1010太陽質量。全体の質量は1.495×1016太陽質量。磁気の届く距離は1.044×108光年である事を示す。
(2)図は3×107光年の軌道の公転速度が600Km/sであるとした場合であり、宇宙の公転軌道エネルギー=1.022×1026JKm÷距離。中心のブラックホールの質量は8.231×1010太陽質量。全体の質量は7.785×1016太陽質量。磁気の届く距離は3.135×108光年である事を示す。
(3)図は5×107光年の軌道の公転速度が600Km/sであるとした場合であり、宇宙の公転軌道エネルギー=1.703×1026JKm÷距離。中心のブラックホールの質量は2.082×1011太陽質量。全体の質量は1.969×1017太陽質量。磁気の届く距離は5.821×108光年である事を示す。
【図2】図2は筒の中心にブラックホールがあり、全体の質量エネルギーが時間の経過とともに弱まることにより、引力が時間の経過とともに弱まり、公転軌道は拡大し、筒は少しずつ拡大する。
【図3】図3は筒の中心にブラックホールがあり、その周囲を軌道は螺旋状に回転している。螺旋状に存在する銀河団の塊も時間と共に螺旋状に進む。それで、時間と共に螺旋状に進んだ銀河団の塊は螺旋状に存在しているように観察される。これがグレートウオールです。
【図4】図4は宇宙の筒の直径を1億光年とすると、筒の長さは8.927億光年です。
【符号の説明】
1 半径107光年の軌道の公転速度は600Km/s。
2 宇宙の公転軌道エネルギー=3.406×1025Jkm÷距離。
3 中心のブラックホールの質量は1.581×1010太陽質量。
4 全体の質量は1.495×1016太陽質量。
5 磁気の届く距離は1.044×108光年。
6 3×107光年の軌道の公転速度は600Km/s。
7 宇宙の公転軌道エネルギー=1.022×1026JKm÷距離。
8 中心のブラックホールの質量は8.231×1010太陽質量。
9 全体の質量は7.785×1016太陽質量。
10 磁気の届く距離は3.135×108光年。
11 5×107光年の軌道の公転速度は600Km/s。
12 宇宙の公転軌道エネルギー=1.703×1026JKm÷距離。
13 中心のブラックホールの質量は2.082×1011太陽質量。
14 全体の質量は1.969×1017太陽質量。
15 磁気の届く距離は5.821×108光年。
16 筒
17 筒の中心のブラックホール
18 質量に成る銀河団
19 時間の経過
20 ブラックホールや全体の質量エネルギーは時間の経過とともに減少し、引力も減少し、筒は拡大する。
21 螺旋回転の軌道
22 螺旋回転する軌道の上に存在する銀河団が時間の経過とともに移動する。これがグレートウォール
23 筒の直径が1億光年とすると、筒の長さはその8.72倍の8.72億光年。
図面
【図1】
【図2】
【図3】
 【図4】
【図4】