2012�N9���̓��{�V���w��Ŕ��\�������B�u���ƃ|�X�^�[
�^�C�g���u�O���[�g�E�H�[���͂ǂ̂悤�ɂł������B�v�@
�F���̒��S��2.631�~1013���z���ʂ̃u���b�N�z�[�����ł������A�W�F�b�g���˂͂ǂ��܂œ͂������B���̋O�����a�͌��݁A�ǂꂭ�炢�̋O�����a�ɂȂ�A���ɐ����Ă��邩�B
10�|16������A�F���̒��S��2.631�~1013���z���ʂ̃u���b�N�z�[������W�F�b�g�����o���Ă����B���̃W�F�b�g�͓��������f���q�������������A�u���b�N�z�[����������B
10�|16������͓d�q�̃��u�̌��]�O����10�|16���ŁA�n�\�̓d�q�̃��u�̌��]�O����10�|6�{�ł���A���ꂪ�W�܂�ƃu���b�N�z�[�����ł��A�N�G�[�T�[�ɂȂ�B
�W�F�b�g���͂����������z�̔��a�~849�~��͂�N�G�[�T�[��A���j�Z���̏��A��6.96�~105Km�~849�~4.325�~104�~��1/3��(3.873�~103)=6.599�~109�~��1/3�B
���̓N�G�[�T�[���͂̑S�̂̎��ʂł��B
����9.458�~105�~10n�@(10n=�u���b�N�z�[���̎��ʂŁA�P�ʂ͑��z���ʁB����10n���z���ʂ̃u���b�N�z�[������邽�߂ɕK�v�ȑS�̂̎���)
����āA�W�F�b�g���͂�������6.599�~109�~��1/3��6.599�~109�~(9.458�~105�~10n)1/3Km=6.599�~109�~9.816�~10�~10n/3Km��6.478�~1011�~10n/3Km�B���̎���10�|14������̎��ł��B
�W�F�b�g�����o���������10�|16������ł���A�N�G�[�T�[���ł��鎞��ł��邩��A���̎���̃G�l���M�[�́A10�|14�������100�{�̃G�l���M�[�ł��B����ŁA�o������W�F�b�g�̃G�l���M�[��100�{�ŁA�W�F�b�g���͂�������100�{�ł��B����āA10�|16������A�W�F�b�g���͂�������6.478�~1011�~10n/3Km�~100��6.478�~1013�~(2.631�~1013)1/3Km��6.478�~1013�~26.311/3�~104Km��6.478�~1013�~2.974�~104Km��1.927�~1018Km�B
����́A1.927�~1018Km��(9.46�~1012Km)��2.037�~105�A���N�ł��B
���̋O�����a�́A10�|16�����ォ��10�|14������ɐ���A������100�{�ɖc�������̂ŁA2.036�~107���N�ɐ���܂����B���ꂪ�O���[�g�E�H�[���ł��B
����
�y�}�ʂ̐����z�@
�@10�|16m����A�F���̒�����2.631�~1013���z���ʂ̃u���b�N�z�[������W�F�b�g�����o�����B���̏�̃G�l���M�[�́A����̉F����102�{�̃G�l���M�[�̏�ł���B
����ŁA�W�F�b�g���͂�������6.599�~109�~��1/3Km�~102��6.599�~109�~(9.458�~105�~10n)1/3Km�~102��6.478�~1011�~10n/3Km�~102��6.478�~1011�~(2.631�~1013)1/3Km�~102��6.478�~1011�~26.311/3�~104 Km�~102��6.478�~1011�~2.974�~104 Km�~102��1.927�~1018Km�B���̋O�����a�́A1.927�~1018Km��(9.46�~1012Km)��2.037�~105�@���N�ł��B
10�|16m����W�F�b�g�͋O�����a2.037�~105�@���N�܂œ͂��A���̋O�����a�ɂ�������̃N�G�[�T�[��������B
���̋O�����a��10�|16m���ォ��A10�|14m����ɐ���A100�{�Ɋg�債���̂ŁA���̋O�����a�͌���2.037�~105�@���N�~100��2.037�~107�@���N�A�ł��B
����ŁA���݁A�O�����a2.037�~107�@���N�̋O���ɂ�������̋�͂����݂���B
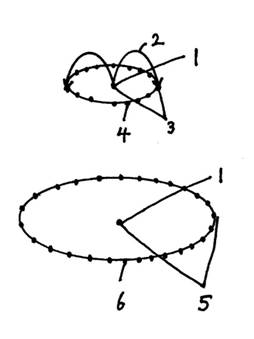
�y�����̐����z
�@�P�@�@�F���̒��S�̃u���b�N�z�[��
�@�Q�@�@�W�F�b�g
�@�R�@�@10�|16m����A�W�F�b�g���͂����O�����a��2.037�~105���N
�@�S�@�@�N�G�[�T�[
�@�T�@�@10�|14m����A�W�F�b�g���͂����O�����a��2.037�~107���N
�@�U�@�@���
�y�}�z
�Q��
���W�F�b�g���͂����������z�̔��a�~849�~(��͂�N�G�[�T�[��)A���j�Z���̏��A�A�̎����ł��闝�R�B
�@����f���̐��f�͂ǂ̂悤�ɂł������B
���̎��ʂƐ��̒��S��A�͐���Ⴕ�܂��B
���̎��ʁ����̒��S��A�����z�̎��ʁ����z�̒��S��A�@�ł��B
�W�F�b�g�����łł������̎��ʂ́A�W�F�b�g������ɂł����f���̎��ʂ̂��{�ł���Ƃ��܂��B
�n���̎��ʁ��n���̒��S��A�����z�̎��ʁ����z�̒��S��A�~��
���z�̎��ʂ�1�Ƃ���ƁA�n���̎��ʂ�3.0404�~10�|6�ł��B
�n���̒��S�̉��x�́A7600K=7327 ���ł�����A�n���̒��S��A=(7327)1/2=85.6�B
���z�̒��S�̉��x�́A1.5�~107���ł��邩��A���z�̒��S��A=(1.5�~107)1/2=3.873�~103�B
�n���̎��ʁ��n���̒��S��A�����z�̎��ʁ����z�̒��S��A�~��
�����n���̎��ʁ��n���̒��S��A �����z�̎��ʁ~���z�̒��S��A
��3.0404�~10�|6��85.6��1�~3.873�~103��1.376�~10�|4
�����A
�n���̎��ʁ��n���̒��S��A�����z�̎��ʁ����z�̒��S��A�~1.376�~10�|4
�n���̎��ʁ��n���̒��S��A�����̎��ʁ����̒��S��A�~1.376�~10�|4
���̎��ʁ��n���̎��ʁ��n���̒��S��A�~���̒��S��A��(1.376�~10�|4)���n���̎��ʁ�85.6�~���̒��S��A��(1.376�~10�|4)���n���̎��ʁ~���̒��S��A�~84.9
���̎��ʁ��n���̎��ʁ~���̒��S��A�~84.9
���̏ꍇ�B
���̎��ɂ���ė����ł��鎖�́A���z��̂悤�ɁA���n���̂Ƃ��A�W�F�b�g���˂��Ăł������̎��ʂ́A�n���̂悤�ɃW�F�b�g���˂��Ȃ������f���̎��ʂ�84.9�~���̒��S��A�{�̎��ʂɐ���B�Ƃ������Ƃł��B
���̓W�F�b�g���˂��鎖�ɂ���āA�f���̎��ʁ~84.9�~���̒��S��A�{�̐��f���l���ł����B
�W�F�b�g���˂��鎖�ɂ���āA84.9�~���̒��S��A�{�̃_�[�N�}�^�[���l���ł����B
�f���̏ꍇ�B
�n���C�͒n���̔��a��10�{�����܂ŋy�т܂��B����ŁA�n���C�ɂ���Ĕ��ꂽ��Ԃ̃_�[�N�}�^�[�����]�����f�ɐ���n���ɏW�܂����B
�n���̒n���C�͒n���̔��a��10�{�����܂œ͂��܂��B
����ŁA���z�̌��n�����o���W�F�b�g���˂́A���z�̔��a��10�~84.9��849�{�܂œ͂����B
�Q��
���ΐ��Ɩؐ��̊Ԃ̏��f���̋N��
���z�̌��n���̊j�Z���łł����W�F�b�g���˂��͂����������z�̔��a��10�~84.9�~�j�Z��
�̏��A�����z�̒��S��A�����z�̔��a�~849�~(3.873�~103)��(3.873�~103)��6.96�~105Km�~849��5.909�~108Km
���̋����́A�ؐ��Ɖΐ��̊Ԃł��B
���G�b�W���[�X�E�J�C�p�[�x���g�̏��f���̋N��
���z�̒��S�̒����q���o���W�F�b�g���˂��͂����������z�̔��a�~849�~�����q����A�����z�̒��S��A=6.96�~105Km�~849�~1.968�~105��(3.873�~103)��3.002�~1010Km
���̋����ɂ́A�G�b�W���[�X�E�J�C�p�[�x���g�̏��f�������݂��܂��B
���I���g�[�̉_�̋N��
���z�̐e�ł����1����̐��̒��S�̃u���b�N�z�[�����o���W�F�b�g���˂��͂����������z�̔��a�~849�~�u���b�N�z�[����A�����z�̒��S��A=6.96�~105Km�~849�~7.375�~105��(3.873�~103)��1.125�~1011Km
�I���g�[�̉_�̓u���b�N�z�[������1.125�~1011Km�̋O���ɂł������A���ꂩ���100���N��̌��݁A������100�{�ɐ���A1013Km�̋O���ɑ��݂���B
����́A2010�N�R���̓��{�V���w��̃|�X�^�[�B�^�C�g���u���f���ƃG�b�W���[�X�E�J�C�p�[�x���g�̏��f�����I�[���g�̉_�̐����v�Ƃ͎�Ⴂ�܂��B2010�N�R���̓��{�V���w��̃|�X�^�[�́A�u���b�N�z�[���ƒ����q���̎��ʂz���ʂ�5/1�Ƃ��Ă��܂��B���̕K�v�͂���܂���B
���W�F�b�g���˂����f������錴��
�W�F�b�g�͓d�q�̃��u�Ɨz�q�̃��u����鎥�C�̌��q�Ɠd�C�̌��q�Ȃ̂ŁA�����������]���Ă���d�q�̃��u��z�q�̃��u(�_�[�N�}�^�[)�������������A���]������B�����āA���f�ɂ�����B���̐��f���������A���f�������B
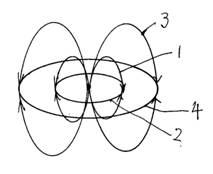
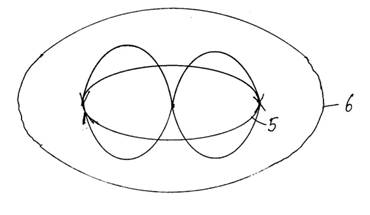
�y�����̐����z
�P�@���z�̌��n���̊j�Z���łł����W�F�b�g���˂��͂�������5.909�~108Km
�Q�@�ΐ��Ɩؐ��̊Ԃ̏��f���̋O��
�R�@���z�̒��S�̒����q���o���W�F�b�g���˂��͂�������3.002�~1010Km
�S�@�G�b�W���[�X�E�J�C�p�[�x���g�̏��f���̋O��
�T�@���z�̐e�ł����1����̐��̒��S�̃u���b�N�z�[�����o���W�F�b�g���˂��͂�������1.125�~1011Km
�U�@�I���g�[�̉_�̋O����100�{�ɐ���A1013Km�ɂȂ����B
�y�}�z
�W�F�b�g������������ɂł��镨
|
10�|16�����ȑO |
�N�G�[�T�[�����u���b�N�z�[���B |
|
10�|16�� |
�N�G�[�T�[�B |
|
10�|15�� |
�N�G�[�T�[�͋�͂ɐ���B���B��G�l���M�[�̏�ł͏��f�� |
|
10�|14�� |
���G�l���M�[�̏�ł͐��B���f���B |
�Q��
����͂�N�G�[�T�[��A=4.325�~104�~��1/3�ł��闝�R�B
�@���z�̃��{�̃N�G�[�T�[���ł��邽�߂ɂ́A�ǂ�ʂ̑̐ς̌��q���W�߂Ăł������B����͔��a��Km���B(2007�N8��25���ɒ�o�����A����2007�|246139�ɋL����)
10�|16m�̎���A�F���͂ǂ̏�ł��A�Tm3��1018�̌��q�����݂��Ă����Ƃ��܂��B
�N�G�[�T�[�̌��q�������z�̌��q���~����1.2�~1057�~��
�̐ς���m3�Ƃ��܂��B
1018�~��m3��1.2�~1057�~��
��m3��1.2�~1057�~����1018��1.2�~1039�~��
�̐ς́A1.2�~1039�~��m3�ł��B
4��3�~��3��1.2�~1039�~��m3
��3��1.2�~1039�~��m3��4�~3��2.866�~1038�~��m3
r��(2.866�~1038�~��m3)1/3=6.6�~1012�~��1/3m=6.6�~109�~��1/3Km
���a��6.6�~109�~��1/3Km�ł��B
���̔��a�ɃW�F�b�g�͓͂����B
�W�F�b�g���͂����������z�̔��a�~849�~��͂�N�G�[�T�[��A���j�Z���̏��A��6.96�~105Km�~849�~��͂�N�G�[�T�[��A��(3.873�~103)= 6.6�~109�~��1/3Km
��͂�N�G�[�T�[��A��6.6�~109�~��1/3Km��(6.96�~105Km�~849)�~3.873�~103��4.326�~104�~��1/3
����āA��͂�N�G�[�T�[��A��4.326�~104�~��1/3�A�ł��B
2011�N3���̓��{�V���w��@�Ŕ��\�������B�|�X�^�[�u��
�^�C�g���u�V�����̎��]�������]�ʂɑ���98�x�X���Ă���̂͂Ȃ����B�v
�@��͌n�̘r�́A��͌n�̒��S�̃u���b�N�z�[���̉e�����A�����Ƌ߂��r�̒��S�̃u���b�N�z�[���̉e�����邽�߁A�r�̒��S�̃u���b�N�z�[���𒆐S�ɗ�����]���Ă���B����Ɠ����悤�ɁA�V�����́A���z�̉e�����A�����̒��S�̉e�����Ă���B���̂��߁A�V�����͗�����]�����Ă���B�V�����̌��]�̋O���G�l���M�[�����]���x2��6.812�i��46.376�i�B�V�����̗�����]���x2�����]���x2�~79.7��46.376Km�~79.7��3696.175Km�B�V�����̗�����]���x��(3696.175)1/2Km/s=60.796Km/s�B�V�����͕b��60.796Km�ŗ�����]���Ȃ���A���z�̎�����A�b��6.81Km�Ō��]���Ă���B������]�̋O���G�l���M�[��������]���镨�̂̕\�ʂ̌��q���~1�̌��q�����d�C�̌��q1�̃G�l���M�[�ł��B�V�����̕\�ʂ̌��q����6.909�~1035�ł��B�V�����̗�����]�̋O���G�l���M�[��������]���x2��60.7962�i��3696.175J���V�����̕\�ʂ̌��q���~1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�B1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[��3.691�~103�i��(6.909�~1035��)��5.35�~10�|33�i�B1�̌��q�ŁA5.35�~10�|33�i�̓d�C�̌��q���ł���B�d�C�̌��q�̋O����1.233�~10�|41�i�����d�C�̌��q�P�̃G�l���M�[��1.233�~10�|41�i����(5.35�~10�|33�i)��2.3�~10�|9���B�d�q�̃��u�̌��]�O���́A�d�C�̌��q�̋O���ɓ���������A���̓d�q�̃��u�̌��]�O���́A2.3�~10�|9���ł��B�E���̏�̂`�͂����炩�BA�͒n�\�̉��{�̃G�l���M�[���������B�n�\�̓d�q�̃��u�̌��]�O����A��1.058�~10�|10�����`��2.3�~10�|9���B�`��1.058�~10�|10����(2.3�~10�|9��)��4.6�~10�|2�B�E���̏�̉��x�͂����炩�B���x���`2��(4.6�~10�|2)2��2.116�~10�|3��0.002116(��)�B���̏�̉��x�́A0.002116���ł��B���̉��x�̒l�́A�V���������z����镟�˗ʂ́A�n����1�Ƃ���ƁA0.0027�Ƃقړ������B
����
�P�D�@�V�����̎��]�������]�ʂɐ����Ȑ��ɑ���98�x�X���Ă���̂͂Ȃ����B
�Q�D�@�C�����̎��]�������]�ʂɐ����Ȑ��ɑ���28.8�x�X���Ă���̂͂Ȃ����B
�@��͌n�̘r�́A��͌n�̒��S�̃u���b�N�z�[���̉e���ɂ��A�����Ƌ߂��r�̒��S�̃u���b�N�z�[���̉e�����邽�߁A�r�̒��S�̃u���b�N�z�[���𒆐S�ɗ�����]���Ă���B����Ɠ����悤�ɁA�V������C�����́A���z���牓������Ă��邽�߁A���z�̉e�����A�����̒��S�̋������f�̉e�����Ă���B���̂��߁A�V�����ƊC�����͗�����]�����Ă���B
�}
���́A�|�X�^�[�u���ŁA��1����̐����u���b�N�z�[���ł��������A�g��1����̖ؐ��h�g��1����̓y���h�g��1����̓V�����h�g��1����̊C�����h���ł��������L�����B
���̎���\�ɂ��߂��B
|
|
�g��1����̖ؐ��h |
�g��1����̓y���h |
�g��1����̓V�����h |
�g��1����̊C�����h |
|
�O�����͂łł�����1����̘f���̎��� |
�n����136�{ |
�n����40�{ |
�n����9.77�{ |
�n����4.31�{ |
|
��1����̘f���̏�� |
�������f |
�������f |
�������f |
�������f |
|
��1����̘f���̎��ʂ́A���݂̘f���̎��ʂ̉��p�[�Z���g���B |
�n����136�{���n����317.83�{�~100��42.79�� |
�n����40�{���n����95.16�{�~100��42.03�� |
�n����9.77�{���n����14.54�{�~100��67.19�� |
�n����4.31�{���n����17.15�{�~100��25.13�� |
�V�����ƊC�����͗�����]���Ă��܂��B
�V�����ƊC�����́A���z��艓������Ă���̂ŁA�����̒����ɑ��݂���������f�̎��ʂ̉e���������Ă��܂��B�����āA���z����̉e�����Ă��܂��B
���ꂪ���]���̌X���Ɍ���Ă��܂��B
���]���̌X���́A�������̋������f�̎��ʁ����z����̋����A�ɔ�Ⴗ��B
���]���̌X�����萔�~�������f�̎��ʂ��n�����ʂ̉��{�ł��邩���f���Ƒ��z�̊Ԃ̋����A
���̎��ŕ\���B
�V�����̏ꍇ�B
�V�����̎��]���͌��]�O���ʂɐ����Ȓ����ɑ���98�x�X���Ă���B
�V�����̒����̋������f�̎��ʂ͒n���̎��ʂ�9.77�{�ł��B�����āA���z����̋����́A28.750�~108Km�ł��B
98�x��K�~9.77��(28.750�~108Km)
K=98�x�~28.750�~108Km��9.77��288.383�~108Km�x
K�̒l��288.383�~108Km�x�ł��B
�C�����̏ꍇ�B
�C�����̎��]���͌��]�O���ʂɐ����Ȓ����ɑ���28.8�x�X���Ă���B
�C�����̒����̋������f�̎��ʂ͒n���̎��ʂ�4.31�{�ł��B�����āA���z����̋����́A45.044�~108Km�ł��B
K�̒l��288.383�~108Km�x�Ƃ���ƁA�C�����̎��]���͌��]�O���ʂɐ����Ȓ����ɑ��ĉ��x�X���Ă��邩�B
K=288.383�~108Km�x��X�~45.044�~108Km��4.31
X=288.383�~108Km�x�~4.31��(45.044�~108Km)��27.59�x
27.59�x�X������B
����āA������]���Ă���f���̎��]���̌��]�O���ʂɐ����Ȓ����ɑ���X���́A
���]���̌X�����萔�~�������f�̎��ʂ��n�����ʂ̉��{�ł��邩���f���Ƒ��z�̊Ԃ̋�����288.383�~108Km�x�~�������f�̎��ʂ��n�����ʂ̉��{�ł��邩���f���Ƒ��z�̊Ԃ̋����A�̎��ŕ\�����B
�C�����̌X���𒆐S�ɍl����ƒ萔�́A300.99�~108K���x�ł���A�V�����̌X����102�x�ł��B
|
�萔 |
�X�� |
|
288.383�~108K���x |
�V������98�x |
|
300.99�~108K���x |
�V������102.28�x |
�R�D�@�V�����͂ǂ̂悤�ɗ�����]���Ă��邩�B
�E�f���̌��]�O���G�l���M�[�͌��]���x2�ł���B���̎��Ɋւ��Ă͎����������B
����ŁA
�V�����̌��]�̋O���G�l���M�[�����]���x2��6.812�i��46.376�i�B
�E������]���x2�����]���x2�~79.7�ł���B
������]�̑��x2�͌��]���x2�̉��{���B
�������r�́A�i1569Km/s�j2���i175.8Km/s�j2=2.462�~106���i3.091�~104�j��79.65�{�B
���ʂ̘r�́A�i2354Km/s�j2���i263.7Km/s�j2=5.541�~106���i6.954�~104�j��79.68�{�B
�傫���r�́A�i3138.7Km/s�j2���i351.6Km/s�j2=9.851�~106���i1.236�~105�j��79.70�{�B
������]�̑��x2�́A���]�̑��x2��79.68�{�ł��B
����ŁA
�V�����̗�����]���x2�����]���x2�~79.7��46.376Km�~79.7��3696.175Km�B
�V�����̗�����]���x��(3696.175)1/2Km/s=60.796Km/s�B
����āA
�V�����͕b��60.796Km�ŗ�����]���Ȃ���A���z�̎�����A�b��6.81Km�Ō��]���Ă���B
�S�D�@�V�����̕\�ʂ�1�̌��q�͂ǂ̂悤�ɂȂ��Ă��邩�B
������]�̋O���G�l���M�[��������]���镨�̂̕\�ʂ̌��q���~1�̌��q�����d�C�̌��q1�̃G�l���M�[�ł��B
�V�����̕\�ʂ̌��q����6.909�~1035�ł��B
�V�����̗�����]�̋O���G�l���M�[��������]���x2��60.7962�i��3696.175J���V�����̕\�ʂ̌��q���~1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�B
1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[��3.691�~103�i��(6.909�~1035��)��5.35�~10�|33�i�B
1�̌��q�ŁA5.35�~10�|33�i�̓d�C�̌��q���ł���B
�d�C�̌��q�̋O����1.233�~10�|41�i�����d�C�̌��q�P�̃G�l���M�[��1.233�~10�|41�i����(5.35�~10�|33�i)��2.3�~10�|9���B
�d�q�̃��u�̌��]�O���́A�d�C�̌��q�̋O���ɓ���������A���̓d�q�̃��u�̌��]�O���́A2.3�~10�|9���ł��B
�T�D�@�V�����̉��x�͂����炩�B
�E���̏�̂`�͂����炩�BA�͒n�\�̉��{�̃G�l���M�[���������B
�n�\�̓d�q�̃��u�̌��]�O����A��1.058�~10�|10�����`��2.3�~10�|9���B
�`��1.058�~10�|10����(2.3�~10�|9��)��4.6�~10�|2�B
�E���̏�̉��x�͂����炩�B���x���`2��(4.6�~10�|2)2��2.116�~10�|3��0.002116(��)�B
���̏�̉��x�́A0.002116���ł��B
���̉��x�̒l�́A�V���������z����镟�˗ʂ́A�n����1�Ƃ���ƁA0.0027�Ƃقړ������B
�U�D�@�C�����͂ǂ̂悤�ɗ�����]���Ă��邩�B
�C�����̌��]�̋O���G�l���M�[�����]���x2��5.442�i��29.594�i
�C�����̗�����]�̋O���G�l���M�[��������]���x2�����]���x2�~79.7��29.5936�i�~79.7��2358.6�i
������]���x��(2358.6)1/2=48.566Km
�C�����̗�����]�̋O���G�l���M�[��������]���x2��48.5662�i��2358.6J
�C�����͕b��48.566Km�ŗ�����](���])���Ȃ���A���z�̎�����A�b��5.44Km�Ō��]���Ă���B
�V�D�@�C�����͎��]���Ă���̂�������]���Ă���̂��B
���]�̏ꍇ�A1���]�Ői�ދ����͂����炩�B
1�����鋗���́A2����2�~�~�C�����̔��a��2�~3.14�~2.4764�~104Km��1.555�~105Km�ł��B
�C������1���]��������́A0.671���ł��B
�b��48.566Km��0.671�����鋗���́A
48.566Km�~0.671�~24�~60�~60��2.816�~106Km�ł��B
����́A1���]�̉��{�̋������B
2.816�~106Km��(1.555�~105Km)��1.811�~10
1���]��18.11�{�̋����ł��B
����āA�C�����͗�����]���Ȃ��玩�]���Ă���B�@
�W�D�@�C�����̕\�ʂ�1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�͂����炩�B
�C�����̕\�ʂ̌��q����6.101�~1035�ł��B
2.359�~103�i��(6.101�~1035��)��3.867�~10�|33�i
1�̌��q��1���]�ō��d�C�̌��q1�̃G�l���M�[��3.867�~10�|33�i�ł��B
�E���̓d�q�̃��u�̌��]�O���͂����炩�B
1.233�~10�|41�i����(3.867�~10�|33�i)��3.189�~10�|9��
���̓d�q�̃��u�̌��]�O���́A3.189�~10�|9���ł��B
�E���̏�̂`�͂����炩�B
�`��1.058�~10�|10����(3.189�~10�|9��)��3.318�~10�|2
���̏�̂`�́A3.318�~10�|2�ł��B
�X�D�@�C�����̉��x�͂����炩�B
���x���`2��(3.318�~10�|2)2��1.1�~10�|3��0.0011(��)
���̏�̉��x�́A0.0011���ł��B
�C�����̕\�ʂ̂P���q�����1�̓d�C�̌��q�̃G�l���M�[�́A3.867�~10�|33�i�ł��B
�C�����̕\�ʂ̓d�q�̃��u�̌��]�O���́A3.189�~10�|9���ŁA���̏�̂`��3.318�~10�|2�ŁA���̏�̉��x�́A0.0011���ł��B
���̒l�́A�C���������z������t�˗ʂ͒n����1�Ƃ���ƁA0.0011�Ɠ������B
�n�����P���Ƃ���ƁA0.0011���ł��B
������܂Ƃ߂ĕ\�Ɏ����B
|
|
���]���x |
���]�O���̃G�l���M�[ |
�����O���̃G�l���M�[ |
������]���x |
�\�ʂ̌��q�� |
1���q��1���]�ō��d�C�̌��q�P�̃G�l���M�[ |
�d�q�̃��u�̌��]�O�� |
���̏�̂` |
���̏�̉��x |
���z�����t�˗� |
|
�V���� |
6.81 |
46.376�i |
3696.175�i |
60.796Km
|
6.909�~1035�� |
5.35�~10�|33�i |
2.3�~10�|9�� |
4.6�~10�|2 |
0.002116�� |
0.0021 |
|
�C���� |
5.44 |
29.594�i |
2358.6�i |
48.566Km |
6.101�~1035�� |
3.867�~10�|33�i |
3.189�~10�|9�� |
3.318�~10�|2 |
0.0011�� |
0.0011 |
���̎��ɂ���ė����ł��邱�ƁB
1�D���z������t�˗ʂƓ����G�l���M�[��f���̕\�ʂ̌��q�͍���Ă���B
2�D������]���x2��������]�̋O���G�l���M�[�̍l���͐������B
3�D������]�̋O���G�l���M�[���\�ʂ̌��q���~1���q��1���]�ō��d�C�̌��q�⎥�C�̌��q�̃G�l���M�[
2009�N3���̓��{�V���w��Ŕ��\���鎖�B�u��
�^�C�g���u��͌n�̘r�͂ǂ����Č`��ς����ɐi��ł���̂��B�v�^�C�g�����Ԉ���ĕ\������Ă����B�u��͌n�̘r��3��ނɕ��ނ���B�r�̗�����]���x�͂����炩�B�v�͊Ԉ���ċL�ڂ��ꂽ���̂ł��B
����
�u��̘͂r���`��ς����ɉ�]���闝�R�v�����̏ڍׂ��L���B
��������]�Ɨ�����]�ɂ���Đi�ދ����ɂ��āB
�P�D�@���]�͘r�̗�����]�ɂ���Ăł���B
�E���z�n�̋O����2.8�����N�ŁA�Q���N�łP���]���܂��B���̕b���͂����炩�B
�b�����P���͂����������P�T�ɗv�����b����2�~2.8�~104�~9.46�~1012�j�����i2�~108�~365�~24�~60�~60�b�j��2.637�~102�j��
1�b�Ԃ�2.637�~102�j���i�ށB���̑��x�͈��ł��B
�E���z�n��200���N�ŁA�r��1�T����B���̗��R�́A�n���C��100���N�Ŗk�ɂƓ�ɂ�����ւ�邩��ł��B
�E���z�n��200���N�ŁA���j���i�ނ��B
200���N�̕b���~�b����2�~106�~365�~24�~60�~60�b�~2.637�~102�j����1.663�~108�j���i�ށB
�E���z�n��������r�̔��a�́A2500���N�ł��B200���N��1��]���܂��B
���a��2500�~9.46�~1012�j����2.365�~1016�j��
�E���z�n��������]����b���͂����炩�B
�b�����r�̉~����200���N�i�b�j��2�~3.14�~2.365�~1016�j�����i2�~106�~365�~24�~60�~60�b�j��2.354�~103�j��
���z�n�́A�r���S�̂̃u���b�N�z�[�������S�ɕb��2.354�~103�j���ŗ�����]���A��͌n�̒��S�̃u���b�N�z�[���𒆐S�ɕb��263.8�j���Ō��]����B
�Q�D�@��͌n�̘r���R��ނɕ��ނ���B
�����Șr�ƁA���ʂ̘r�ƁA�傫�Șr�ɕ��ނ���B
�����Șr�̔��a���Q�����N�A�����炢�̘r�̔��a���R�����N�A�傫�Șr�̔��a���S�����N�Ƃ���B
�r�̌`��ς����ɉ�]���邽�߂ɂ́A�r�̑��x�́A���a�ɔ�Ⴕ�Ȃ���Ȃ�Ȃ��B
�������r�̑��x�F���ʂ̘r�̑��x�F�傫�Șr�̑��x���Q�F�R�F�S
�r�̋O���G�l���M�[�́A�O���G�l���M�[�����x2�~���a�@�ł�����A
�r�̋O���G�l���M�[�̔�́A
�����Șr�̋O���G�l���M�[�F���ʂ̘r�̋O���G�l���M�[�F�傫�Șr�̋O���G�l���M�[��22�~2�F32�~3�F42�~4��8�F27�F64�@�ł��B
���ʂ̘r�̐i�ޑ��x�́A263.7�j���ł��B���̗��R�́A���z�n�͒��ʂ̘r��1�̐��ŁA���x��263.7�j���ł��邩��ł��B
�������r�̑��x�́A263.7�j���~2/3=175.8Km�ł��B
�傫�Șr�̑��x�́A263.7Km�~4/3=351.6Km�ł��B
�r�̃G�l���M�[�́A���x2�ł�����A
�����Șr�̃G�l���M�[���i175.8�j���j2��3.091�~104�i
���ʂ̘r�̃G�l���M�[���i263.7�j���j2��6.954�~104�i
�傫�Șr�̃G�l���M�[���i351.6�j���j2��1.236�~105�i�ł��B
���̃G�l���M�[����邽�߂ɂ́A�r�̒��S�̃u���b�N�z�[���̋O���G�l���M�[�͂�����łȂ���Ȃ�Ȃ����B
�r�̔��a��2500���N��2.365�~1016�j��
���]�̋O���G�l���M�[���G�l���M�[�~���a�����]���x2�~�r�̔��a
�������r�̋O���G�l���M�[��3.091�~104�i�~2.365�~1016�j����7.310�~1020�i�E�j��
���ʂ̘r�̋O���G�l���M�[��6.954�~104�i�~2.365�~1016�j����1.645�~1021�i�E�j��
�傫�Șr�̋O���G�l���M�[��1.236�~105�i�~2.365�~1016�j����2.923�~1021�i�E�j���ł��B
���ʂ̘r�́A200���N�ŗ�����ɂP��]���A1.66�~108�j���i�݂܂��B
������]���鑬�x�́A
1��]�̋�����200���N�i�b�j���r�̉~����200���N�i�b�j��2�~3.14�~2.365�~1016�j�����i2�~106�~365�~24�~60�~60�b�j��2354�j���ł��B
���ʂ̘r�́A1�b�Ԃ�2354�j��������]���A263.7�j���i�ށB
�i�ޕ�����263.7�j����2354�j����0.112
������ɑ���A��1/10���]��������ɐi�ށB
���ʂ̘r�́A1�b�Ԃ�2354�j��������]���A263.7�j���i�ނ̂ŁA
�������r�́A1�b�Ԃ�175.8�j���i�ނ��߂ɂ́A2354�j���~175.8��263.7��1569.3�j��������]����Ƃ悢�B
�������r��������]���鑬�x�́A1569.3�j���ł��B
�傫���r�́A1�b�Ԃ�351.6�j���i�ނ��߂ɂ́A2354�j���~351.6��263.7��3138.7�j��������]����Ƃ悢�B
�傫���r��������]���鑬�x�́A3138.7�j���ł��B
�������r��������]���A�i�ދ����̊����́A
175.8��1569.3��0.112�ł��B
�傫���r��������]���A�i�ދ����̊����́A
351.6��3138.7��0.112�ł��B
������]��0.112�͐i�s�����Ɍ������Đi�ށB
������܂Ƃߕ\�Ɏ����B
|
�r�̎�� |
���a |
���x�� |
�O���G�l���M�[ |
���x |
�G�l���M�[ |
���]�O���G�l���M�[ |
|
�������r |
2�����N |
2 |
8 |
175.8Km |
3.091�~104�i |
7.310�~1020�i�EKm |
|
���ʂ̘r |
3�����N |
3 |
27 |
263.7Km |
6.954�~104�i |
1.645�~1021�i�EKm |
|
�傫���r |
4�����N |
4 |
64 |
351.6Km |
1.236�~105�i |
2.923�~1021�i�EKm |
|
�r�̎�� |
������]�̑��x |
������]���i��(���]����)�����̊��� |
|
�������r |
1569.3Km |
0.112 |
|
���ʂ̘r |
2354Km |
0.112 |
|
�傫���r |
3138.7Km |
0.112 |
�R�D�@���]�̕b��2�ƋO���̃G�l���M�[�̊W�͂ǂ̂悤�ɐ����Ă���̂��B������]�̕b��2�ƋO���G�l���M�[�̊W�͂ǂ̂悤�ɂȂ��Ă��邩�B�ǂ����Ă��̂悤�ɐ����Ă���̂����̗��R�͉����B
�A���A���z�n����r�̒��S�̃u���b�N�z�[���𒆐S�ɉ�]���邱�Ƃ𗆐���]�A���z�n���������]���Ȃ���A��͂̒��S�̃u���b�N�z�[���𒆐S�ɉ�]���邱�Ƃ����]�Ƃ���B
�b���ƋO���G�l���M�[�̊W�́A�{���A�O���G�l���M�[���O���̃G�l���M�[�~���a�����x2�~���a�ł��B
������]�̋O���G�l���M�[���������x2�~�r�̔��a
�������r�̗�����]�̋O���G�l���M�[���i1569�j���j2�~2.365�~1016�j����5.822�~1022�i�E�j��
���ʂ̘r�̗�����]�̋O���G�l���M�[���i2354�j���j2�~2.365�~1016�j����1.311�~1023�i�E�j��
�傫���r�̗�����]�̋O���G�l���M�[���i3138.7�j���j2�~2.365�~1016�j����2.330�~1023�i�E�j���ł��B
��ɋ��߂��A�r�̌��]�̋O���G�l���M�[�͂��̒l�̉��{���B
���]�̋O���G�l���M�[��������]�̋O���G�l���M�[��
�������r�A7.310�~1020�i�EKm���i5.822�~1022�i�E�j���j��1.256�~10�|2�{�ɂȂ��Ă���B
���ʂ̘r�A1.645�~1021�i�EKm���i1.311�~1023�i�E�j���j��1.255�~10�|2�{�ɂȂ��Ă���B
�傫���r�A2.923�~1021�i�EKm���i2.330�~1023�i�E�j���j��1.255�~10�|2�{�ɂȂ��Ă���B
���̎��́A�r�̗�����]�́A1.255�~10�|2�{�̃G�l���M�[�ʼn�]�ł��鎖�������B
���̗��R�́A���x2���傫������ł��B
���x2�̔�r�B
������]�̑��x2�͌��]���x2�̉��{���B
�������r�́A�i1569Km/s�j2���i175.8Km/s�j2=2.462�~106���i3.091�~104�j��79.65�{�B
���ʂ̘r�́A�i2354Km/s�j2���i263.7Km/s�j2=5.541�~106���i6.954�~104�j��79.68�{�B
�傫���r�́A�i3138.7Km/s�j2���i351.6Km/s�j2=9.851�~106���i1.236�~105�j��79.70�{�B
������]�̑��x2�́A���]�̑��x2��79.68�{�ł��B
�����]���x2���傫���̂ŃG�l���M�[��1.255�~10�|2�{�ł悢�B
�r�̋O���G�l���M�[���]���̑��x2�~���a��1.256�~10�|2�{�ł悢���R�́A���x2��79.68�{�ł��邩��ł��B
���̎��ɂ���ė����ł������ƁB
�O���̃G�l���M�[�����x2�A�ł���̂́A���]�O���̏ꍇ�ł���A�����O���̏ꍇ�͋O���̃G�l���M�[�~79.68�����x2�ł���B
�S�D�@���]���鑬�x2���O���̃G�l���M�[�A�̒l�͂ǂ̂悤�ł��邩�B������]���鑬�x2���O���̃G�l���M�[�A�̒l�͂ǂ��ł��邩�B
�E���]���鑬�x2���O���̃G�l���M�[�̒l�͂ǂ̂悤�ł��邩�B
�������r�A175.82Km��(3.091�~104J)��1
���ʂ̘r�A263.72Km��(6.954�~104J)���P
�傫���r�A351.62Km��(1.236�~105J)���P
�E������]���鑬�x2���O���̃G�l���M�[�̒l�͂ǂ��ł��邩�B
�������r�A1569.32Km��(3.091�~104J)��79.65
���ʂ̘r�A23542Km��(6.954�~104J)��79.68
�傫���r�A3138.72Km��(1.236�~105J)��79.7
���̎����痝���ł��邱�ƁB
1�D���]�̏ꍇ�A�O���̃G�l���M�[�͑��x2�ɕϊ������B
2�D������]�̏ꍇ�A�O���G�l���M�[��79.7�{�����x2�ɕϊ������B
3�D������]�̑��x2�́A�O���̃G�l���M�[��79.7����1�łł���B
4�D������]�̑��x2�́A���]�̑��x2��79.7�{�ł��B
5�D������]�����G�l���M�[�́A���]�����G�l���M�[��79.7����1�ł��B
6�D���]�����G�l���M�[�́A������]�����G�l���M�[��79.7�{�ł��B
7�D�����O���ŁA�����G�l���M�[�̋O���ł́A������]�̑��x2�́A���]�O���̑��x2��79.7�{�ł��B
���܂ōl���Ă����A�O���̃G�l���M�[�����x2�̎��́A���]�̏ꍇ�̎��ł��B
9�D������]�̏ꍇ�̎��́A
10�D���]�O���̃G�l���M�[���������x2��79.7
�������x2�����]�O���̃G�l���M�[�~79.7�A�ł��B
11�D������]�̃G�l���M�[����ʂ́A���]�̃G�l���M�[����ʂ�79.7����1�ł��B
12�D������]�̃G�l���M�[��������͌��]��79.7�{�ł��B
�T�D�@���]�ł́AbJ�̃G�l���M�[��b2Km�̑��x2�����B������]�ł́AbJ�̃G�l���M�[�͂ǂꂾ���̑��x2����邩�B
�E������]���鑬�x2�����]�O���̃G�l���M�[�̒l�͂ǂ��ł��邩�B
�������r�A1569.32Km��(3.091�~104J)��79.65
���ʂ̘r�A23542Km��(6.954�~104J)��79.68
�傫���r�A3138.72Km��(1.236�~105J)��79.7
���̎�����A������]�̂Ƃ��AbJ�̌��]�O���G�l���M�[�́Ab�~79.7Km�̑��x2�����B
������]�����邽�߂ɁA�O����bJ�̌��]�O���G�l���M�[�́Ab�~79.7K���̑��x2�����B
�܂Ƃ߂ĕ\�Ɏ����B
|
��]�̎�� |
�����x���O���̃G�l���M�[ |
bJ�̃G�l���M�[����鑬�x2 |
�� |
�i�ދ����̊��� |
(�i�ދ����̊���)2 |
|
���] |
�P |
bKm |
���]�O���̃G�l���M�[�����x2 |
0.112 |
1 |
|
������] |
79.7 |
b�~79.7K�� |
���]�O���̃G�l���M�[�����x2��79.7 ���x2�����]�O���̃G�l���M�[�~79.7 |
�P |
79.7 |
�U�D�@�r�̒��S�ɑ��z���ʂ̉��{�̃u���b�N�z�[�������݂��邩�B
�E�u���b�N�z�[���̕\�ʂ̌��q���B
�O���G�l���M�[���\�ʂ̌��q���~�͂����q1�̃G�l���M�[
�\�ʂ̌��q�����O���G�l���M�[���͂����q1�̃G�l���M�[���O���G�l���M�[��10�|20J
���̎�����A
�����Șr�̃u���b�N�z�[���̕\�ʂ̌��q����7.310�~1020J�EKm��10�|20J=7.31�~1040��
���ʂ̘r�̃u���b�N�z�[���̕\�ʂ̌��q����1.645�~1021J�EKm��10�|20J=1.645�~1041��
�傫�Șr�̃u���b�N�z�[���̕\�ʂ̌��q����2.923�~1021J�EKm��10�|20J=2.923�~1041��
�E�u���b�N�z�[���̔��a�ɑ��݂��錴�q���B
�\�ʂ̌��q�����S��2�ł�����Ar�͂����炩�B
�����Șr�A�S��2��7.31�~1040�@��2��7.31�~1040��4��3.14��0.582�~1040��
����0.763�~1020��
���ʂ̘r�A�S��2��1.645�~1041�@��2��16.45�~1040��4��3.14��1.310�~1040��
����1.144�~1020��
�傫�Șr�A�S��2��2.923�~1041�@��2��29.23�~1040��4��3.14��2.327�~1040��
����1.526�~1020��
�E�u���b�N�z�[���̔��a�̑傫���B
���q�̑傫���́A10�|16���ł�����A���a��10�|16m�~���a�̌��q��
�����Șr�A10�|16���~0.763�~1020��7.63�~103m��7.96Km
���ʂ̘r�A10�|16���~1.144�~1020��1.144�~104����11.44Km
�傫���r�A10�|16���~1.526�~1020��1.526�~104����15.26Km
�E�u���b�N�z�[���ɑ��݂��錴�q���B
�u���b�N�z�[���ɑ��݂��錴�q����4��3�~��3�ł��B
�����Șr�A4��3�~�i0.763�~1020�j3��1.860�~1060��
���ʂ̘r�A4��3�~�i1.144�~1020�j3��6.268�~1060��
�傫�Șr�A4��3�~�i1.526�~1020�j3��14.877�~1060��
�E�u���b�N�z�[���̎��ʂ͑��z���ʂ̉��{���B
�u���b�N�z�[���̌��q���͑��z�̌��q���̉��{�������߂�B
���z�̌��q���́A�U�~1026�~1.989�~1030�j����1.1934�~1057�ł��B
�����Șr�A1.860�~1060���i1.1934�~1057�j��1.558�~103�{
���ʂ̘r�A6.268�~1060���i1.1934�~1057�j��5.252�~103�{
�傫�Șr�A14.877�~1060���i1.1934�~1057�j��1.247�~104�{
�����Șr�̒��S�ɑ��z���ʂ�1.558�~103�{�̃u���b�N�z�[�������݂���B
���ʂ̘r�̒��S�ɑ��z���ʂ�5.252�~103�{�̃u���b�N�z�[�������݂���B
�傫�Șr�̒��S�ɑ��z���ʂ�1.247�~104�{�̃u���b�N�z�[�������݂���B
�܂Ƃ߂ĕ\�ɋL���B
|
|
�u���b�N�z�[���̕\�ʂɑ��݂��錴�q�� |
�u���b�N�z�[���̔��a�ɑ��݂��錴�q�� |
�u���b�N�z�[���̔��a�̑傫�� |
�u���b�N�z�[���̌��q�� |
�u���b�N�z�[���͑��z���ʂ̉��{���B |
|
�����Șr�̒��S�̃u���b�N�z�[�� |
7.31�~1040�� |
0.763�~1020�� |
7.96Km |
1.860�~1060�� |
1.558�~103�{ |
|
���ʂ̘r�̒��S�̃u���b�N�z�[�� |
1.645�~1041�� |
1.144�~1020�� |
11.44Km |
6.268�~1060�� |
5.252�~103�{ |
|
�傫�Șr�̒��S�̃u���b�N�z�[�� |
2.923�~1041�� |
1.526�~1020�� |
15.26Km |
14.88�~1060�� |
1.247�~104�{ |
�������̂��Ƃ��A�g�߂ɑ��݂���V�����ƊC�����̉�]����m����B
���V���������z�n�̌��]�O���ɑ��Đ����̕����Ɏ��]���Ă���̂͂ǂ����Ă��B�V���������|���̂܂܌��]���Ă��鎖�̉𖾁B�V�����͂ǂ̂悤�Ɏ��]���Ă��邩�B
�V�����͎��]�������]�ʂɑ���98�x�X���Ă���B���̎��́A�V�����͌��]���ɑ��ė�����]���Ă��邱�Ƃł��B�V�����̌��]���x�́A�b��6.81�j���ł��B
(��͌n�̘r�̐��́A��͌n�̒��S�̃u���b�N�z�[���̉e�����A�����Ƌ߂��r�̒��S�̃u���b�N�z�[���̉e�����邽�߁A�r�̒��S�̃u���b�N�z�[���𒆐S�ɗ�����]���Ă���B
����Ɠ����悤�ɁA�V�����́A���z�̉e�����A�����̒��S�̉e�����Ă���B
�V�����̎��ʂ͒n�����ʂ�14.54�{�ł���A���S�j�̎��ʂ͂قڂ���ɋ߂��B
���S�j�̎��ʂ́A�قڑS�̎��ʂɓ������B(���̎��Ɋւ��āA���́A2008�N9��1���ɒ�o��������2008�|223099�̢������15��ɋL�����B)
�V�����̌��]�̋O���G�l���M�[�����]���x2��6.812�i��46.376�i
�V�����̗�����]���x2�����]���x2�~79.7��46.376Km�~79.7��3696.175Km
�V�����̗�����]���x��(3696.175)1/2Km/s=60.796Km/s
�V�����̗�����]�̋O���G�l���M�[��������]���x2��60.7962�i��3696.175
�V�����͕b��60.796Km�ŗ�����](���])���Ȃ���A���z�̎�����A�b��6.81Km�Ō��]���Ă���B
�V�D�@�V�����͎��]���Ă���̂�������]���Ă���̂��B
���]�̏ꍇ�A1���]�Ői�ދ����͂����炩�B
1�����鋗���́A2����2�~�~�V�����̔��a��2�~3.14�~2.5559�~104Km��1.605�~105Km�ł��B
�V������1���]��������́A0.718���ł��B
�b��60.796Km��0.718�����鋗���́A
60.796Km�~0.718�~24�~60�~60��3.771�~106Km�ł��B
����́A1���]�̉��{�̋������B
3.771�~106Km��(1.605�~105Km)��2.350�~10
1���]��23.5�{�̋����ł��B
����āA�V�����͗�����]���Ȃ��玩�]���Ă���B�@
�W�D�@�V�����̗�����]�̋O���G�l���M�[�͂ǂ̂悤�ɂł��邩�B
(2008�N1��4���ɒ�o��������2008�|23309�̢�������P��ɋL�����A�O���G�l���M�[�́A���q1�̃G�l���M�[�~���q�̐��ł��B����ŁAaJ�́A�o��������q1�̃G�l���M�[�~�o��������q�̐����o��������q1�̃G�l���M�[�~���z�̕\�ʂ̌��q���A�ł��B
aJ�͏o��������q1�̃G�l���M�[�ł��B
��L�̋O���G�l���M�[�͌��]�̋O���G�l���M�[���ǂ̂悤�ɂł��邩�ɂ��Ăł��B
������]�̋O���G�l���M�[�������͓����ł��B
������]�̋O���G�l���M�[��������]���镨�̂̕\�ʂ̌��q���o���d�C�̌��q�̃G�l���M�[��������]���镨�̂̕\�ʂ̌��q���~1�̌��q�����d�C�̌��q1�̃G�l���M�[�ł��B
�X�D�@�V������1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�͂����炩�B
�V�����̕\�ʂ̌��q����6.909�~1035�ł��B(���̎��ɂ��ẮA2008�N10��17���ɒ�o��������2008�|268538�̢�F��11��̢������11��ɋL�����B)
1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�́A
3.691�~103�i��(6.909�~1035��)��5.35�~10�|33�i
1�̌��q�ŁA5.35�~10�|33�i�̓d�C�̌��q�Ǝ��C�̌��q���ł���B
�P�O�D�@�V�����́A���̓d�q�̃��u�̌��]�O���͂����炩�B
1.233�~10�|41�i����(5.35�~10�|33�i)��2.3�~10�|9��
���̓d�q�̃��u�̌��]�O���́A2.3�~10�|9���ł��B
�P�P�D�@�V�����́A���̏�̂`�͂����炩�B(A�͒n�\�̃G�l���M�[��A�{�ł��邱�Ƃ������B�n�\�̓d�q�̃��u�̋O����1.058�~10�|10���A���x���P���Ƃ���B���̎��Ɋւ��ẮA2007�N2��18���ɒ�o��������2007�|67506�̢���͂ƔM��ɋL�����B)
1.058�~10�|10�����`��2.3�~10�|9��
�`��1.058�~10�|10����(2.3�~10�|9��)��4.6�~10�|2
�P�Q�D�@�V�����́A���̏�̉��x�͂����炩�B
���x���`2��(4.6�~10�|2)2��2.116�~10�|3��0.002116(��)
���̏�̉��x�́A0.002116���ł��B
�V�����̕\�ʂ̂P���q�����1�̓d�C�̌��q�̃G�l���M�[�́A5.35�~10�|33�i�ł��B
�V�����̕\�ʂ̓d�q�̃��u�̌��]�O���́A2.3�~10�|9���ŁA���̏�̂`��4.6�~10�|2�ŁA���̏�̉��x�́A0.002116���ł��B
���̒l�́A�V���������z������t�˗ʂ́A�n����1�Ƃ���ƁA0.0027�Ƃقړ������B
�n�����P���Ƃ���ƁA0.0027���ł��B
���̎��ɂ���ė����ł��邱�ƁB
1�D���z������t�˗ʂƓ����G�l���M�[��f���̕\�ʂ̌��q�͍���Ă���B
2�D������]���x2��������]�̋O���G�l���M�[�̍l���͐������B
3�D������]�̋O���̃G�l���M�[���\�ʂ̌��q���~1���q��1���]�ō��d�C�̌��q�⎥�C�̌��q�̃G�l���M�[
���C�����̎��]���͌��]�O���ʂɐ����Ȓ����ɑ���28.8�x�X���Ă��āA���]�����͖�16���Ԃł��B�C�����͂ǂ����Ă��̂悤�ȉ�]�����邩�̉𖾁B�C�����͂ǂ̂悤�Ɏ��]���Ă��邩�B
�P�R�D�@�C�����͎��]���Ă���̂�������]���Ă���̂��B
�C�����́A�V������艓���Ɉʒu���A���z�����G�l���M�[���������A���]���x���x���B���̏�A���ʂ͒n����17.15�{�ŁA�V�������d���B����āA�C�����͎����̒��S�̃G�l���M�[�ŁA������]���Ă���B
���]�̏ꍇ�A1���]�Ői�ދ����͂����炩�B
1�����鋗���́A2����2�~�~�C�����̔��a��2�~3.14�~2.4764�~104Km��1.555�~105Km�ł��B
�C������1���]��������́A0.671���ł��B
�b��48.566Km��0.671�����鋗���́A
48.566Km�~0.671�~24�~60�~60��2.816�~106Km�ł��B
����́A1���]�̉��{�̋������B
2.816�~106Km��(1.555�~105Km)��1.811�~10
1���]��18.11�{�̋����ł��B
����āA�C�����͗�����]���Ȃ��玩�]���Ă���B
�P�S�D�@�C�����́A������]�̋O���G�l���M�[�͂ǂ̂悤�ɂł��邩�B
�C�����̎��ʂ͒n�����ʂ�17.15�{�ł���A���S�j�̎��ʂ͂قڂ���ɋ߂��B
�C�����̌��]�̋O���G�l���M�[�����]���x2��5.442�i��29.594�i
�C�����̗�����]�̋O���G�l���M�[��������]���x2�����]���x2�~79.7��29.5936�i�~79.7��2358.6�i
������]���x��(2358.6)1/2=48.566Km
�C�����̗�����]�̋O���G�l���M�[��������]���x2��48.5662�i��2358.6J
�C�����͕b��48.566Km�ŗ�����](���])���Ȃ���A���z�̎�����A�b��5.44Km�Ō��]���Ă���B
�P�T�D�@�C�����́A1�̌��q��1���]�ō��d�C�̌��q�P�̃G�l���M�[�͂����炩�B
�C�����̕\�ʂ̌��q����6.101�~1035�ł��B
2.359�~103�i��(6.101�~1035��)��3.867�~10�|33�i
1�̌��q��1���]�ō��d�C�̌��q1�̃G�l���M�[��3.867�~10�|33�i�ł��B
�P�U�D�@�C�����́A���̓d�q�̃��u�̌��]�O���͂����炩�B
1.233�~10�|41�i����(3.867�~10�|33�i)��3.189�~10�|9��
���̓d�q�̃��u�̌��]�O���́A3.189�~10�|9���ł��B
�P�V�D�@�C�����́A���̏�̂`�͂����炩�B
�`��1.058�~10�|10����(3.189�~10�|9��)��3.318�~10�|2
���̏�̂`�́A3.318�~10�|2�ł��B
�P�W�D�@�C�����́A���̏�̉��x�͂����炩�B
���x���`2��(3.318�~10�|2)2��1.1�~10�|3��0.0011(��)
���̏�̉��x�́A0.0011���ł��B
�C�����̕\�ʂ̂P���q�����1�̓d�C�̌��q�̃G�l���M�[�́A3.867�~10�|33�i�ł��B
�C�����̕\�ʂ̓d�q�̃��u�̌��]�O���́A3.189�~10�|9���ŁA���̏�̂`��3.318�~10�|2�ŁA���̏�̉��x�́A0.0011���ł��B
���̒l�́A�C���������z������t�˗ʂ͒n����1�Ƃ���ƁA0.0011�Ɠ������B
�n�����P���Ƃ���ƁA0.0011���ł��B
���̎��ɂ���ė����ł��邱�ƁB
1�D���z������t�˗ʂƓ����G�l���M�[��f���̕\�ʂ̌��q�͍���Ă���B
2�D������]���x2��������]�̋O���G�l���M�[�̍l���͐������B
3�D������]�̋O���̃G�l���M�[���\�ʂ̌��q���~1���q��1���]�ō��d�C�̌��q�⎥�C�̌��q�̃G�l���M�[
������܂Ƃ߂ĕ\�Ɏ����B
|
|
���]���x |
���]�O���̃G�l���M�[ |
�����O���̃G�l���M�[ |
������]���x |
�\�ʂ̌��q�� |
1���q��1���]�ō��d�C�̌��q�P�̃G�l���M�[ |
�d�q�̃��u�̌��]�O�� |
���̏�̂` |
���̏�̉��x |
���z�����t�˗� |
|
�V���� |
6.81 |
46.376�i |
3696.175�i |
60.796Km
|
6.909�~1035�� |
5.35�~10�|33�i |
2.3�~10�|9�� |
4.6�~10�|2 |
0.002116�� |
0.0027 |
|
�C���� |
5.44 |
29.594�i |
2358.6�i |
48.566Km |
6.101�~1035�� |
3.867�~10�|33�i |
3.189�~10�|9�� |
3.318�~10�|2 |
0.0011�� |
0.0011 |
���O���G�l���M�[�łł��鑬�x�͂����炩�B���]�̏ꍇ�͂����炩�B������]�̏ꍇ�͂����炩�B������]���x�͌��]���x�̉��{���B���]���x�͗������x�̉��{���B������]�̋O���G�l���M�[�͌��]�̋O���G�l���M�[�̉��{���B���]�̋O���G�l���M�[�͗�����]�̋O���G�l���M�[�̉��{���B
�P�X�D�@���]�̏ꍇ�B
���]�̋O���G�l���M�[(J)�����x2(Km)
���]�O���G�l���M�[����J�Ƃ���ƁA���x2Km����J
���xKm=��1/2J
����āA��J�̋O���G�l���M�[�ł�1/2Km�̌��]���x���ł���B
�Q�O�D�@������]�̏ꍇ�B
������]�̋O���G�l���M�[(J)��������]���x2(Km)�����]���x2�~79.7
������]�̋O���G�l���M�[����J�Ƃ���ƁA������]���x2Km����J
������]���xKm=��1/2J��(���]���x2�~79.7)1/2=���]���x�~8.927
���]���x��������]���x��8.927��������]���x�~0.112
���]���x2��(������]���x�~0.112)2��������]���x2�~0.01254
������]���x2�����]���x2��0.01254�����]���x2�~79.7
���]�̋O���G�l���M�[��������]�̋O���G�l���M�[�~0.01254
������]�̋O���G�l���M�[�����]�̋O���G�l���M�[��0.01254�����]�̋O���G�l���M�[�~79.7
����āA��J�̗�����]�̋O���G�l���M�[�ŁA��1/2Km�̗������x���ł���B
�܂��A������]���x�����]���x�~8.927�B
���]���x��������]���x�~0.112
���]�̋O���G�l���M�[��������]�̋O���G�l���M�[�~0.01254
������]�̋O���G�l���M�[�����]�̋O���G�l���M�[�~79.7
�����\�Ɏ����B
|
|
���] |
������] |
|
���x
|
��J�̋O���G�l���M�[�ŁA ��1/2Km�̑��x���ł���B ������]���x�~0.112 |
PJ�̋O���G�l���M�[�ŁAP1/2Km�̑��x���ł���B ���]���x�~8.927 |
|
���x2 |
������]���x2�~0.01254 |
���]���x2�~79.7 |
|
�O���G�l���M�[ |
������]���x2�~0.01254 ������]�̋O���G�l���M�[�~0.01254 |
���]���x2�~79.7 ���]�̋O���G�l���M�[�~79.7 |
�����̎��ɂ���ė����ł��鎖�B
������]�̏ꍇ�B
���z������t�˗ʂƓ����G�l���M�[��f���̕\�ʂ̌��q�͍���Ă���B���̘f���̕\�ʂ̌��q�����G�l���M�[��������]�̑��x2�ɂȂ��Ă���B
���]�̏ꍇ�B
���z������t�˗ʂƓ����G�l���M�[��f���̕\�ʂ̌��q�͍���Ă���B���̘f���̕\�ʂ̌��q�����G�l���M�[�����]�̑��x2�ɂȂ��Ă���B
�f���̕\�ʂ̓d�q�̃��u�������q1�̃G�l���M�[�����z����͂����q1�̃G�l���M�[(���̎��ɂ��ẮA2008�N10��17���ɒ�o��������268538�̢�F��11��ɋL�����B)
�Ȃ��A
�d�q�̃��u�A�z�q�̃��u�Ɋւ��ẮA2002�N11��7���ɒ�o��������2002�|360006�̢���q�����G�l���M�[�ƈ��͋y�їz�q�A�d�q�̃��J�j�Y���Ƒ傫����ɋL�����B
�d�C�̌��q�Ǝ��C�̌��q�̖��Â��́A2003�N9��29���ɒ�o�����A����2003�|374993�̢�d�C�A���C�A��R��ɋL�����B
��ɁA���l�Ȃ��Ƃ��A
2011�N3���̓��{�V���w��@���A�^�C�g���u�V�����̎��]�������]�ʂɑ���98�x�X���Ă���̂͂Ȃ����B�v�Ƃ��Ă����\�����̂ŁA�L�����d�����Ă���B
2014�N3���̓��{�V���w��Ŕ��\�������B�u��
�^�C�g���u�F���̑f���q�̕K�v�����͉����v
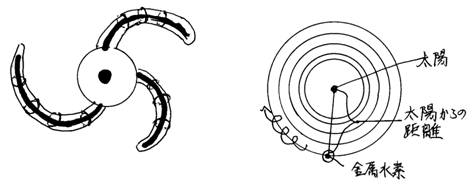
�@�F���ɉ����āA�f���q�̏�Ԃ͂ǂ̂悤�ł��邩�B���̂��Ƃ���A�f���q�͂ǂ̂悤�Ȃ��̂łȂ���Ȃ�Ȃ����A�f���q�̕K�v������m��B�������q���́A���z�̎��ʂ�8�{�ȏ�̐����������Ăł����A���G�l���M�[�̒����������k���Ăł������̂ł��B(���̎�����A�����q����A���v�Z����BA�Ƃ͒n�\�̃G�l���M�[�̉��{���������B)�@���z�̎��ʂ�8�{�̐��̒������̉��x�́A���z�̒�����82�{�ł�����A�����q���̒����̉��x�����z�̒����̉��x�~82�B�����q�����u���b�N�z�[���Ɠ��l��6.353����1�Ɏ��k����Ƃ��܂��B�����q����A2�����z�̒����̉��x�~82�~6.3532�BA2��15�~106�~64�~6.3532�BA=�i15�~106�j1/2�~8�~6.353��1.968�~105�B�����q����A=1.968�~105�@�����z�̎��ʂ��u���b�N�z�[���ɂ���ƁA���a�RKm�ɂȂ�܂��B(���̎�����u���b�N�z�[����A���v�Z����)�@���z�̔��a�͖�70��Km�ł��B�d�́i���L���́j��G��M����2�A���AG=�d�͒萔�A����M���v�X�̎��ʁA�������̊Ԃ̋����B���ʂ͓����ł�����A�d�͂̔�́A���z�F�u���b�N�z�[����32�F�i7�~105�j2��9�F49�~1010���P�F5.444�~1010�B���z�̏d�͂́A�n�\�̏d�͂�10�{�ł�����A�n�\�̏d�́F�u���b�N�z�[���̏d�́��P�F10�~5.444�~1010���P�F5.444�~1011�ł��B����ŁA�u���b�N�z�[����A=�i���́j1/2=�i5.444�~1011�j1/2=7.378�~105�ł��B�u���b�N�z�[����A��7.378�~105�ł��B���r�b�O�o���̈ȑO�̑O���ŁA���̂ŁA�z�q�̃��u�Ɠd�q�̃��u�͎��]�������Ă������A���̂̑傫���͂����炩�B(���̎��Ɋւ��ẮA2010�N3���̓��{�V���w��̍u��a�u�r�b�O�o���̈ȑO�̑傫���ƌ��q���ƈ��́v�Ŕ��\����)�r�b�O�o���̈ȑO�̓d�q�̃��u�̃G�l���M�[���PJ�Ƃ���ƁA�r�b�O�o���̈ȑO�̋��̂̔��a��6.422�~10-5���ł��B�f���q�́A�g�傷��@�\�Ək������@�\�������Ă���B���ꂪ�F���̑f���q�̕K�v�����ł��B���u�̋O���G�l���M�[��8.665�~10-24Jm�����]�O���B
����
�u�����q���Ƒf���q�v
�y�P�z�����q����A�͂����炩�B(A�͒n�\�̃G�l���M�[�̉��{�ł��邩�������܂�)
�������q���́A���z�̎��ʂ�8�{�ȏ�̐����������Ăł����A���G�l���M�[�̒����������k���Ăł������̂ł��B(���̎�����A�����q����A���v�Z����)
���z�̎��ʂ�8�{�̐��̒������̉��x�́A���z�̒����̉��x��82�{�ł�����A
�����q���̒����̉��x�����z�̒����̉��x�~82
�u���b�N�z�[���͒��V�������̂��ƁA6.353����1�Ɏ��k���鎖������܂����B
����ŁA�����q����6.353����1�Ɏ��k����Ƃ��܂��B
�����q����A2�����z�̒����̉��x�~82�~6.3532
A2��15�~106�~64�~6.3532
A=�i15�~106�j1/2�~8�~6.353��1.968�~105
�����q����A=1.968�~105
�����q����A��1.968�~105�ł��B
�y�Q�z�����q���̓d�q�̃��u�̌��]�O���͂����炩�B
�����q���̓d�q�̃��u�̌��]�O�����n�\�̓d�q�̃��u�̌��]�O���������q����A��1.058�~10-10m��(1.968�~105)��5.376�~10-16m�B
�����q���̓d�q�̃��u�̌��]�O���́A�n�\��1.968�~105���̂P�ɒZ�k����Ă���B
�f���q�͒Z�k�����B
����ŁA��Ԃ͒Z�k�����B
�E�����q����A=1.968�~105�A����A�����q���̎��ԁA��ԁA���́A���x�������ł��܂��B
�����q���̎��Ԃ͒n�\�́A1��(1.968�~105)��5.081�~10-6�A�{�ł��B
�����q���̋�Ԃ͒n�\�́A1��(1.968�~105)��5.081�~10-6�A�{�ł��B
�����q���̈��͂͒n�\�́A(1.968�~105)2��3.873�~1010�{�ł��B
�����q���̉��x�́A(1.968�~105)2��3.873�~1010���ł��B
���̎���\�Ɏ����B
�����q���̏��
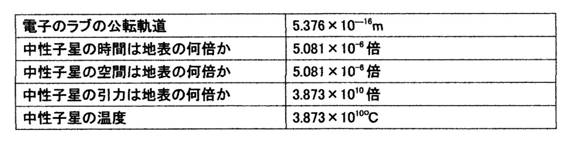
�u�u���b�N�z�[���Ƒf���q�v
�u���b�N�z�[���͂ƂĂ��d�������ł��B
���̎��́A�u���b�N�z�[��������Ă���f���q�́A�����Ԃ��ꂽ��ԂɂȂ��Ă���Ƃ������Ƃł��B
�����Ԃ��ꂽ��ԂƂ͑f���q�͏������Ȃ��Ă���Ƃ������Ƃł��B
�f���q���������Ȃ��Ă���Ƃ́A�f���q�͎��k���Ă���Ƃ������Ƃł��B
�f���q�����k���Ă���Ƃ͑f���q�͎��k�ł���Ƃ������Ƃł��B
�f���q�͎��k�ł�����̂ł���Ƃ������Ƃł��B
���u���b�N�z�[���́A�f���q�͎��k���邱�Ƃ��ؖ����Ă��܂��B
�y�R�z�u���b�N�z�[����A�͂����炩�B
�����z�̎��ʂ��u���b�N�z�[���ɂ���ƁA���a�RKm�ɂȂ�܂��B(���̎�����u���b�N�z�[����A���v�Z����)
���z�̔��a�͖�70��Km�ł��B
�d�́i���L���́j��G��M����2�@�@�@
�A���A�@G=�d�͒萔�A�@����M���v�X�̎��ʁA�@�������̊Ԃ̋����B
���ʂ͓����ł�����A�d�͂̔�́A����2�ɔ���Ⴕ�܂��B
���z�F�u���b�N�z�[����32�F�i7�~105�j2��9�F49�~1010���P�F5.444�~1010
���z�̏d�͂́A�n�\�̏d�͂�10�{�ł�����A
�n�\�̏d�́F�u���b�N�z�[���̏d�́��P�F10�~5.444�~1010���P�F5.444�~1011�ł��B
����ŁA
�u���b�N�z�[����A=�i���́j1/2=�i5.444�~1011�j1/2=54.441/2�~105��7.378�~105
�u���b�N�z�[����A��7.378�~105�ł��B
�y�S�z�u���b�N�z�[���̓d�q�̃��u�̌��]�O���͂����炩�B
�u���b�N�z�[���̓d�q�̃��u�̌��]�O�����n�\�̓d�q�̃��u�̌��]�O�����u���b�N�z�[����A��1.058�~10-10m��(7.378�~105)��1.434�~10-16m�B
�u���b�N�z�[���̓d�q�̃��u�̌��]�O���́A�n�\��7.378�~105���̂P�ɒZ�k����Ă���B
�f���q�͒Z�k�����B
����ŁA��Ԃ͒Z�k�����B
�E�u���b�N�z�[����A=7.378�~105�A����A�u���b�N�z�[���̎��ԁA��ԁA���́A���x�������ł��܂��B
�u���b�N�z�[���̎��Ԃ͒n�\�́A1��(7.378�~105)��1.355�~10-6�A�{�ł��B
�u���b�N�z�[���̋�Ԃ͒n�\�́A1��(7.378�~105)��1.355�~10-6�A�{�ł��B
�u���b�N�z�[���̈��͂͒n�\�́A(7.378�~105)2��5.443�~1011�{�ł��B
�u���b�N�z�[���̉��x�́A(7.378�~105)2��5.443�~1011���ł��B
���̎���\�Ɏ����B
�u���b�N�z�[���̏�ԁB
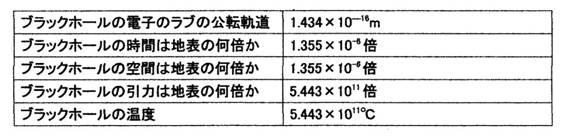
�y�T�z���̒��͂ǂ̂悤�ł��邩�B
�@�@�y�}�z���̒������ŁA�j�Z���������N������̋O���́A10�|10m��(�j�Z���̏��A)��10�|10m��(3.873�~103)=2.582�~10-14m�A�ł��B
���̒������ŁA�����q���ɂȂ��̋O���́A10�|10m��(�����q����A)��10�|10m��(1.968�~105)=5.081�~10-16m�A�ł��B
���̒������ŁA�����q�̊O���̓d�q�̃��u���r�˂���A�z�q�̃��u�ɂȂ��̋O���́A10�|10m��(�u���b�N�z�[����A)��10�|10m��(7.378�~105)=1.355�~10-16m�A�ł��B
�O���̎��k��1.355�~10-16m��(5.081�~10-16m)��0.227(�{)�ł��B
5.081�~10-16m��(1.355�~10-16m)��3.750�B3.750���̂P�ɂȂ�܂����B
�����q�̊O������]���Ă���d�q�̃��u���r�˂���3.750���̂P�ɂȂ�܂����B
���z���ʂ�30�{�̐������V���������N�����Ƃ��ł���u���b�N�z�[���͗z�q�̃��u�ł�����ǂ��A���m�ɕ\������ƁA�����q�̃��u�̊O���̓d�q�̃��u���r�˂��ꂽ�z�q�̃��u�ł��B
�y�����̐����z
�@�P�O �@ ���̒������ŁA�j�Z���������N������̋O���́A10�|10m��(�j�Z���̏��A)��10�|10m��(3.873�~103)=2.582�~10-14m
�@�P�P�@ ���̒������ŁA�����q���ɂȂ��̋O���́A10�|10m��(�����q����A)��10�|10m��(1.968�~105)=5.081�~10-16m
�@�P�Q�@ ���̒������ŁA�����q�̊O���̓d�q�̃��u���r�˂���A�z�q�̃��u�ɂȂ��̋O���́A10�|10m��(�u���b�N�z�[����A)��10�|10m��(7.378�~105)=1.355�~10-16m
�@�P�R �@3.750���̂P�ɂȂ�܂���
�@�P�S�@ ���ꂪ�u���b�N�z�[���ɂȂ�
�y�U�z�r�b�O�o���̈ȑO�̑f���q�͂ǂ̂悤�ł��邩�B
�r�b�O�o���̈ȑO�A���݉F���ɑ��݂���f���q�͑S��1�_�ɑ��݂��Ă��܂����B
�f���q�͓ˑR�p���������Ƃ��A�ˑR�����邱�Ƃ��ł��܂���B
���ݑ��݂���F���S�̂̑f���q�̓r�b�O�o���̈ȑO�ɂ����݂����̂ł��B
�ǂ����āA���ݑ��݂���F���S�̂̑f���q�̓r�b�O�o���̈ȑO�ɂ����݂ł������B
����́A���ݑ��݂���F���S�̂̑f���q�͏������Ȃ��Ă�������ł��B���k���Ă�������ł��B
�����̌����́A�f���q�͎��k���g�傷��A�Ƃ������Ƃ��ؖ����Ă��܂��B
�y�V�z�r�b�O�o���̈ȑO�̑O���ŁA���̂ŁA�z�q�̃��u�Ɠd�q�̃��u�͎��]�������Ă������A���̂̑傫���͂����炩�B�S�Ă̎��C�̌��q�̃G�l���M�[�͂����炩�B���͂͂����炩�B
�����̂��Ƃɂ��ẮA2010�N3���̓��{�V���w��̍u��a�u�r�b�O�o���̈ȑO�̑傫���ƌ��q���ƈ��́v�Ŕ��\���܂����B
�F���S�̂̓d�q�̃��u�̐��Ɨz�q�̃��u�̐������Ƃ��܂��B
���a�ɂ��̓d�q�̃��u�����݂���Ƃ��܂��B
�d�q�̃��u�̃G�l���M�[��aJ�Ƃ��܂��B
aJ�Ƃ��ŕ\���������܂��B�Ȃ��Ȃ�Aa�ɂ��Q��(�F���̌��q��)�͌��܂��Ă��邩��ł��B
�E���̂̑傫���͂����炩�B
4��/3�~��3��2��
��3��2����4��/3��2����4.187
����(2����4.187)1/3
���a�����~���]�O��
�d�q�̃��u�̎��]�O���́A���]�O���~3.14��1���]�̎��]�����]�O���~3.14��(7.96�~107��)��8.665�~10�|24Jm���d�q�̃��u�̃G�l���M�[�~3.14��(7.96�~107��)��3.418�~10�|31 Jm���d�q�̃��u�̃G�l���M�[��3.418�~10�|31m��a
�z�q�̃��u�̎��]�O�������]�O���~3.14��1���]�̎��]�����]�O���~3.14��(4.34�~104��)��8.665�~10�|24Jm��(�d�q�̃��u�̃G�l���M�[�~1836)�~3.14��(4.34�~104��)��3.414�~10�|31 Jm���d�q�̃��u�̃G�l���M�[��3.414�~10�|31m��a
����āA
���a�����~���]�O����(2����4.187)1/3�~���]�O����(2����4.187)1/3�~3.418�~10�|31m��a����1/3��0.47771/3�~3.418�~10�|31m��a����1/3��0.781�~3.418�~10�|31m��a����1/3�~4.376�~10�|31m��a
���̂̔��a�́A��1/3�~4.376�~10�|31m��a�A�ł��B
���̂̑傫���́A2�~��1/3�~4.376�~10�|31m��a�A�ł��B
�E1�b�Ԃɂł��鎥�C�̌��q�̃G�l���M�[�͂����炩�B
1�b�Ԃɂł��鎥�C�̌��q�̃G�l���M�[��1���]�łł��鎥�C�̌��q�̃G�l���M�[�~1�b�Ԃ̌��]����1.233�~10�|41Jm�����]�O���~1�b�Ԃ̌��]����1.233�~10�|41Jm��(8.665�~10�|24Jm���d�q�̃��u�̃G�l���M�[)(7.96�~107)2��9.016�~10�|3�~�d�q�̃��u�̃G�l���M�[��9.016�~10�|3�~aJ
1�b�Ԃɂł��鎥�C�̌��q�̃G�l���M�[�́A9.016�~10�|3�~aJ�A�ł��B
�E�S�Ă̓d�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[�͂����炩�B�S�Ă̗z�q�̃��u����鎥�C�̌��q�̃G�l���M�[�͂����炩�B
�S�Ă̓d�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[��1�b�Ԃɂł��鎥�C�̌��q�̃G�l���M�[�~�d�q�̃��u�̐���9.016�~10�|3�~aJ�~�����S�Ă̗z�q�̃��u����鎥�C�̌��q�̃G�l���M�[
�S�Ă̓d�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[�́A9.016�~10�|3�~aJ�~���A�ł��B
�S�Ă̗z�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[�́A9.016�~10�|3�~aJ�~���A�ł��B
�E���͂͂����炩�B
���̏ꍇ�A�����̗z�q�̃��u�̃R�[�i�[�ƊO���̓d�q�̃��u�̃R�[�i�[�͂������Ă���̂ŁA�����͖��ɂ��Ȃ��Ă��ǂ��B
���́��S�Ă̓d�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[�~�S�Ă̗z�q�̃��u��1�b�Ԃɍ�鎥�C�̌��q�̃G�l���M�[��(9.016�~10�|3�~aJ�~��)2
���͂́A(9.016�~10�|3�~aJ�~��)2�A�ł��B
�����\�Ɏ����B
�r�b�O�o���̈ȑO�̑O���ŁA���̂ŁA�z�q�̃��u�Ɠd�q�̃��u�͎��]�������Ă������̗l�q�B
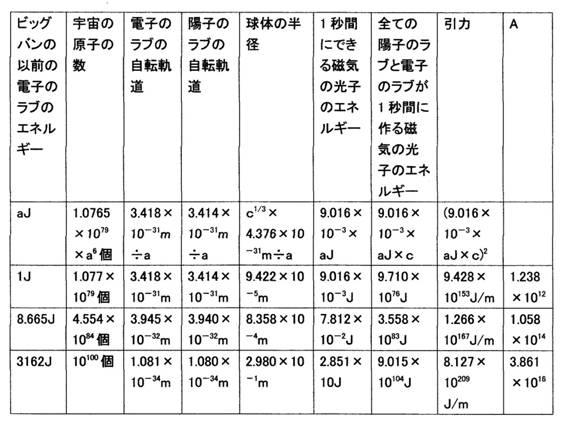
���̂悤�ɁA
�r�b�O�o���̈ȑO�̓d�q�̃��u�̃G�l���M�[��1J�̏ꍇ�A���̂̔��a�́A9.422�~10�|5m�A�ł��B
�r�b�O�o���̈ȑO�̓d�q�̃��u�̃G�l���M�[��8.665J�̏ꍇ�A���̂̔��a�́A8.358�~10�|4m�A�ł��B
�r�b�O�o���̈ȑO�̓d�q�̃��u�̃G�l���M�[��3162J�̏ꍇ�A���̂̔��a�́A2.980�~10�|1m�A�ł��B